ДЗ / семестр4 / БДЗ 3

БДЗ №3

по специальным разделам математического анализа

Выполнил:

Студент группы МП-26

Пузырев Д. В.

Проверил:

Хахалин С. Я.

Оценка:____________________________

Подпись преподавателя:____________________________

Задание 1: Найти оригиналы следующих изображений

а).

Можно восстановить оригинал с помощью функции маткада

А теперь восстановим его честно. 

Сначала разложим дробь на сумму простейших.

И теперь преобразуем это уравнение к сумме членов вида

, чтобы можно было использовать изображение для exp(at)

Для этого приведем первое слагаемое к нужному виду:

Подставив в первоначальное выражение, получим:

Теперь по теореме о дифференцировании изображения и используя изображение для exp(at) получим:

Под f(t) имеется в виду f(t)*η(t)!

Эта функция удовлетворяет всем 3-м условиям, необходимым, чтобы быть оригиналом F(p):

1) f(t)=0, при t<0;

2) Существуют такие М и σ (M>3/4; σ≥3), что

f(t)<M*exp(σ*t)

3) Функция не имеет точек разрыва на любом конечном отрезке [0,T]

Показатель роста функции f(t): σ₀=3

Т.е. F(p) является изображением функции f(t) при Re(p)>3

б).

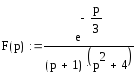
Можно восстановить оригинал с помощью функции маткада

А теперь опять восстановим его честно.

Получим оригинал по второй теореме разложения.

Изображение F(p) есть функция однозначная и имеет лишь конечное количество особых точек, лежащих в конечной части плоскости(-1,-2i,2i)

Это значит, что мы можем применить вторую теорему разложения.

Изображение имеет особые точки +2i, -2i, -1,

∞- нас не интересует, т.к. нам нужны только особые точки, лежащие в конечной части плоскости.

Определение 1: Функция f(z) называется аналитической функцией в области g, если она дифференцируемая во всех точках zg и ее производная непрерывна в этой области

Определение 2: Точка z называется изолированной особой точкой функции f(z), если f(z) – однозначная аналитическая функция в кольце 0<|z-z0|<R, a z0 – особая точка.

Исследуем функцию F(p) на Аналитичность:

Найдем ее производную:

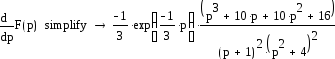
Ее непрерывность нарушается только в особых точках: +2i,-2i, -1 и предел во всех точках кроме этих равен ее значению.

Значит функция аналитична на всей плоскости, кроме этих точек.

Значит точки +2i, -2i, -1 - изолированные особые точки.

Теперь найдем предел функции в каждой из этих точек:

Значит эти точки – существенно особые

Найдем вычеты в этих точках от функции: e^ptF(p)

Для этого найдем коэффициенты c_-1 разложения в ряд Лорана функции F(p) в данных точках, получим:

Т.е. вычеты в этих точках равны:

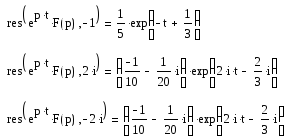
Тогда по второй теореме разложения оригинал равен:

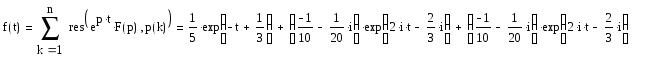
Под f(t) имеется в виду f(t)*η(t)!

Эта функция удовлетворяет всем 3-м условиям, необходимым, чтобы быть оригиналом F(p):

1) f(t)=0, при t<0;

2) Существуют такие М и σ (M=1; σ=0), что

f(t)<M*exp(σ*t)

3) Функция не имеет точек разрыва на любом конечном отрезке [0,T]

(кроме точки 0)

Показатель роста функции f(t): σ₀=0

Т.е. F(p) является изображением функции f(t) при Re(p)>0

Задание 2: Найти изображение функции:

а). Преобразованием Лапласа функции f(t) (которая, вообще говоря, может принимать и комплексные значения), называется функция F(p) комплексной переменной p, определяемая следующим равенством:

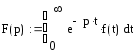
Оригиналом называется всякая функция, удовлетворяющая следующим условиям:

• f(t)=0 при t<0, причем принимается, что f(0)=f(0+0)

• существуют такие постоянные M и σ, что |f(t)|<Me^σt

• На любом конечном отрезке [0;T] функция может иметь лишь конечное число точек разрыва, причем только первого рода.

Наша функция удовлетворяет всем условиям, чтобы быть оригиналом.

(Она =0 при t<0. M>2e², σ₀=0. на любом конечном отрезке [0,T] она имеет не больше 1 точки разрыва: 2)

Если f(t) – оригинал, то стоящий в правой части равенства интеграл Лапласа сходится абсолютно и равномерно в полуплоскости Re p≥σ>σ₀

и называется изображением функции f(t).

Найдем изображение по определению (через интеграл Лапласа):

б).

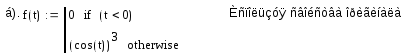
Наша функция удовлетворяет всем условиям, чтобы быть оригиналом.

(Она =0 при t<0. M>1, σ₀=0. на любом конечном отрезке [0,T] она имеет 1 точку разрыва: 0)

Найдем изображение cos³(t).

Имеем по формуле Эйлера:

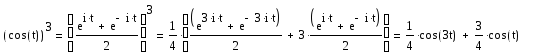
Тогда, используя свойство линейности и формулу для изображения cos(bt)

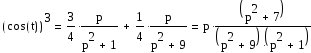
Задание 3: Методом операционного исчисления решить дифференциальное уравнение при заданных начальных условиях:

Пусть x(t)=X(p), тогда:

По таблице изображений находим:

и операторное уравнение имеет вид:

отыщем оригинал:

Теперь для проверки найдем его первые две производные:

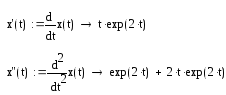
Тогда, подставив t=0 в x(t) и x`(t), получим:

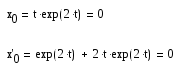
Что совпадает с начальными условиями, теперь составим из производных левую часть уравнения и убедимся, что получим эквивалент начального дифференциального уравнения:

Что доказывает верность решения.