10 блок_ Шуляков_планирование эксперимента / (010) / Методы многомерного поиска экстремума

Методы многомерного поиска экстремума

Все методы поиска экстремума на 2-м этапе подразделяются на градиентные и неградиентные.

Классификация методов поиска

Градиентныеметодыпоискаэкстремума.

1. Градиентный метод.

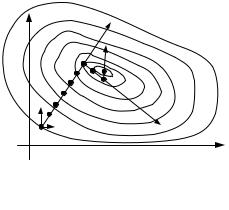
Рассмотрим кривые равного уровня поверхности отклика для функции двух переменных.

Пусть экстремум существует в точке X * . Если попытаться попасть в окрестность этой точки из начальной точки X0 с помощью одного из методов однофакторного анализа (одномерного поиска), то мы

где i , j , k - единичные векторы в направлении координатных осей. Тогда любая точка X m 1 выбирается из условия:

2. Метод крутого восхождения

Одним из вариантов градиентного метода является метод крутого восхождения (ищется максимум). Пусть X0 x10 , x20 ,..., xn0 - начальная точка. Вектор-градиент в этой точке

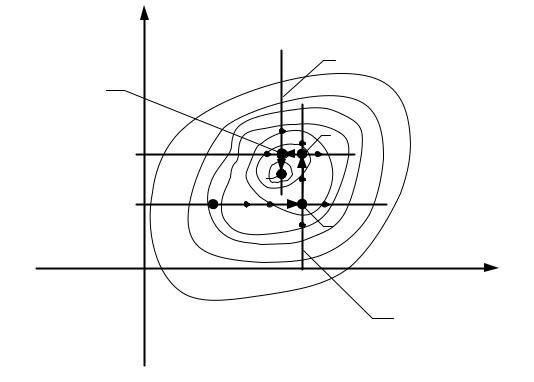
функции в этой точке будет направлением наибыстрейшего возрастания функции.

Как видно из рисунка точка X0 не является стационарной. Сделаем некоторый первый шаг в направлении градиента. Координаты новой точки X x1, x2 ,..., xn определяются из выражения:

где 0 - параметр шага.

xi0 xi xi0 .

Выражение (*) представляет собой уравнение луча.

последний элемент является точкой максимума.

Таким образом, в методе крутого восхождения параметр m

решения одномерной задачи максимизации:

max f X m f X m , где 0

Неградиентные методы поиска экстремума

Метод Гаусса – Зейделя

В основе метода Гаусса – Зейделя лежит идея координатного поиска: ищется частный экстремум при изменении одного из факторов. Пусть из n переменных x1 , x2 ,…,

xn выбрана какая – то одна xq , а значения всех остальных зафиксированы, т.е. определена прямая, параллельная одной из осей, а именно оси xq . Поиск производится вдоль этой

прямой в пределах области эксперимента (т.е. одномерный поиск). Пусть в начале экспериментаx2 const . Поиск ведется вдоль оси x1 . В результате становится возможным

поиск вдоль прямой x13 , т.е. находится значение x2* x22 . Далее фиксируется x22 const и т.д.

В данном методе одна и та же переменная может быть исследована не один раз. Достоинства:

1.Простота процедуры и отсутствие локальных исследований окрестностей опорных точек;

2.Использование методов одномерного поиска.

Недостаток:

1.Ограничение возможности применения: метод применим, когда переменные x1 , x2 ,…, xn - независимы;

2.Нет гребней.

Всвязи с этим возможно осложнение, возникающее на практике. Предположим, что

первая серия опытов привела к отысканию частного экстремума x1* , а попытка сделать следующий шаг будет неудачной, какая бы переменная не выбиралась – улучшить значение y - не удается, хотя известно, что x1* не есть глобальный экстремум x* .

Множество точек, из которых невозможно продолжить процедуру Гаусса – Зейделя называется гребнем.

Метод симплекса

Симплекс – это фигура с n 1 вершинами, с помощью которой формализуется

процедура поиска следующей точки при эффективном движении к экстремуму. Если фигура имеет равные ребра, то она называется однородной, если разные - то неоднородной.

Перевернем симплекс относительно прямой 1-3, противоположной вершине y2 min , получим точку 4 с координатами x14 , x24 . В результате чего получим:

2)y1 , y3 , y4 , среди них y1 min yi , тогда

3)y3 , y4 , y5 , среди них y3 min yi , т.е симплекс совершает вращательно

поступательное движение в направлении экстремума.

Признаком достижения экстремума является или 1. Вращение симплекса вокруг одной вершины

или 2. Повторение симплекса (качание относительно

одного ребра). Точка вращения является наиболее близкой к экстремуму. В случае повторения симплекса вносят изменение в процедуру повторения:

исключают не точку yl min , а точку y l 1 , т.е. предыдущую. Если это не дает результата, то исключают точку y l 2 или изменяют размер симплекса.

Точность определения экстремума: Rz n 1 1 z ,

где z - размер ребра симплекса, т.е. разрешающей способностью (для n 2 Rz 13 z ).