10 блок_ Шуляков_планирование эксперимента / (020) / Активные стратегии одномерного поиска

Активные стратегии одномерного поиска

Пассивные стратегии предполагают для нахождения x*, y* выбор сразу всех N значений х (т.е. N измерений), что является недостатком. С этой точки зрения всякая стратегия, предусматривающая последовательное (пошаговое) проведение опытов, является более прогрессивной, т.к. позво- ляет экономить время и средства (число измерений). Это так называемые активные стратегии.

Далее рассмотрены следующие одномерные активные методы поис- ка экстремума:

∙последовательной дихотомии (половинного деления);

∙чисел Фибоначчи;

∙золотого сечения;

∙поиска по дискретным точкам.

Метод последовательной дихотомии

Идея метода состоит в следующем: из N экспериментов выбираются два (х1, х2) и размещаются на единичном отрезке [0,1] наилучшим образом,

т.е. симметрично относительно середины на расстоянии ±ε 2 , где ε имеет

смысл разрешающей способности, а стратегии, основанные на использова- нии этого параметра, называются ε-минимаксными. В результате сравне- ния y1 и y2 становится возможным указать гарантированный интервал не-

ленности положим, что он смещен влево, т.е. y1 > y2 (рис. 1).

Рис. 1. Реализация метода последовательной дихотомии

Получив таким образом интервал L2(1) , можно повторить к нему

всю описанную процедуру, используя для этого вторую пару (х3, х4). Это даст новый интервал неопределенности:

2

L2(2) = (L2(1) + ε) 2 = (1+ 3ε) 4 .

Затем используется пара (х5, х6). Она позволяет получить

L2(3) = (L2(2) + ε) 2 = (1+ 7ε )8

и т.д. Процесс продолжается до тех пор, пока не будут проведены два по- следних эксперимента (хN-1, хN). Длина оставшегося интервала неопреде- ленности, характеризующая эффективность метода

Особенностью процедуры является то, что эффективность использо- вания очередной пары экспериментов снижается.

например, для пары с номером К:

игрыш → 0 . Хотя теоретически возможность размещения новых пар то- чек сохраняется всегда, практически не имеет смысла использовать более

7…8 пар.

Особенности метода дихотомии:

∙число экспериментов в методе дихотомии меньше числа экспери- ментов в пассивных методах не менее чем в два раза (от 2-х и более: 10, 20, … 40 раз) – это зависит от N и ε;

∙эффективность метода дихотомии снижается с увеличением ε.

3

Метод чисел Фибоначчи

Идея метода: для уменьшения количества измерений в каждом опыте проводится не два измерения (как в методе дихотомии), а только одно. А в качестве второго измерения предполагается использовать предыдущее.

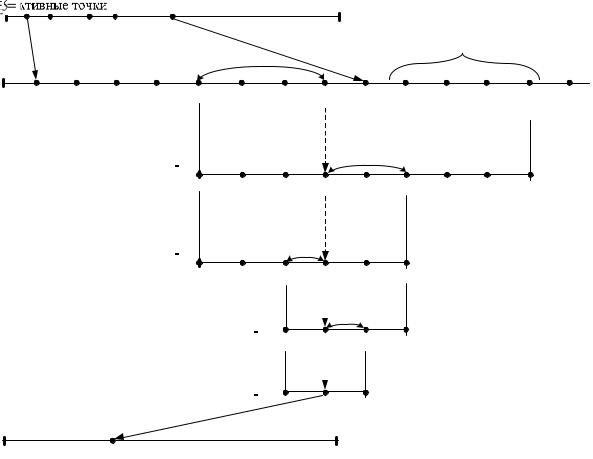
Рассмотрим схему построения алгоритма (рис. 2). Каждое предыду- щее измерение используется как априорно известное на следующем шаге. При этом последний интервал неопределенности:

Рис. 2. Реализация метода чисел Фибоначчи

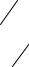
4

Составим таблицу интервалов (здесь i – номер интервала, Li – длина i-го интервала):

Коэффициенты при LN и ε составляют последовательности чисел Фибоначчи (см. таблицу):

Тогда общее соотношение:

Li = FN −i+1LN - FN −i−1ε .

Запишем его для первого интервала L1:

L1 = FN LN - FN −2ε .

Но L1=1 – есть исходный (нормированный) интервал неопределен- ности, поэтому отсюда получается:

Последнее соотношение позволяет оценить эффективность метода чисел Фибоначчи, в первую очередь, по сравнению с методом дихотомии.

Эффективность метода дихотомии:

Исследование последней зависимости показывает, что число измере-

ний в методе дихотомии ненамного превышает число измерений в методе чисел Фибоначчи. (например, при N=5, ε=0,05, NД=7).

Эффективность метода чисел Фибоначчи связана с тем, что сокра- щение длины очередного интервала Li требует проведения только одного нового измерения, в то время, как в методе дихотомии их требовалось бы

2.

Выбор первой экспериментальной точки x1:

x1 =1- L2 ,

зволяет изменить N после начала эксперимента. Желательно же распола- гать стратегией, не требующей предварительного задания N, но по своей эффективности приближающейся к методу чисел Фибоначчи.

7

LN ³ 12 (LN −1 + ε ) .

Сравним результаты метода золотого сечения и метода чисел Фибоначчи.

Это отношение принимает наибольшие значения при ε=0, причем, начиная

L

с N=4 это отношение стабилизируется на уровне N3 LNF =1,17 . Следова-

тельно, с точки зрения эффективности метод золотого сечения занимает промежуточное положение между методами дихотомии и чисел Фибонач- чи.

Преимущество: не надо заранее определять N.

8

Метод пошагового поиска

(Поиск по дискретным точкам)

Рассмотренные активные стратегии поиска экстремума применимы в тех случаях, когда х может принимать любые значения на интервале [0, 1]. Если же х может принимать только определенные дискретные значения, или х может быть только целым числом, то используется Метод пошагово- го поиска (МПШ).

Такая же постановка вопроса возникает и при наличии у функции дисперсии воспроизводимости.

Поиск по дискретным точкам является активной стратегией.

Пусть х принимает какие-то значения х1, х2, … ,хМ* на интервале [0, 1], причем число их конечно. Нумерация этих значений дается в порядке возрастания х. Введем новую переменную z, которая может принимать только целые значения: 1, 2, 3,…М*.

Номера точек на оси х совпадают с первыми М* значениями величи- ны z, поэтому можно поставить в однозначное соответствие этим значени-

_______

ям z величины yz (где z =1, M *), которые будут найдены в точках хz.

Другими словами можно перейти от рассмотрения функции y = f (x) к функции yz = fz (z) .

Будем считать, что для решения задачи поиска в этих условиях ис- пользуется метод чисел Фибоначчи. Отметим на оси z ряд точек с коорди- натами М*+1, М*+2,…,М, выбрав их количество М-М* так, чтобы число М+1 оказалось ближайшим к числу М* числом Фибоначчи (в частном слу- чае может оказаться, что М=М*). Значения yz в этих точках не определя- ются, поэтому сами точки М*+1, М*+2,…,М называются фиктивными.

Таким образом, приходим к задаче:

На оси z задан интервал М+1=Fk, содержащий М целочисленных по-

_____

ложительных значений z ( z =1, M ), и требуется среди первых М* точек z найти такую, в которой yz достигает максимума.

9

Решить задачу можно, если в общих формулах:

Положить ε=0, N=k.

Начнем с выбора первой точки z1. Она определяется равенством: z1 = (1- L2 )Fk . Это равенство учитывает имевшее место при переходе от х к z увеличение интервала [0, 1] → [0, Fk].

Обращаясь к выражению L2 и полагая ε=0, получаем z1 = Fk - Fk −1

(при N=k):

В силу целочисленности Fk и Fk-1 найденное значение z1 будет тоже целочисленным, поэтому точка z1 и симметричная ей z2 займут те положе- ния на оси z, которые допустимы по условиям задачи. При этом длина но- вого интервала неопределенности составит Fk-1. Затем точка z3, симмет- ричная z1 в интервале Fk-1 займет допустимое положение и т.д. Наконец, по

окончании всех экспериментов останется интервал неопределенности

шее (сверху) к М* число Фибоначчи F6=13; следовательно k=6; целочис- ленный параметр z={0…13}.

10

х*=1/3; у*=у(1/3)=0,0645.

Из соображений симметрии выбираем z2=8. Вычисляем значения функции y1 = f (x5 ) = 0,0466 ; y2 = f (x8 ) = 0,0645 .

Положим, что у2>у1 и для дальнейшего рассмотрения остается ин- тервал [5, 13].

2)На интервале [5, 13] сохраняется точка z2, симметрично выбирает- ся z3=10, но z3=10 фиктивная точка, в которой функция не определена, по- этому интервал [10, 13] – отбрасывается, а остается [5, 10].

3)В оставшемся интервале [5, 10] присутствует точка z2=8 и сим- метричная ей z4=7. Из сравнения у4=у(х7)=0,0418 и у2=0,0645 следует, что z* [7,10] .

4)В интервале [7, 10] определена z2 и симметричная ей z5=9. Вычис- ляем у5=у(х9)=0,0542. Остается исследовать интервал [7, 9]. В разрешен- ных точках этого интервала все значения функции известны:

y(x7 ) = 0,0418, y(x8 ) = 0,0645 , y(x9 ) = 0,0542 .

Вывод: z* [8,9] – более точно в рамках условий данной задачи оп- ределить нельзя. Поэтому принимаем: х*≈1/3, у*=у(1/3)=0,0645.