For Exam / Метод интегрирования по частям

§ 3. МЕТОД ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ

Пусть u и v - непрерывно дифференцируемые функции.

С помощью данной формулы вычисление исходного интеграла сводится к вычислению другого интеграла, который может оказаться более простым, чем исходный, или даже табличным. При применении формулы интегрирования по частям подынтегральное выражение представляют в виде произведения двух множителей u и dv . При этом через u обычно обозначают функцию, производная которой проще, чем сама функция u. В частности, через u обозначают многочлен, если под интегралом стоит

произведение многочлена на одну из функций a x , e x , sin x,

cos x. В случае когда под интегралом стоят логарифмическая функция или одна из обратных тригонометрических функций: arcsin x, arccosx, arctgx , arcctgx , то их и обозначают через u.

Иногда формулу интегрирования по частям приходится применять несколько раз.

Пример 1.3. x 3 cos2xdx.

Решение. Введем обозначения u x 3, dv cos2xdx. Для применения формулы интегрирования по частям требуется найти

cos2x C . 4

В дальнейшем решение будем записывать кратко:

x2 x 1ex 2x 1 exdx.

После применения формулы (3.1) степень многочлена под интегралом понизилась. Чтобы многочлен под знаком интеграла “исчез”, применим формулу интегрирования по частям еще раз:

Пример 4.3. arctgxdx.

Решение.

Пример 5.3. I 2 x2 dx.

Решение.

Таким образом, I x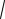2 x2 I 2ln x 2 x2 .

I 1 x2 x2 ln x 2 x2 С .

2