Задача "перераспределения" выводов модуля

Указанная задача возникает перед началом трассировки и решается с целью дополнительного сокращения длины соединений "внутри" модуля (на МКП) и уменьшения числа возможных пересечений печатных проводников.

Для модуля такое перераспределение осуществляется внутри групп эквивалентных выводов (если таковые имеются в модуле), которые соответствуют логически эквивалентным входам функциональных элементов ячейки.

Различаются четыре вида эквивалентности ячеек:

1. Инвариантность входов функциональных элементов

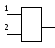
Рис. Входы 1 и 2 эквивалентны.

2. Инвариантность групп входов ячейки

На Рис. Входы (1 2) эквивалентны входам (3 4). (Например, для логических ИМС 2И-НЕ)

3. Инвариантность секций внутри модуля (Например, для ИМС – эквивалентность логических вентилей).

4. Инвариантность ячеек схемы (Для ИМС – одинаковые ИМС).

Первые два уровня эквивалентности можно учесть непосредственно в процессе трассировки связей.

На промежуточном этапе между размещением и трассировкой следует учитывать эквивалентность секций внутри модуля (третий вид эквивалентности).

Отметим, что эквивалентность ИМС учитывается на этапе размещения модулей на МКП. Методы решения задачи является аналогичными для всех видов инвариантности.

Исходными данными при решении задачи являются:

- множество эквивалентных секций в схеме ячейки,

- множество контактов одной секции, имеющие эквиваленты в другой аналогичной секции заданной ячейки,

- "матрица эквивалентности" секций в ячейке ||C_ij||_NxM, где C_ij – номер j- того контакта i- той секции из группы эквивалентных секций,

- N – число секций, входящих в группу одной эквивалентности.

Пример.

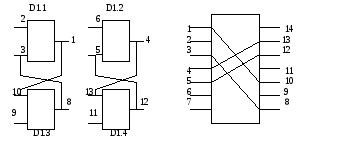
В начальном варианте "внутренняя" трассировка соединений дает четыре потенциальных пересечения трасс.

Учитывая эквивалентность всех четырех секций, входящих в схему ячейки, можно осуществить "перестановку" двух секций с целью ликвидации указанных пересечений.

Для этой цели поменяем местами секции D 1.1 и D 1.2.

Результат "перестановки" секций показан на Рис.

Все пересечения ликвидированы.

Подсчет изменения суммарной длины связей в итерационных алгоритмах

Эта процедура является общей для всех итерационных алгоритмов.

Исходные данные:

Задана модель 1 и матрица расстояний между посадочными местами, т.е.

R = ||r_ij|| и D = ||d_ij||

Требуется: подсчитать изменение числа связей при перестановке местами двух модулей.

Решение:

Если r_ij – число связей между модулями, d_ij – расстояние между ними на МКП, то суммарная длина связей между x_i и x_j равна L_ij = r_ij * d_ij.

Суммарная длина связей между x_i и другими модулями схемы равна

L_i = r_ij*d_ij

Суммарная длина связей в схеме равна

L = r_ij*d_ij

Суммарная длина связей двух указанных модулей со всеми остальными равна

L_ij = L_i + L_j – r_ij*d_ij = r_is*d_is + r_js * d_js – r_ij*d_ij =

= {( r_is*d_is + r_js * d_js)} – r_ij * d_ij (1)

При перестановке модулей местами суммарная длина связей модулей запишется в виде:

L_ji= {( r_js*d_is + r_is * d_js)} – r_ij * d_ij (2)

т.к. расстояния между позициями модулей остаются прежними.

Вычитая (1) из (2) можно вычислить изменение суммарной длины связей при обмене двух модулей местами установки.

∆L_ij = L_ji – L_ij = (r_js – r_is) * (d_js – d_is)

Об эффективности алгоритмов размещения

Критериями оценки эффективности алгоритмов является точность решения задачи (оценивается по результатам трассировки или, перед трассировкой) - по минимуму суммарной длины связей). Этот критерий можно использовать только для задач определенного класса.

Имеющиеся статистические данные показывают, что:

- последовательные алгоритмы имеют невысокую точность по сравнению с итерационными, и эта точность ухудшается с увеличением размерности задачи размещения,

- итерационные алгоритмы более эффективны. Причем более предпочтительными являются алгоритмы парных и групповых перестановок.