6.5. Анализ чувствительности решения к изменению коэффициентов целевой функции

Анализ чувствительности к изменению коэффициентов целевой функции c_jпредполагает определение пределов изменения этих коэффициентов при условии неизменности полученного оптимального решения.

При исследовании на чувствительность решения к изменению коэффициентов целевой функции c_jпрямой задачи удобно воспользоваться решением двойственной задачи. Для двойственной задачи конечная симплекс-таблица в матричном виде может быть записана:, (6.21)

где [Y_B] – матрица-столбец базисных переменных конечной симплекс-таблицы двойственной задачи;

[P^*] – матрица перехода базисных переменных конечной симплекс-таблицы двойственной задачи;

- матрица-столбец исходных коэффициентов целевой функции прямой задачи (в двойственной задаче они играют роль правых частей ограничений);

[C] - матрица-столбец конечных значений коэффициентовc_jдвойственной задачи (для прямой задачи это конечное значение коэффициентов целевой функции).

Аналогично рассмотренному ранее вводится понятие вектора устойчивости оптимального решения двойственной задачи к коэффициентам c_j:

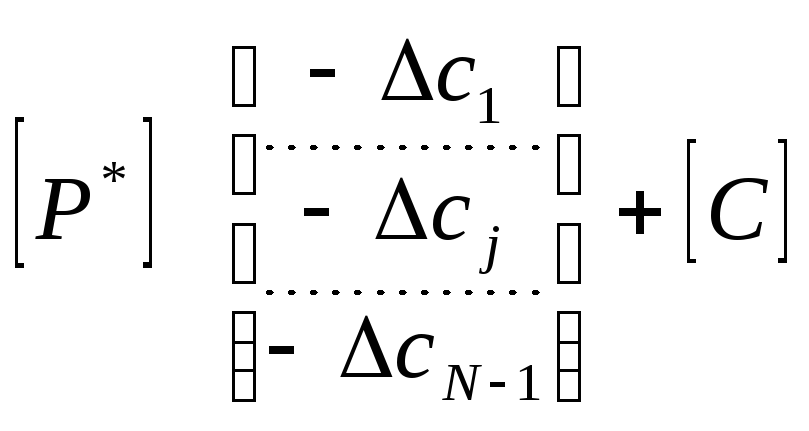. (6.22)

Для исследования на чувствительность решения к изменению коэффициентов c_j исходят из следующих соображений: значения приращенийc_jкак компонент вектора устойчивости [C] должны иметь знак, соответствующий оптимальным коэффициентам в строке целевой функции последней симплекс-таблицы (иначе решение станет уже не оптимальным).

Вектор устойчивости коэффициентов c_jможет быть записан через матрицу преобразования двойственной задачи [P^*] в виде

. (6.23)

Условие неотрицательности для компонент вектора-столбца [C], аналогично рассмотренному [B], может быть представлено в виде системы:

(6.24)

Анализ этой системы легко осуществить отдельно для изменения каждого коэффициентаc_j. Пределы изменения коэффициентаc_jпри переменнойx_j, оказавшейся в последней симплекс-таблицепрямойзадачи в числе свободных, определяются непосредственно коэффициентом в строке целевой функции этой переменной (например,с₁57/4 из симплекс-таблицы прямой задачи означает, что изменениес₁на величинус₁57/4 не приводит к изменению как оптимального решения, так и целевой функции).

Изменение коэффициентов при переменных, оказавшихся в числе базисныхпоследней симплекс-таблицы, приводит к изменению целевой функции.

Например, с₂ис₃прих₂их₃, приращенияс₂ис₃приведут к изменению целевой функции на величинуF =с₂x₂+с₃x₃. При сохранении неизменным полученного оптимального решения х₂=const,x₃=const.

При одновременном изменении нескольких коэффициентов решается система неравенств.

7. Решение транспортных и сетевых задач

7.1. Транспортная задача открытого типа

В общем виде транспортная задача формулируется в следующем виде.

Заданы m пунктов отправления с запасами грузов , n пунктов потребления подали заявки на груз в количестве , известна стоимость перевозки единицы грузаизi-го пункта отправления в j-й пункт назначения. Вводятся переменные, определяющие количество отправляемых грузов из i-го склада в j-й пункт потребления, – x_ij.

Ставится задача минимизировать стоимость перевозок, поэтому целевая функция будет

. (7.1)

Количество груза, отправляемого с каждого склада, не должно превышать имеющихся запасов:

. (7.2)

Условие выполнения заявок каждого пункта потребления запишется в виде

. (7.3)

При равенстве количества запасов и заявок пунктов потребления, т.е.

, (7.4)

задача называется сбалансированной. В случае если заявок больше или меньше запасов, транспортная задача называется открытой (несбалансированной). Решение таких задач возможно путем введения дополнительных условий. Рассматриваются два случая.

1. Если запасы больше потребностей: , то для сведения этой задачи к сбалансированной задаче вводится фиктивный пункт назначения с потребностями

(7.5)

и допущением, что стоимость перевозки единицы груза между любым пунктом i и фиктивным пунктом равна нулю, т.е. c_i(n+1) = 0, i=.

Очевидно, что оптимальное решение такой задачи будет оптимальным и для исходной.

2. Когда запасы меньше потребностей удовлетворение всех пунктов в этом случае невозможно, поэтому необходимо управлять транспортировкой таким образом, чтобы наиболее важные пункты удовлетворялись полнее и чтобы стоимость перевозок была бы минимальной.

Обозначим: r_j – величина ущерба на одну единицу груза в результате невыполнения запроса j-го пункта. Тогда для приведения этой задачи к основной вводится фиктивный пункт отправления А_m+1 с запасами

(7.6)

и предполагается, что стоимость перевозки единицы груза между этим пунктом и любым пунктом назначения равна нулю, т.е. c_(m+1)j = 0 для всех j=.

Далее минимизируем затраты

, (7.7)

где y_j – количество груза, «недовезенного» в пункт j при тех же ограничениях и дополнительном условии

. (7.8)