
Физ.-стат. основы кв. инф.- Богданов (конспект лекций)
.pdf
Рассмотрим для примера четвертую из представленных
выше функций: f (0) =1, f (1) = 0. Нетрудно видеть,
что рассматриваемая функция задает следующее преобразование:
0,0 → 0,0 f (0) = 0,1
0,1 → 0,1 f (0) = 0,1 1 = 0,0 1,0 → 1,0 f (1) = 1,0
1,1 → 1,1 f (1) = 1,1
Задача 5.3.1 Покажите, что введенное выше определение квантовой реализации функции задает унитарное преобразование входного состояния в выходное. Найдите соответствующие унитарные матрицы для каждой из четырех представленных выше функций.
Принцип суперпозиции позволяет подавать на вход схемы квантового вычисления функций не только
определенное базисное состояние x , но и произвольную
суперпозицию таких состояний. Эта возможность обеспечивает так называемый квантовый параллелизм, которой означает, что (в определенном смысле) квантовый
алгоритм позволяет вычислять функцию f (x) для многих
131
значений аргумента x одновременно. Квантовый
параллелизм, таким образом, обеспечивает принципиально важное преимущество квантовых схем вычислений над классическими. Заметим, в то же время, что результаты квантовых параллельных вычислений не могут быть непосредственно экстрагированы из квантовой системы изза неизбежной редукции квантового состояния при измерениях.
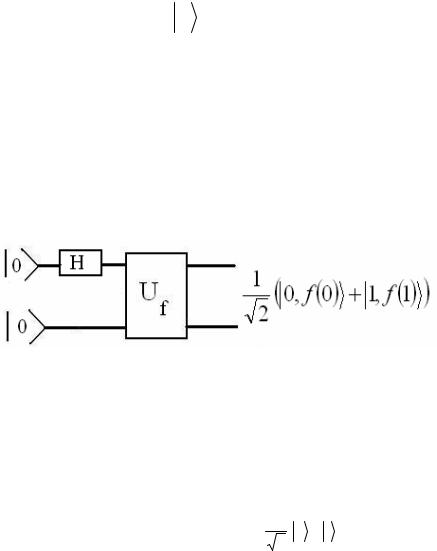
Задача 5.3.2. Докажите справедливость результата, представленного на следующем рисунке.
Рис. 5.3.2 Демонстрация квантового параллелизма для функции с однокубитовой областью определения.
Результаты, полученные в задаче, являются
простейшей |
демонстрацией |
свойства |
квантового |
|||
параллелизма. Благодаря действию элемента Адамара H |
||||||
на первый |
кубит, на вход вычислителя функции |
Uf |
||||
поступает суперпозиция |
состояний |
1 (0 |
+ 1 ). В |
итоге, |
||
|
|
|
|
2 |
|
|
выходное |
состояние |
системы |
|
представляет |
собой |
|
132
суперпозицию результатов вычислений при значениях
аргумента x = 0 и x =1.
Представленный результат может быть обобщен на вычисление функции f (x) с n - битовой областью
определения и 1- битовым множеством значений. |
||||
Квантовая реализация функции |
f (x) |
в этом случае |
||
определяется |
тем |
же |
|
преобразованием |
f |
f (x) , |
|
|
|
x, y → x, y |
где |
символ |
означает |
|
сложение по модулю 2, но теперь |
x - не один кубит, а n - |
|||
кубитовый регистр данных. |
|
|
|
|
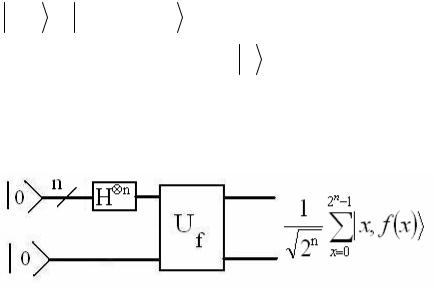
Задача 5.3.3. Докажите справедливость результата, представленного на рисунке.
Рис.5.3.3. Демонстрация квантового параллелизма для функции с n -кубитовой областью определения.
Указание к задаче: воспользуйтесь результатами задачи
4.6.2.
133
Здесь обозначение  символизирует n - кубитовый провод (регистр запроса). Каждый кубит рассматриваемого провода подвергается преобразованию
символизирует n - кубитовый провод (регистр запроса). Каждый кубит рассматриваемого провода подвергается преобразованию
Адамара H , что обеспечивается тензорным произведением
H n . Область определения функции f (x) задана 2n
базисными состояниями |
x = 0 , 1 ,..., 2n −1 . |
Множество значений функции |
f (x) определяется всего |
двумя состояниями 0 и 1 . Квантовый параллелизм обеспечивает одновременное вычисление функции в 2n
точках от x = 0 до x = 2n −1.
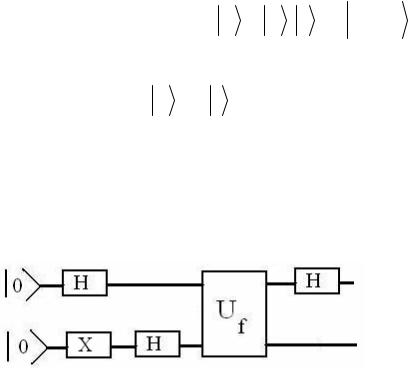
Алгоритм Дойча описывается квантовой схемой, приведенной на рисунке.
Рис.5.3.4. Квантовая схема для алгоритма Дойча
134
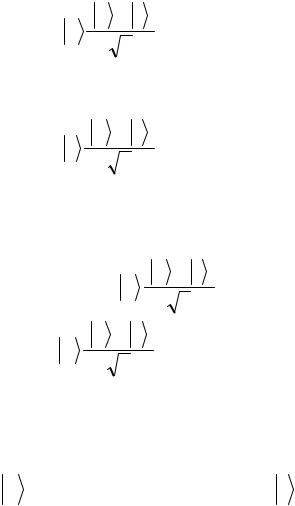
Задача 5.3.4. Покажите, что состояние на выходе схемы Дойча есть:
ψout = ± 0 |
(0 − 1 ) |
, |
(5) |
|
2 |
|
f (0)= f (1) |
когда функция постоянна, т.е. |
|||
ψout = ± 1 |
( 0 − 1 ) |
, |
(6) |
|
2 |
|
f (0) ≠ f (1) |
когда функция переменна, т.е. |
|||
Указание к задаче: |
покажите, что действие оператора Uf |
|
на состояние x |
( 0 − 1 ) |
приводит к состоянию |
|
2 |
|
(−1)f (x) x ( 0 − 1 ) |
|
|
2 |
|
|
Произведем измерение первого кубита выходного
состояния ψout , полученного в представленной выше задаче. В результате измерения с достоверностью получится
0 , если |
функция постоянна и |
1 , если функция |
переменна. |
Полученный результат |
весьма поучителен: |
135
посредством одногоединственного вычисления мы смогли идентифицировать определенное глобальное свойство функции (ее постоянство или переменность). При классическом рассмотрении задачи нам, очевидно, потребовалось бы два вычисления для решения той же самой задачи.
Заметим, что схема Дойча не ставит цели восстановить неизвестную функцию целиком: она ориентирована только на идентификацию рассматриваемого глобального свойства неизвестной функции.
Можно констатировать, что в алгоритме Дойча двухбитовая неопределенность, соответствующая четырем
возможным функциям f , снижается до однобитовой неопределенности, соответствующей только двум
возможным функциям f . Измерение на выходе схемы
Дойча позволяет отличить пару функций (1,2) от пары (3,4). Очевидно, что для того, чтобы отличить пару (1,3) от пары
(2,4), достаточно измерить f (0). Аналогично, что для того, чтобы отличить пару (1,4) от пары (2,3), достаточно
измерить f (1). Два последних алгоритма аналогичны в
классическом и квантовом случае. Возникает резонный вопрос: почему нет аналога алгоритму Дойча в классической теории информации? Дело в том, что в действительности нет двух раздельных теорий информации (классической и квантовой). Существует только одна последовательная теория информацииэто квантовая информатика. Классическая теория информацииесть «урезанная» версия квантовой (в классической теории бит
136

может находиться только в состояниях 0 или 1 , но не
их суперпозиции). Такое «урезание», как мы видим уже на примере алгоритма Дойча, делает теорию логически менее привлекательной, менее последовательной и фактически неполной. Напомним, что точно в таком же отношении друг к другу находятся классическая и квантовая теории вероятностей. Это неслучайно: ведь любое количественное определение информации (например, определение Шеннона) базируется на статистических соображениях.
Оказывается, что задача Дойча допускает простое обобщение на многокубитовый случай. Рассмотрим
функцию f (x) с n - битовой областью определения и 1-
битовым |
множеством значений. Теперь переменная x |
||
может |
принимать |
N различных |
значений |
x = 0,1,...,N −1, где N = 2n . Предположим, что нам |
|||
заранее известно, что функция |
f (x) может быть только |
||
одного из двух типов: постоянная функция или так
называемая сбалансированная функция. Для постоянной |
||
функции f (0) |
= f (1) =...= f (N −1). Если функция |
|
сбалансирована, |
то f (x)= 0 для некоторых |
x и |
f (x) =1 для остальных значений аргумента, причем |
||
значения f (x) |
= 0 и f (x) =1 встречаются одинаково |
|
часто (в этом и заключается сбалансированность). |
Пусть, |
|
137

например, имеется функция f (x) с 10-ти битовой областью определения. Тогда для некоторых 512 значений
x получим f (x)= 0, а для остальных 512 значений x
получим f (x) =1. Задача ДойчаДжозса состоит в том,
чтобы отличить постоянную функцию от сбалансированной. Алгоритм ДойчаДжозса является непосредственным обобщением алгоритма Дойча на случай многокубитовых систем. Он описывается следующей
квантовой схемой, приведенной на рисунке.
Рис. 5.3.5. Квантовая схема алгоритма ДойчаДжозса
Задача 5.3.5. Покажите, что на вход вычислителя
Uf |
в |
схеме ДойчаДжозса |
поступает состояние |
2n −1 |
|
(0 − 1 ). |
|
∑ x |
(7) |
||
x=0 |
2n |
2 |
|
138
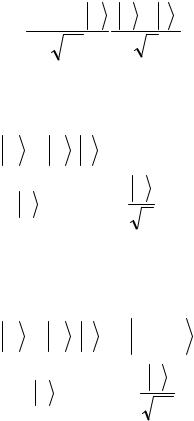
Uf |
Задача 5.3.6. Покажите, что на выходе вычислителя |
|||||||||||
в схеме |
ДойчаДжозса |
возникает |
состояние |
|||||||||
|
n |
|
|
f (x) |
x |
(0 − 1 ) |
|
|
(8) |
|||
∑(−1) |
|
|
|
|||||||||
2 |
|
−1 |
|
|
|
|
|
|
|
|
|
|
x=0 |
|
2n |
|
|
2 |
|
|
|
|
|||
|
|
|
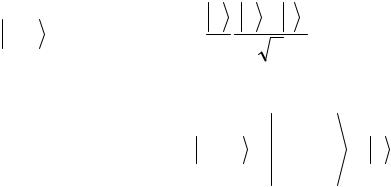
Задача 5.3.7. Убедитесь, что действие оператора |
|||||||||
Адамара |
|
|
H |
|
|
на |
базисные |
состояния |
||||
x = 0 , 1 отдельного кубита |
описывается |
формулой: |
||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
H x = ∑(−1)xz z |
|
. Покажите, что непосредственно из |
||||||||||
|
|
|
z=0 |
|
2 |
|
|
|
|
|
||
указанной формулы следует ее n - кубитовое обобщение: |
||||||||||||
действие оператора Уолша- |
Адамара H n на базисные |
|||||||||||
состояния |
|
n |
- |
|
|
кубитового |
регистра |
|||||
|
x = 0 , 1 ,..., 2n −1 |
описывается |
формулой: |
|||||||||
|
|
|
|
2n −1 |
|
z |
|
|
|
|
||
H n |
x = ∑(−1)xz |
. |
|
|
(9) |
|||||||
|
|
|
|
z=0 |
|
|
2n |
|
|
|
|
|
|
|
|
Здесь |
x = (x1,x2,...,xn ) |
и z = (z1, z2,...,zn )- |
|||||||
запись номеров состояний в двоичном представлении, x и z представляют собой n - компонентные строки из нолей
139
и единиц, xz = x1z1 + x2z2 +...+ xnzn - скалярное произведение соответствующих строк.
Непосредственно из результатов представленных
выше задач следует, что на выходе схемы УолшаАдамара возникает следующее n+1- кубитовое состояние:
2n −12n −1 |
xz+ f (x) z (0 − 1 ) |
|
||
ψout = ∑∑(−1) |
n |
2 |
(10) |
|
z=0 x=0 |
|
2 |
|
|
Проведем |
теперь |
измерение |
первых n кубитов |
|
(регистра запроса). Амплитуда вероятности найти регистр
запроса в состоянии |
z = 0 = 0,0,...,0 = 0 |
n |
||||
|
|
123 |
, |
|||
|
|
|
|
|
n |
|
очевидно, есть: |
|
|
f (x) |
|
|
|
|
2n−1 |
|
|
|||
M0,0,...,0 |
= ∑ |
(−1) |
. |
(11) |
||
n |
||||||
14243 |
x=0 2 |
|
|
|
|
|
n |
|
f (x) |
|
|
||
Пусть |
функция |
|
постоянна, т.е. |
|||
f (0)= f (1) =...= f (2n −1). В |
этом случае |
все |
||||
2n слагаемых в рассматриваемой сумме одинаковы (происходит их конструктивная интерференция), в итоге
суммарная амплитуда вероятности оказывается равной +1
140
