§ 31. Ленгмюровские колебания и волны в плазме. Плазмоны.

Рассмотрим теперь закон дисперсии высокочастотных продольных плазменных волн с частотой в области ленгмюровской частоты. Они известны как ленгмюровские волны и представляют собой важнейший тип возмущений, способных существовать и распространяться в плазме.

Закон дисперсии продольных волн определяет, как было показано выше, уравнение

,

в которое следует подставить продольную компоненту диэлектрической проницаемости. Если плазму считать холодной, то диэлектрическую проницаемость следует определять по формуле (4.19), и мы приходим к уравнению

Оно имеет два решения, отличающиеся знаком. Положительный корень равен

Как мы видим, в рассматриваемом случае частота волны совпадает с ленгмюровской частотой и не зависит от величины волнового числа. Фазовая скорость таких волн

уменьшается с увеличением волнового числа, а групповая скорость оказывается равной нулю:

Таким образом, в холодной плазме ленгмюровские волны не могут переносить энергию: фактически это обычные колебания плотности заряда, возникающие вследствие нарушения квазинейтральности плазмы. Если же мы учтем теперь тепловое движение частиц плазмы, то ситуация изменится кардинально. Диэлектрическую проницаемость определяет теперь формула (4.32) и дисперсионное уравнение для продольных волн становится таким:

или

Это уравнение несложно решить в общем виде. Но в интересующей нас сейчас высокочастотной области следует учесть, что ионы плазмы можно считать неподвижными, а потому их вклад в диэлектрическую проницаемость будет пренебрежимо малым. Формально это отвечает пределу , и уравнение (4.45) упрощается:

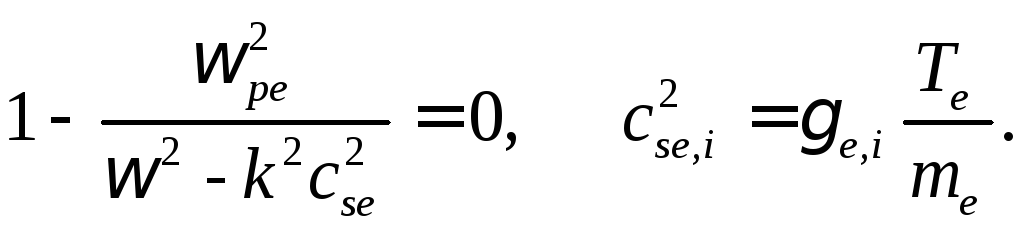
Теперь его уже не сложно решить, и мы, вновь выбирая положительный корень, получаем:

Это соотношение и определяет закон дисперсии ленгмюровской волны в плазме с конечной температурой.

Любопытно отметить, что это соотношение по виду оказывается вполне аналогичным известной формуле, определяющей связь энергии и импульса релятивистской частицы:

По этой причине о законе дисперсии (4.46) говорят как о «частице-подобном», а ленгмюровские волны в этом плане являются «квазичастицами», которые принято называть плазмонами.

Полезно отметить также, что закон дисперсии (4.46) можно записать в виде:

Второе слагаемое под корнем будет больше или порядка единицы, когда длина волны меньше дебаевского радиуса. В этом случае ленгмюровская волна сильно поглощается за счет механизма бесстолкновительного поглощения Ландау, так как оказывается резонансной по отношению к электронам плазмы,

По этой причине ленгмюровские волны могут существовать в плазме без существенного поглощения лишь в обратном пределе, когда их длина волны меньше дебаевского радиуса. В этом случае в (4.47) второе слагаемое под корнем можно считать малым и разложить по этой малости:

Аналогия с энергией частицы опять остается в силе, но теперь в нерелятивистском пределе, когда энергия связана с импульсом следующим образом:

В области частот ленгмюровских волн гидродинамическое описание, следствием которого фактически является закон (4.47), будет адекватным при выборе

Подставив это значение в (4.47), получим окончательно

И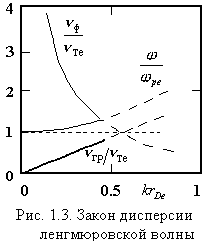менно об этом соотношении и говорят обычно как о законе дисперсии ленгмюровских волн в плазме. Строго говоря, он справедлив, как мы видели, лишь при выполнении сильного неравенства.Однако качественно закон дисперсии (4.48) остается в силе и при выполнении более мягкого условия, когда длина волны составляет несколько слагаемое в скобках в формуле (4.48) принято называть тепловой поправкой. Учет этой поправки приводит к тому, что групповая скорость ленгмюровской волны, в отличие от случая холодной плазмы, становится ненулевой (см. рис.1.3):

фазовая же скорость приближенно определяется формулой

При учете теплового движения частиц ленгмюровские волны получают возможность распространяться в плазме, перенося энергию.