§129 Флуктуации аддитивных величин. Рассмотрим величины, которые для всей системы связаны с аналогичными величинами подсистем по закону суперпозиции: ,

- номер подсистемы. - число подсистем.

Под , например, можно приближенно понимать энергию, когда подсистемы квазизамкнуты, то они стат. независимы.

Стат. независимость значит, что исистемы выражается произведением по соотв. Ф-циям подсистем:

(1)

Для таких ф-ций упрощается расчет средних значений случайных величин, которые описываются этими ф-циями.

Мы будем рассматривать флуктуации

Часто мерой флуктуации выступает дисперсия , или относительное среднеквадратичное отклонение (ОСКО)

Следствием вида ф-ций (1) имеем

и - разные подсистемы

это легко показать, если исп. вид ф-ций (1), где определение среднего по непрерыв. Фазовому пр-ву:

тогда с использованием (1):

вероятность отдельных подсистем

и если рассмотреть то

(a и b есть среди коэффициентов C,

т. е. a и b это подсистемы из множества всех подсистем K)

=учтем для=

=

  

=1

Можно писать

эта запись соответствует вообще то

такому виду записи,

а=

можно

писать

Теперь рассмотрим такое же среднее, по флуктуаций величин:

Учтем, что:

(1)

(2)дисперсия сл. вел.в подсистеме

тогда с учетом (1) и (2) : (3)

Посмотрим среднее от аддитивной наблюдаемой случайной величины:

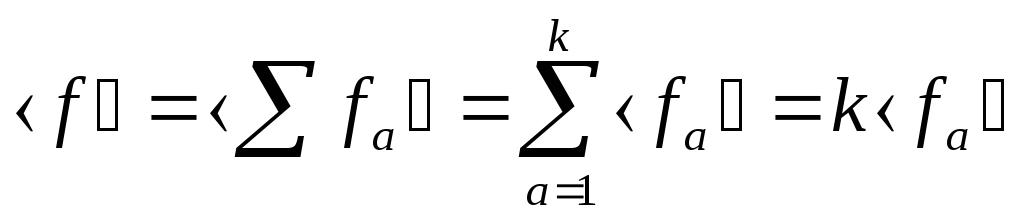
если разбиение системы на микроскопические системы таково, что они примерно равны, то говорят что тоже примерно равны для каждой подсистемы между собой, т. е. получили чтоне зависит от номера подсистемы.

K- число подсистем

Аналогично найдем дисперсию

т. к. -сумма, то и

т. е. дисперсия тоже обладает свойством

аддитивности и можно говорить что имеет

место такое соотношение

Найдем (это ОСКО):

(4)

Если система исходная достаточно величина, то число k можно сделать достаточно большим, поэтому пишут:

(из 4) , гдеN число частиц в системе.

Величина служит мерой вероятности отклонения величиныот ее среднего, или еслиучитывать эргодич. гипотезу, то это относительное время пребывания системы когда отлично от, где- параметр системы. Для достаточно больших систем, поэтому система почти все время пребывает в состоянии с параметром- с наиболее вероятным параметром.

§§ Энтропия и статистический вес.

Запишем определение энтропии:

Для канонического распределения мы установили это:

, где мы учли только один аддитивный интеграл движения E.

Тогда , по,а(*)

Соотношение (*) очень любопытное:

к этому привела аддитивность, и еще теорема Лиувилля.

тогда ,гдеэто вероятность состояния с энергией, т. е. это равновесное состояние.

Оценим

При рассмотрении кв. системы энергетические уровни образуют дискретное множество точек. Но для достаточно больших систем эти точки достаточно плотно расположены, и можно перейти к непрерывному распределению. Т. е. мы размазываем дискретный спектр по непрерывному. В этом нет ошибки, т. к. густота энергетических линий высока (линии очень близка друг к другу, т. е. переходит от к.)

Вводят . Запишем нормировку для.переходят в, гдеэто число состояний в интервале.



это плотность реализации состояния с

энергией , т. е. из интервала

А - это плотность состояния

Из малости имеем что система большую часть времени пребывает в состоянии с-энергией, ф вероятность пребывания в состоянииочень мала. Поэтому вид распределения:

E

Площадь под этой кривой можно рассчитать зная величину .

Мы знаем, что {, но это равно}

Параметруможно поставить в соответствии параметр:тогда, тогда

Взяв логарифмы, получим:

тогда (5)

Величина найденная таким образом называется статистическим весом.

Вероятность мультипликативная,-аддитивная.

Мы установили связь (5) энтропии и статистического веса, тогда -оценка статистического веса.

Энтропия определяется через статистическое усреднение. Это означает, что должны иметь достаточно большой по численности ансамбль систем, и провести усреднение. С другой сторон, если справедлива эргодич. гипотеза, то . Здесь стат. подход требует, чтобы время наблюдения было достаточно большим.

Энтропия это статистич. параметр, и все параметры, определяемые через энтропию, тоже статистические, т. е. они должны опр. на системах с большим числом частиц, с большим числом степеней свободы.