§ 6 Роль классической механики в квантовой механике

Два момента присутствия классической механики в квантовой механике

1. Измерение микросистем (квантово-механических систем) проводятся с помощью классических приборов (систем)

2. Принцип соответствия – переход квантово-механических результатов в классическую механику (  0. Можно ввести такую величину размерности действия A, что ).

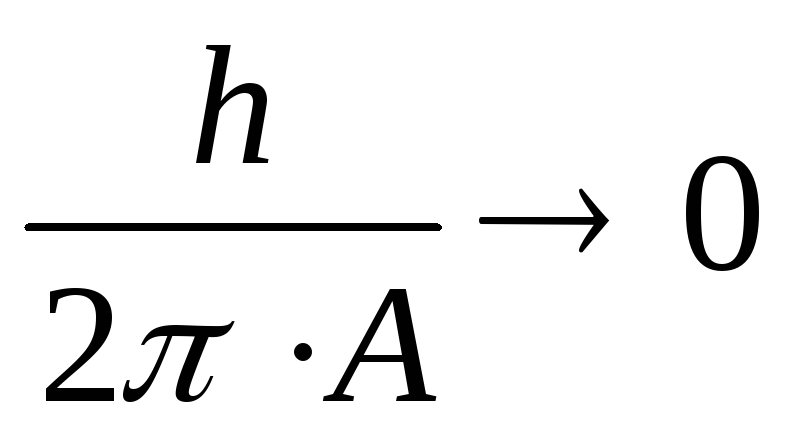По Эйнштейну этот переход характеризуется . Если, то переход в классическую механику Ньютона.

§ 7 Волновая функция и ее свойства.

Волновая функция динамических переменных и времени определяет состояние системы точностью до фазового множителя. Т. е.

т. е. ,описывает одно и тоже состояние, где- фазовый множитель.

Волновая функция – комплексная, непрерывная, конечная. У нее почти всюду существует конечная производная по координате, но в некоторых точках может терпеть скачек (особые точки).

Функции - нормируемые, т.е. квадратично интегрируемы. Но для свободной материальной точкине нормируема.

- элементарный объем

- вероятность того, что динамические переменные лежат в интервале.

Это определение справедливо для квадратично интегрируемых функций.

Для не квадратично интегрируемых функций величина пропорциональна плотности вероятности.

§ 8 Принцип суперпозиции состояний

Если мы имеем состояние системы, описываемое функцией , то суперпозиции этих функций отвечает некоторое состояние этой системы

Иначе: если - состояние некоторой системы, то суперпозиция этих состояний также является состоянием этой системы.

Отсюда получаем: уравнения, которым подчиняется - функция должны быть линейными.

Этот же вывод распространяется и на операторы и на операторы в квантовой механике. Принцип суперпозиции требует использования в квантовой механике линейных операторов.

§ 9 Понятие о теории представлений

Представление – это совокупность переменных в которых решается задача (т. е. набор динамических переменных).

Рассмотрим одну материальную точку. Число степеней свободы n=3.

Здесь могут быть 2 случая:

1. Под понимаем имеем-представление (координатное)

2. Под понимаем имеем-представление (импульсное)

Операторы в -представлении:

Оператор координаты

Оператор импульса 

Здесь

Операторы в -представлении

Оператор координаты 

Оператор импульса

Здесь

Мы в основном будем использовать -представление.

Результаты измерения от вида представления не зависят!

§ 10 Операторы в квантовой механике

В силу принципа суперпозиции в квантовой механике используются линейные операторы.

Линейный оператор – это такой оператор действующий на, что

(1)

(2)

здесь

1. – задача Штурма-Лиувилля

2. - действует на произвольную функцию.

Линейность:

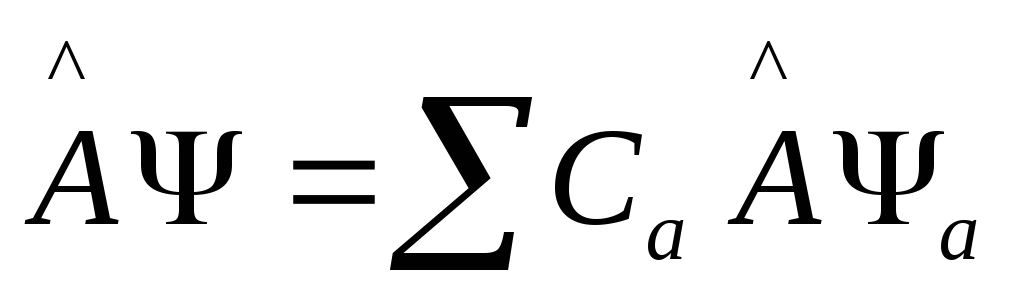Если , то(3)

т.к. , то из (3)

Сопряженный оператор – это оператор, который связан с данным оператором соотношением:

или

Отсюда

Если - то оператор называется эрмитовым.

Транспонированный оператор

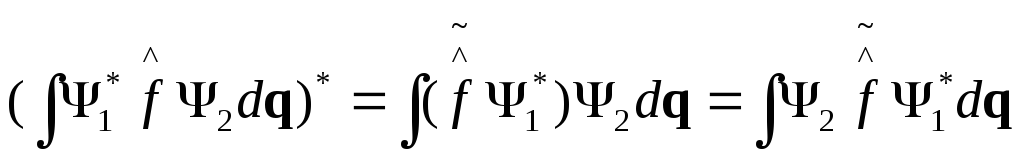
Отметим следующие свойства:

1)

(4)

Из выражения (4) получаем

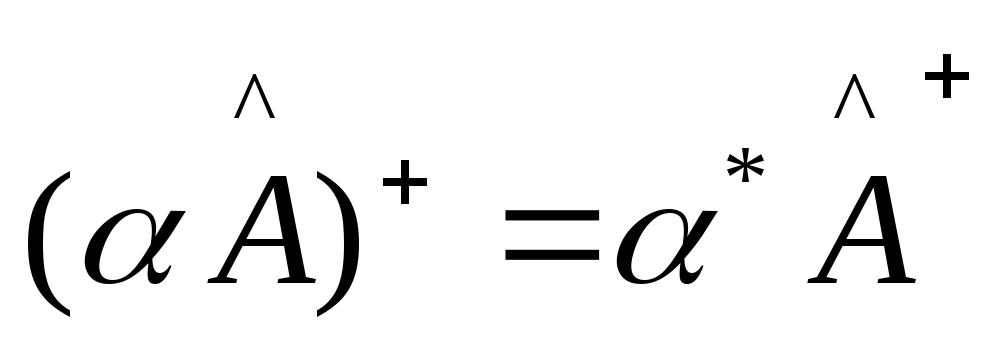
2)

3)

Сумма операторов: . Это операторное равенство предполагает

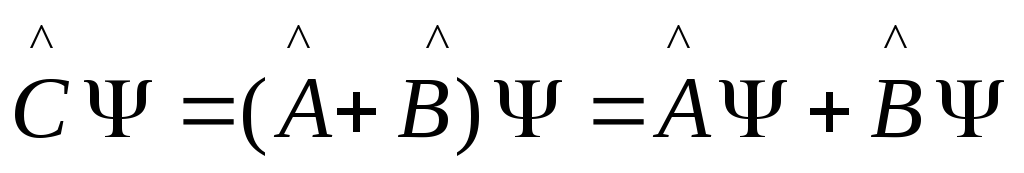
Произведение операторов: , тогда 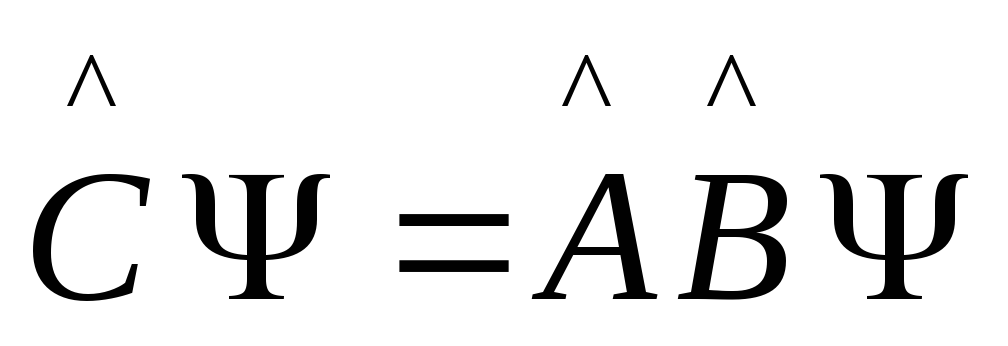. Это операторное равенство предполагает

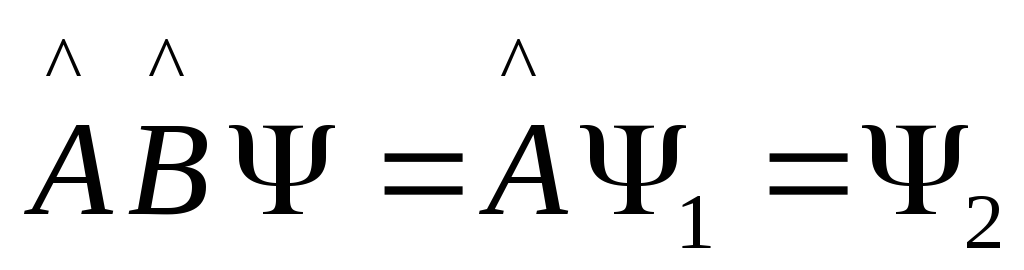
В общем случае не коммутативны

Коммутатор

Если , то операторы коммутативны.

Если , то операторы не коммутативны.

Так как физические величины вещественны, то число операторов в квантовой механике сужается.

Сужение класса операторов – эрмитовость операторов.

Запишем определение среднего:

Так как результаты измерений вещественны, то тоже должно быть вещественным, т.е.

(5)

тогда

,

т.е.

Обозначим , тогда

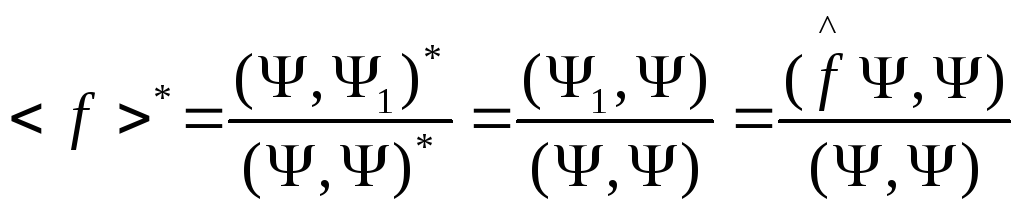
Тогда из (5) получаем

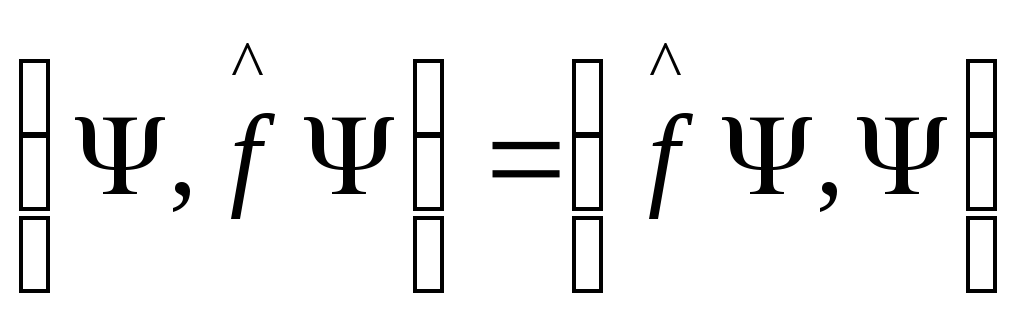(6)

Из (6) имеем для любых :

,

,

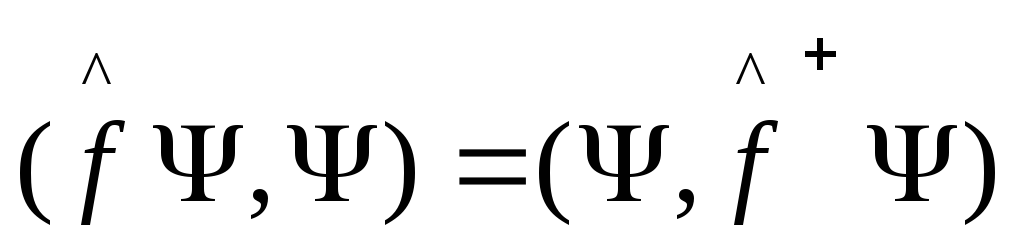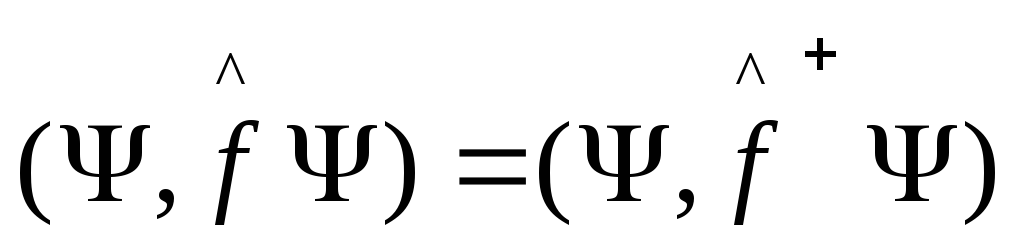где (сопряженный и транспонированный)

§ 11. Собственные функции и собственные значения эрмитовых операторов. Случаи дискретного и непрерывного спектров.

Начнем с дискретного спектра, т.к. ему соответствует квадратичноинтегрируемые функции.

Задача Штурма-Лиувилля дискретного спектра

(1)

-собственные функции

- собственные значения

Так как эрмитов, то его собственные значения вещественны.

Расчет среднего . Если речь идет о физической величине, тоэто волновые функции (описывающие состояние системы). Если речь идет о математическом аппарате, то- это любые функции.

Как частные случай рассмотрим , где- собственные функции оператора. Тогда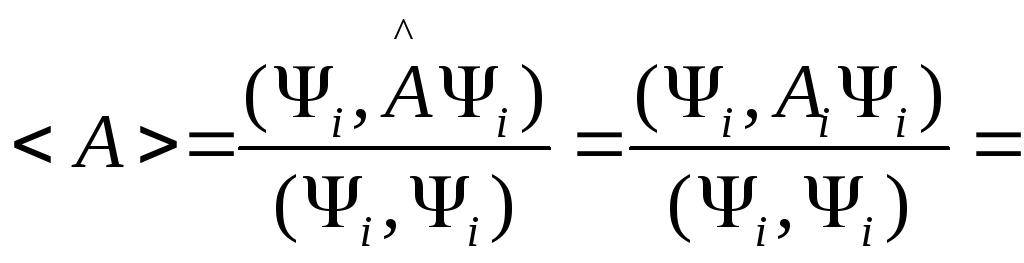{Так как- число, то его можно вынести за знак скалярного произведения}- это среднее значение величинывi-ом квантовом состоянии.

Так как среднее – вещественно, то и собственные значения вещественны.

Для эрмитова оператора собственные значения вещественны. Все эрмитовы операторы имеют вещественные спектры.

Рассмотрим теперь

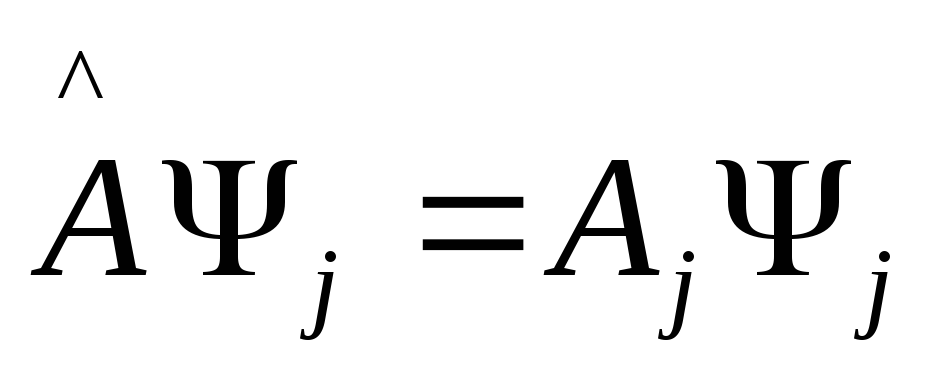
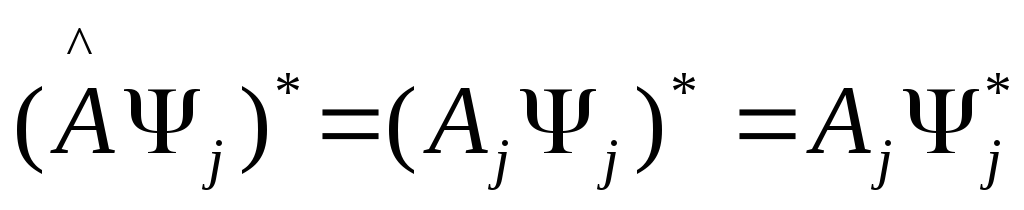(2)

Умножая (1) скалярно на слева, получим

(3)

Теперь (2) умножаем справа на , тогда

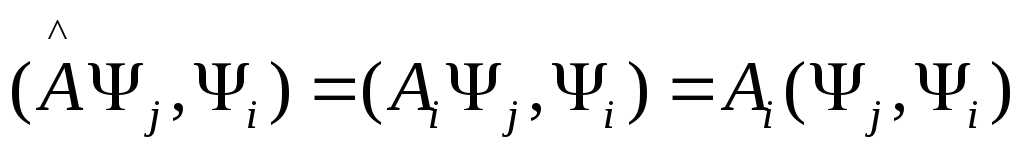(4)

Почленно из (3) – (4):

(5)

т.к. - эрмитов, то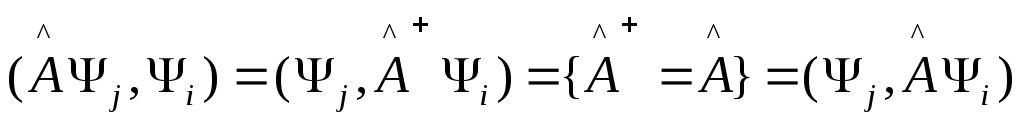. Из (5) имеем

. (6)

Рассмотрим случай невырожденного спектра:

Спектр вырожденный, если одному собственному значению

соответствуют несколько собственных функций.

Например:

Невырожденный спектр – все собственные значения различные.

1) Рассмотрим (6) при , тогда,.

2) Теперь пусть . В этом случае скалярное произведение. Обычно вводят нормировку.

1 и 2 дает условие ортонормируемости .

Утверждается, что собственные функции эрмитового оператора с дискретным спектром образуют полную систему, т.е. обладают свойством полноты. Это верно для функций квантовой механики. Утверждение означает, что произвольную функцию можно разложить по собственным функция эрмитовова оператора как по базису.

Запишем это разложение:

, (9)

где индекс i пробегает по всем значениям, удовлетворяющим задаче (1).

Формулу (9) следует отличать от принципа суперпозиции

,

где - вес состоянияи суммирование ведется по произвольнымa=1,…,k. Заметим, что если (модель Юнга с ширмой и электроном), то.

Найдем коэффициенты из (9). Домножим скалярно (9) на, тогда имеем{из условия ортонормированности}=

,

тогда из (9) получаем

, (9^/)

Далее

Из (9^/) также можно получить еще одно соотношение:

- равенство Парсеваля (условие замкнутости).

Теперь рассмотрим случай непрерывного спектра.

- у собственной функции индексом является собственное значение. Собственные значения непрерывны, они сплошь заполняют соответствующую числовую ось.

В этом случае собственные функции не нормируемы (квадратично не интегрируемы).

Используем искусственную операцию – введем понятие собственных дифференциалов, по определению:

,

т. е. на числовой оси рассмотрим функции с равным весом на интервале .

Собственные дифференциалы (12) квадратичноинтегрируемы. Через рассмотренные собственные дифференциалы приходим к рассмотрению собственных функций.

Условие ортонормируемости: .

Здесь уже дает расходящийся интеграл, т. е. равен.

Собственные функции обладают свойством полноты, т. е. они образуют базис по которому может быть разложена любая функция:

, (13)

По аналогии с дискретным спектром:

- равенство Парсеваля