
- •Квантовая механика
- •§ 1. Экспериментальные основы квантовой механики
- •§ 2. Классическое и квантовое описание системы.
- •§ 3 Принцип неопределенности.
- •§ 4. Полный набор динамических переменных
- •§ 5. Постулаты квантовой механики.
- •§ 6 Роль классической механики в квантовой механике
- •§ 7 Волновая функция и ее свойства.
- •§ 8 Принцип суперпозиции состояний
- •§ 9 Понятие о теории представлений
- •§ 10 Операторы в квантовой механике
- •§ 12 Среднее значение измеряемой величины.
- •§ 13 Вероятность результатов измерения
- •§ 14 Коммутативность операторов и одновременная измеримость физических величин
- •§ 15. Операторы координаты , импульса, момента импульса, энергии.
- •§ 16. Решение задачи Штурма-Лиувилля для оператора .
- •§ 17 Решение задачи Штурма-Лиувилля для оператора .
- •§ 18. Вычисление коммутаторов, содержащих операторы .
- •§ 19 Волновое уравнение
- •§ 20 Производная оператора по времени
- •§ 21 Интегралы движения в кв. Механике.
- •§ 22. Свойства операторов вида
- •§23. Флуктуации физических величин.
- •§ 24. Неравенство Гайзенберга.
- •§ 25 Оператор Гамильтона различных систем.
- •§ 26. Стационарное состояние различных систем
- •§ 27. Решение волнового уравнения в случае свободной материальной точки
- •Для трехмерного случая
- •§ 28. Интегральные операторы в квантовой механике.
- •§ 29. Интегральный оператор канонического преобразования.
- •§ 30. Каноническое преобразование оператора.
- •§ 31. Уравнения Шредингера в матричной форме.
- •§ 32. Линейный гармонический осциллятор
- •Предельные технологические размеры кристаллов и.С. 0.1 – 0.5 мкм. Существует и предел по физической работоспособности. Однако с уменьшением размера кристалла увеличивается быстродействие приборов.
- •§ 30.1. Каноническое преобразование оператора. Ч. 2
- •§ 34. Унитарные инварианты в квантовой механике.
- •§ 35. Вид операторов ив декартовых и сферических координатах.
- •§ 36. Коммутационные соотношения с оператором .
- •§ 37. Собственные функции и собственные значения операторов и.
- •§ 38. Вырождение энергетических уровней частицы, движущейся в центральном поле.
- •§ 39. Гамильтониан частицы без спина, движущейся в магнитном поле.
- •§ 40. Снятие вырождения по квантовому числу m в случае частицы без спина, движущейся в магнитном поле. Используем
- •§ 41. Оператор бесконечно малого поворота без учета спина.
- •§ 42. Собственный механический момент (спин).
- •§ 43. Операторы ии их свойства.
- •§ 44. Спиновая переменная волновой функции
- •§ 45. Матрицы Паули и их свойства.
- •§ 46 Понятие о спинорах
- •§ 47. Уравнение Паули Мы писали волновое уравнение в виде
- •§ 48. Операторы и, и их свойства
- •§ 50. Принцип тождественности.
- •§ 51. Оператор перестановки и его свойства
- •§ 52. Симметричное и антисимметричное состояния.
- •§ 53. Обменное взаимодействие
- •§ 54. Основное состояние атома гелия
- •§ 55. Схема Юнга квантовой механики.
- •1. И ,
- •2. И .
- •§ 56. Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: нулевое и первое приближения.
- •§ 58 Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: второе приближения.
- •§ 59. Критерий применимости теории возмущений.
- •§ 60. Стационарная теория возмущений в случае близких энергетических уровней.
- •§ 61. Метод (представление) Шредингера. Оператор эволюции и его свойства.
- •§ 62. Метод (представление) Гейзенберга. Уравнение движения для оператора.
- •§ 63. Уравнение эволюции среднего значения физической величины. Соотношение неопределенности: время – энергия.
- •§ 64. Матричное представление операторов.
- •§ 65. E – представление.
- •§ 66. Уравнение Шредингера в матричной форме.
- •§ 67. Матричная формулировка задачи о линейном гармоническом осцилляторе.
- •§ 68. Расчет матричных элементов операторов .
§ 58 Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: второе приближения.
При n=2 возможно:
p=2, q=0; p=1, q=1; p=0,q=2.
Для членов второго порядка малости запишем из (3)
![]() (9*)
(9*)
Теперь запишем для 2-го порядка выражение (5*):
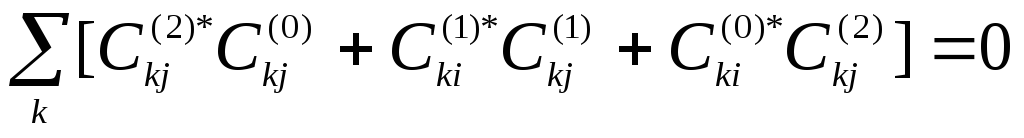 (10*)
(10*)
Рассмотрим
случай
![]() :
:
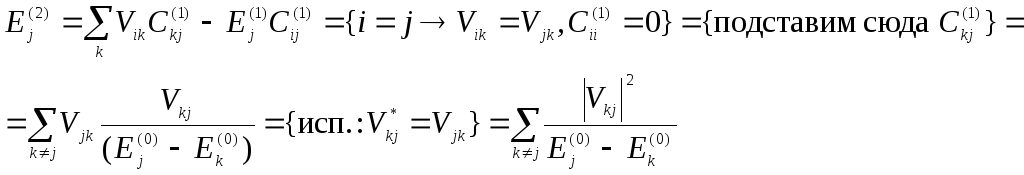 Получили
поправку второго порядка малоси к
энергетическому уровню основного
состояния. Пусть j-
основное состояние
Получили
поправку второго порядка малоси к
энергетическому уровню основного
состояния. Пусть j-
основное состояние
![]() (так как спектр невырожденный). Тогда
знаменатель в поправке второго порядка
всегда отрицательный. Тогда поправка
всегда отрицательна.
(так как спектр невырожденный). Тогда
знаменатель в поправке второго порядка
всегда отрицательный. Тогда поправка
всегда отрицательна.
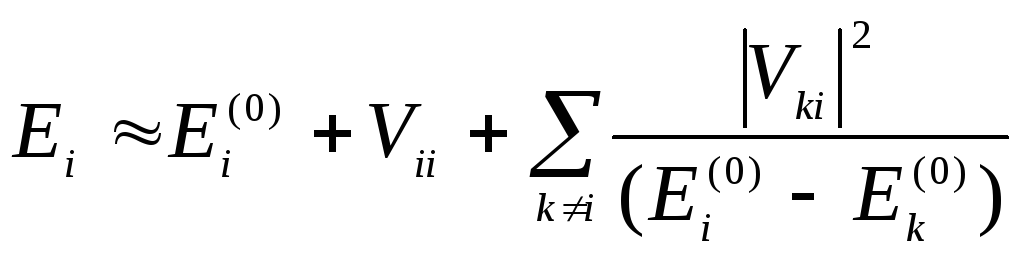 .
.
Рассмотрим
теперь (10*): его можно в общем случае
записать, учмтывая, что
![]() :
:
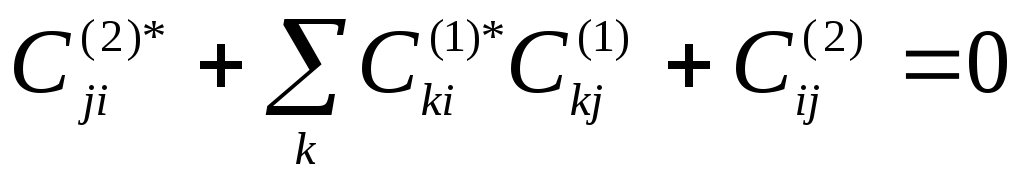
Рассмотрим
случай
![]() :
:
![]()
Из
этого цравнения находим дейтсвительную
часть
![]() ,
а мнимая часть обращается принудительно
в ноль.
,
а мнимая часть обращается принудительно
в ноль.
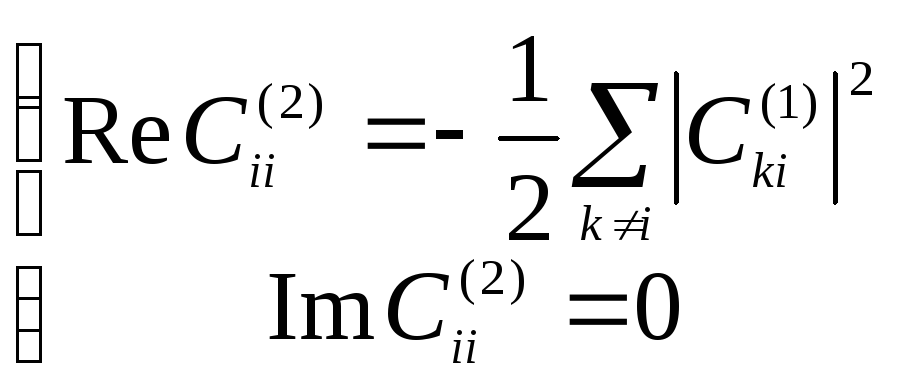 (11*)
(11*)
Случай
![]()
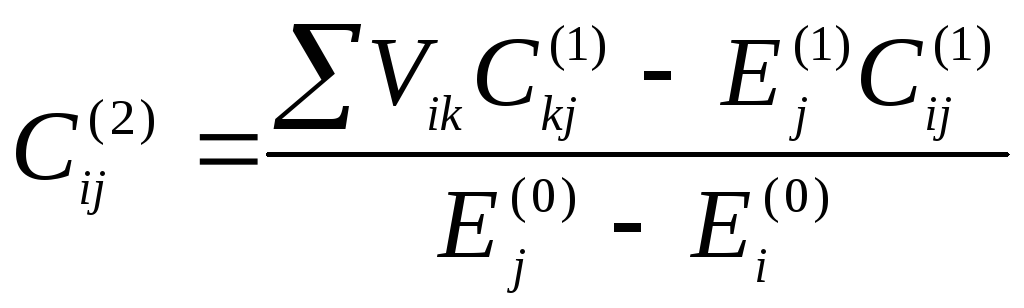 .
.
Обычно пишут
 Тогда
Тогда
![]() .
.
§ 59. Критерий применимости теории возмущений.
Имеем волновые функции:
-
не возмущенное состояние
![]() .
.
-
возмущенные состояния
![]() ,
где
,
где![]() .
.
Обе они нормированы на единицу:
![]()
![]()
Теория возмущений работает, если поправка к невозмущенной функции мала.
![]()
Ранее получено
![]()
Кроме того
![]() ,
,
где p – порядок малости в теории возмущений.
Теория срабатывает если поправка мала по сравнению с нормой функции, тогда критерий применимости теории возмущений
![]() (4)
(4)
Также можно использовать другие соотношения, например
![]()
Рассмотрим критерий малости (4)
![]() .
.
Штрих
над суммой означает, что при суммировании
выбрасывем значения с
![]() ,
т. е. суммирование по
,
т. е. суммирование по![]() ,
где
,
где![]() .
.
Раньше
получали
![]() для
для![]() ,
тогда
,
тогда
![]()
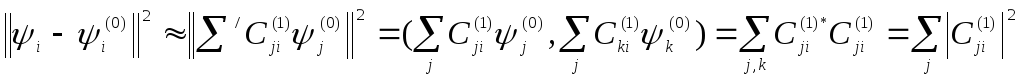 Тогда
при
Тогда
при
![]() получаем критерий применимости теории
возмущений в виде неравенства
получаем критерий применимости теории
возмущений в виде неравенства
![]() ,
,
но этот критерий не всегда верен. Однако если он не выполняется, то теория возмущений точно не выполняется.
Этот критерий дает условие:
![]() . (5)
. (5)
Отсюда ясно, что если имеются вырожденные уровни, то требуется модификация метода.
Будем
считать под
![]() состояние системы:
состояние системы:![]() .
.
![]() ,
,
то
![]() ,
,
тогда
![]() .
.
§ 60. Стационарная теория возмущений в случае близких энергетических уровней.
Пусть у нас два близких уровня, а остальные уровни хорошо удовлетворяют критерию (5)
Пусть
близкие уровни – это уровни
![]() .
Близость уровней определяется из
критерия (5).
.
Близость уровней определяется из
критерия (5).
Модификация
теории возмущений состоит в том, чтобы
в качестве нулевого приближения для 1
и 2 состояния подобрать такие функции
![]() и
и![]() ,
которые обращали бы в ноль
,
которые обращали бы в ноль![]() - числитель критерия (5).
- числитель критерия (5).
По определению:
![]() .
.
Мы рассмотрим набор
 .
.
Очевидно, что
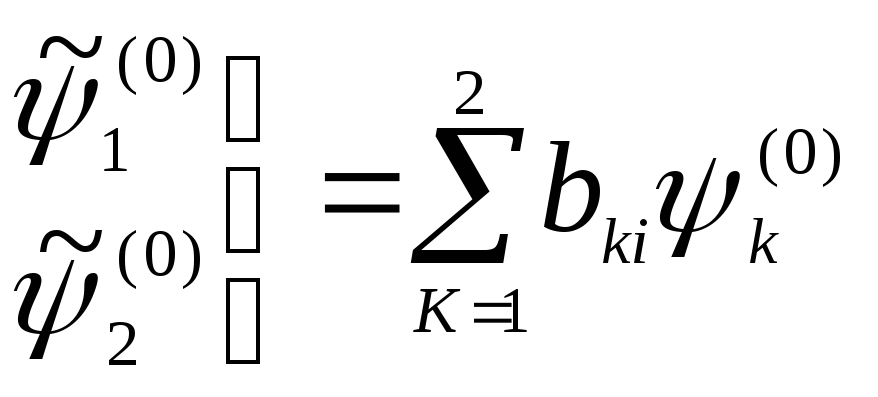 .
.
Распишем:
![]()
![]()
Рассмотрим свойства невозмущенной функции:
Они удовлетворяют ЗШЛ:
![]() ,
,
где
![]() - невозмущенный оператор.
- невозмущенный оператор.
![]() (6)
(6)
Эта матрица имеет диагональный вид, т. к. мы рассматриваем матричные элементы на собственных функциях этого оператора.
Мы
ввели
![]() и
и![]() для итого, чтобы ввести такой матричный
элемент, чтобы он
для итого, чтобы ввести такой матричный
элемент, чтобы он
![]() ,
,
тогда
(5) будет для
![]() и
и![]() давать 0 и теория возмущений будет
работать.
давать 0 и теория возмущений будет
работать.
Таким
образом мы ввели новый невозмущенный
базис
![]() и
и![]() .
В этом новом базисе мы должны диаганализовать
.
В этом новом базисе мы должны диаганализовать![]() ,
,![]()
Искомое
преобразование является унитарным, так
как оно не нарушает условия нормировки.
Надо подобрать коэффициенты
![]() :
:
![]() .
.
Используем
![]()
![]()
Но
![]() ,
,
или в матричном виде
![]()
![]()
![]()
Из
свойства ортонормированности найдем
свойства коэффициентов
![]()
![]() ,
,
т.е.
![]()
Это унитарное преобразование, оно сохраняет нормировку.
Запишем ЗШЛ для модифицированных функций.
![]() ,
,
![]() ,
,
тогда
подставим явно
![]() и
и![]()
![]() ,
,
![]() .
.
Рассмотрим
случай i=1,
умножим левую и правую части этого
уравнения скалярно на
![]() и
и![]() ,
тогда имеем:
,
тогда имеем:
![]() ,
,
![]() .
.
Введем обозначения:
![]() .
.
Тогда имеем
![]() ,
,
![]() .
.
Перепишем эти уравнения в виде
![]() , (7)
, (7)
![]() .
.
Система
линейных однородных уравнений. Она
имеет нетривиальное решение только при
![]() .
.
Обозначим
![]() ,
,
![]()
 .
.
Имеем решение
![]() .
.
При i=2, то по аналогии
![]() ,
,
![]()
и обозанчив
![]()
получаем
![]() ,
,
![]() .
.
Во втором случае решение аналогично первому. Однако мы приписываем одному знак +, а другому -.
Имеем тогда уровни энергии:
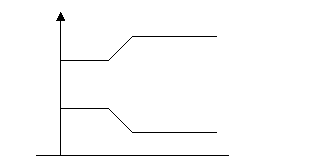
Перейдем к системе (7). Из нее имеем
![]() ,
,
![]() .
.
Кроме этого используем соотношение
![]() ,
,
т.е. имеем нормировку
![]() .
.
Рассмотрим
![]() (и аналогично
(и аналогично![]() )
)
![]() ,
,
![]() .
.
Введем обозначение:
![]() ,
,
где
![]() и
и![]() - вспомогательные углы, определяемые
через матричные элементы
- вспомогательные углы, определяемые
через матричные элементы![]() ,
,![]() и
и![]() .
.
Тогда
коэффициенты
![]() имеем в виде
имеем в виде
![]() ;
;
![]() ,
,
![]() ;
;
![]() .
.
Таким
образом при
![]() теория возмущений срабатывает для двух
близких уровней. Теперь в качестве
нулевого приближения берут:
теория возмущений срабатывает для двух
близких уровней. Теперь в качестве
нулевого приближения берут:

Модификация касалась только этих двух близких состояний. Остальные состояния не модифицировались, т. к. они сразу удовлетворяли критерию.
Теперь
![]() и
и![]() - теория возмущений работает.
- теория возмущений работает.
