
Методичка по электричеству / Электричество лекции / 15
.RTF
Применим
теперь операцию
 к (7.11):
к (7.11):
 .
.
Тогда
 .
Учтем
уравнение
непрерывности:
.
Учтем
уравнение
непрерывности:

и
получим:
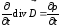 и
и
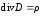 ,
что
совпадает с продифференцированным по
времени уравнением
(7.14).
,
что
совпадает с продифференцированным по
времени уравнением
(7.14).
Это
означает, что система уравнений Максвелла
не переполнена.
В
ней содержится 8 скалярных уравнений и
6 неизвестных компонент векторов
 и
и
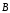 .
.
Физический смысл уравнений Максвелла:
-
(7.11). Источником магнитного поля
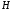 являются ток проводимости и переменное
электрическое поле.
являются ток проводимости и переменное
электрическое поле.
-
(7.12). Источником электрического поля
 являются
неподвижные электрические заряды (при
этом поле потенциально) и переменное
магнитное поле
(при
этом электрическое поле
является
вихревым).
являются
неподвижные электрические заряды (при
этом поле потенциально) и переменное
магнитное поле
(при
этом электрическое поле
является
вихревым).
-
(7.13). Не существует магнитных зарядов; силовые линии магнитного поля являются замкнутыми; поле является вихревым.
-
(7.14). Потенциальное электрическое поле имеет источником неподвижные заряды, силовые линии вектора электрического смещения начинаются на
 и заканчиваются на
зарядах
и заканчиваются на
зарядах
 .
.
Уравнения Максвелла и материальные уравнения дополняются формулой для плотности энергии электромагнитного поля:
 . (7.16)
. (7.16)
§ 7.3. Закон сохранения энергии электромагнитного поля.
Поток энергии.
Уравнения Максвелла необходимо дополнить соотношениями, выражающими закон сохранения энергии.
При изменении электромагнитного поля в среде и прохождении через нее электрического тока в единице объема среды совершается элементарная внешняя работа:
 .
.
Формула
получена из (7.16) с учетом закона
Джоуля-Ленца (5.9).
Если
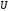 - внутренняя энергия единицы объема
среды, то:
- внутренняя энергия единицы объема
среды, то:
 ;
;
 . (7.17)
. (7.17)
Первые два слагаемых – электромагнитная часть плотности энергии, третье - тепловая часть (джоулево тепло). Преобразуем (7.17) к виду:
 . (7.18)
. (7.18)
Используя (7.11) и (7.12), имеем с учетом формул (7) Приложения:
 , (7.19)
, (7.19)
где
 - оператор набла (1.18). Введем обозначение:
- оператор набла (1.18). Введем обозначение:
 . (7.20)
. (7.20)
Тогда:
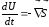 или
или  (7.21)
(7.21)
В интегральной форме уравнение (7.21) имеет вид:
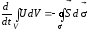 . (7.22)
. (7.22)
Вектор
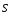 называется
вектором Умова-Пойнтинга (1874 г.,
1884 г.).
называется
вектором Умова-Пойнтинга (1874 г.,
1884 г.).
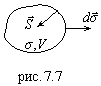
 -
это поток вектора
-
это поток вектора
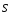 сквозь замкнутую поверхность
сквозь замкнутую поверхность
 .
Знак “‑“ показывает, что
.
Знак “‑“ показывает, что
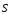 и
и
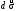 разнонаправлены, если поток положителен.
разнонаправлены, если поток положителен.
 - это электромагнитная энергия объема,
заключенного внутри замкнутой поверхности
- это электромагнитная энергия объема,
заключенного внутри замкнутой поверхности
 (см.рис.7.7).
(см.рис.7.7).
Тогда, вектор Умова-Пойнтинга определяет энергию электромагнитного поля, пересекающую в единицу времени площадку единичной площади, перпендикулярную направлению распространения этой энергии.
Размерность
вектора
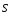 - Вт/м2.
- Вт/м2.
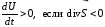 ,
т.е. энергия в объеме увеличивается за
счет потока вектора
,
т.е. энергия в объеме увеличивается за
счет потока вектора
 внутрь
поверхности.
внутрь
поверхности.
§ 7.4. Поток энергии в линиях электропередачи.
Применим полученные выше результаты для энергии электромагнитного поля к процессам передачи энергии.
Основной
вывод, который можно сделать из (7.20), это
то, что энергией обладают не заряды на
проводниках, а электрическое и магнитное
поле, распределенное в пространстве.
Мощность передаваемой энергии определяется
не непосредственно током или напряжением,
а потоком вектора
 .
.
Рассмотрим это вначале на примере стационарных полей.
Пусть
два провода проходят в направлении,
перпендикулярном плоскости рис.7.8. В
одном проводе ток идет к потребителю,
а в другом – обратно к источнику.
Напряженность электрического поля
между проводами: 
 ,
,
где
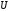 - разность потенциалов. Напряженность
магнитного поля найдем по теореме о
циркуляции:
- разность потенциалов. Напряженность
магнитного поля найдем по теореме о
циркуляции:
 ;
; 
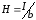 ,
,
где
 и
и
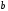 - размеры, показанные на рис.7.8. Вектор
- размеры, показанные на рис.7.8. Вектор
 параллелен оси поводов и направлен к
потребителю. Поток
параллелен оси поводов и направлен к
потребителю. Поток
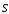 по всему сечению
по всему сечению
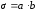 равен:
равен:
 ,
,
т.е. совпадает с передаваемой мощностью.
Одинаковый
результат достигнут при различных
физических картинах. В случае
 передача энергии идет по проводам. В
случае
передача энергии идет по проводам. В
случае
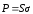 энергия идет вне провода, причем плотность
потока энергии в любой точке пространства
определяется вектором
энергия идет вне провода, причем плотность
потока энергии в любой точке пространства
определяется вектором
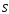 .
.
В
предыдущем рассмотрении мы считали
проводники идеальными, поэтому
электрическое поле внутри проводника
отсутствует:
 .
Если учесть проводимость проводника,
то:
.
Если учесть проводимость проводника,
то:
 .
.
Видно,
что появилась составляющая 
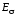 ,
направленная так же, как ток
,
направленная так же, как ток
 .
В силу теоремы о циркуляции:
.
В силу теоремы о циркуляции:
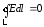
 ,
,
т.е.
точно такое же поле существует вне
проводника. Тогда появляется вектор
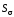 ,
направленный по радиусу к оси проводника
(рис.7.9).
,
направленный по радиусу к оси проводника
(рис.7.9).
Найдем
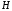 по теореме о циркуляции для проводника
круглого сечения:
по теореме о циркуляции для проводника
круглого сечения:
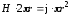 ;
; 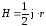 .
.
Тогда:
 .
.
Через
боковую поверхность на длине
 втекает мощность:
втекает мощность:
 ,
,
где
 - сопротивление проводника.
- сопротивление проводника.
Джоулево
тепло
(5.10),
выделяемое на длине
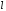 проводника в 1 секунду:
проводника в 1 секунду:
 .
.
Таким
образом,
 ,
т.е. при прохождении постоянного
электрического тока через проводник с
удельным сопротивлением
,
т.е. при прохождении постоянного
электрического тока через проводник с
удельным сопротивлением
 выделяемая
в виде теплоты энергия поступает через
боковую поверхность из окружающего
пространства, где движется энергия
электрического и магнитного полей.
выделяемая
в виде теплоты энергия поступает через
боковую поверхность из окружающего
пространства, где движется энергия
электрического и магнитного полей.
Введем следующие обозначения:
 -
это поток энергии, передаваемой
потребителю;
-
это поток энергии, передаваемой
потребителю;
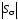 - потери на джоулево тепло в подводящих
проводах. Суммарный вектор (рис.7.10, а):
- потери на джоулево тепло в подводящих
проводах. Суммарный вектор (рис.7.10, а):
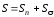
должен
быть перпендикулярен силовым линиям
электрического поля. Ясно, что реальная
картина силовых линий отлична от
приведенной ранее на рис.7.8 и выглядит,
как на рис.7.10, б. В точке А
векторы напряженности электрического
поля направлены так, как на рис.7.10, в,
где вектор 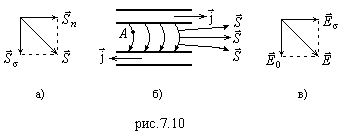
 характеризует
поле в отсутствие потерь на сопротивление
проводов. Из рис.7.10, б видно, что потери
приводят к отклонению
характеризует
поле в отсутствие потерь на сопротивление
проводов. Из рис.7.10, б видно, что потери
приводят к отклонению
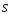 от направления вдоль длины провода.
от направления вдоль длины провода.
Понятно,
что в случае переменного
тока малой (промышленной) частоты картина
качественно не изменится. Мощность
передаваемой энергии определяется
потоком
 и распространяется вне провода вдоль
него. В случае двухпроводной линии
используемая потребителем (полезная)
мощность движется параллельно проводам
в пространстве между ними. Потери на
джоулево тепло в проводах определяются
поступающей через боковую поверхность
провода энергией.
и распространяется вне провода вдоль
него. В случае двухпроводной линии
используемая потребителем (полезная)
мощность движется параллельно проводам
в пространстве между ними. Потери на
джоулево тепло в проводах определяются
поступающей через боковую поверхность
провода энергией.
Отличие
от постоянного тока в том, что при
определении
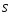 нужно учесть разность фаз
нужно учесть разность фаз
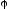 между током и напряжением. При
между током и напряжением. При

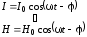 .
.
Тогда:
 .
Среднее по времени:
.
Среднее по времени:
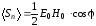 .
Подставляя вместо
.
Подставляя вместо
 их значения
их значения
 ,
получим поток
,
получим поток
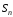 через сечение
через сечение
 ,
т.е.:
,
т.е.:
 , (7.23)
, (7.23)
что совпадает с формулой для мощности переменного тока.
§ 7.5. Электромагнитные волны в вакууме.
а) Волновое уравнение.
Запишем
уравнения Максвелла (7.11-7.15) для вакуума
при
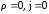 :
:
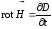 ; (7.24)
; (7.24)  ; (7.26)
; (7.26)
 ; (7.25)
; (7.25)  . (7.27)
. (7.27)
Материальные уравнения:
 . (7.28)
. (7.28)
Учтем, что:
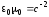 . (7.29)
. (7.29)
Оставим
в уравнениях (7.24-7.27)
лишь векторы
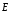 и
и
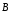 :
:
 ;
; 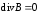 ;
;
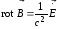 ;
;  .
.
Введя
оператор “набла”
 ,
запишем последние четыре уравнения в
виде:
,
запишем последние четыре уравнения в
виде:
 ; (7.30)
; (7.30) 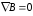 ; (7.32)
; (7.32)
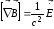 (7.31)
(7.31)  (7.33)
(7.33)
Задача
состоит в нахождении решений этих
дифференциальных уравнений, т.е.
нахождении векторов поля
 и
и
 .
.
Применим
 векторно к
(7.30) еще раз:
векторно к
(7.30) еще раз:
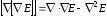 , (7.34)
, (7.34)
так
как
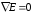 ,
то:
,
то:
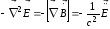 . (7.35)
. (7.35)
Используя
известную из математики связь оператора
Лапласа и оператора “набла”:
 ,
перепишем последнее уравнение в виде:
,
перепишем последнее уравнение в виде:
 . (7.36)
. (7.36)
Аналогично можно получить:
 . (7.37)
. (7.37)
Уравнения
(7.36), (7.37) называются волновыми.
Ясно, что точно такие же уравнения можно
записать для векторов
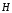 и
и
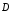 .
Зная, что:
.
Зная, что:
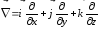 , (7.38)
, (7.38)
 , (7.39)
, (7.39)
видим, что волновые уравнения являются дифференциальными уравнениями второго порядка.
Рассмотрим
для простоты случай, когда
 и
и
 являются функциями лишь одной
пространственной координаты, например,
являются функциями лишь одной
пространственной координаты, например,
 .
Тогда (7.36):
.
Тогда (7.36):
 . (7.40)
. (7.40)
б) Плоская волна.
Решением уравнения (7.40) в общем виде является функция
 . (7.41)
. (7.41)
Это
волна, распространяющаяся вдоль оси 
 в
положительном или отрицательном
направлении. Кривая на рис.7.11, описываемая
функцией (7.41), из положения 1 спустя время
в
положительном или отрицательном
направлении. Кривая на рис.7.11, описываемая
функцией (7.41), из положения 1 спустя время
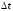 передвинется целиком на
передвинется целиком на
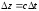 и окажется в положении 2.
Так
как в любой произвольный момент времени
значения
и окажется в положении 2.
Так
как в любой произвольный момент времени
значения
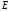 постоянны в плоскости, перпендикулярной
постоянны в плоскости, перпендикулярной
 ,
такая волна называется плоской.
,
такая волна называется плоской.
Докажем
для общей функции
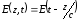 ,
что она представляет собой волну. Для
этого необходимо показать, что при
,
что она представляет собой волну. Для
этого необходимо показать, что при
 :
:
 .
.
 ,
тогда
,
тогда
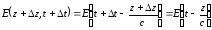 .
.
Итак,
аргумент
 отвечает волне, движущейся вдоль оси
отвечает волне, движущейся вдоль оси
 .
Точно так же можно доказать, что с
аргументом
.
Точно так же можно доказать, что с
аргументом
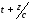 записана волна, движущаяся против
записана волна, движущаяся против
 .
.
Самым простым решением волнового уравнения является монохроматическая плоская волна:
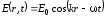 , (7.42)
, (7.42)
где

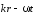 -
фаза волны,
-
фаза волны,
 ‑
волновой вектор (указывает направление
распространения волны),
‑
волновой вектор (указывает направление
распространения волны),
 ‑
радиус-вектор, проводится в точку, в
которой производится наблюдение,
‑
радиус-вектор, проводится в точку, в
которой производится наблюдение,
 - частота.
- частота.
Волна
называется монохрома-тической,
если векторы
 и
и
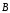 этой волны изменяются со временем по
гармоническому закону с постоянной
частотой.
этой волны изменяются со временем по
гармоническому закону с постоянной
частотой.
Фазовая скорость – скорость движения поверхности постоянной фазы (см.рис.7.12)- отвечает условию:
 =const
=const
(на
рис. - это
плоскость, перпендикулярная оси
 ,
на которой значения
,
на которой значения
 постоянны, т.е. постоянна фаза волны).
Тогда скорость движения этой плоскости
вдоль
постоянны, т.е. постоянна фаза волны).
Тогда скорость движения этой плоскости
вдоль
 может быть найдена так:
может быть найдена так:
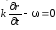
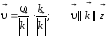 .
.
Запишем плоскую волну в комплексной форме:
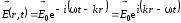 (7.43)
(7.43)
Подставив (7.43) в уравнения Максвелла, можно получить:
 ; (7.30’)
; (7.30’)
 ; (7.31’)
; (7.31’)
 . (7.33’).
. (7.33’).
 . (7.32’).
. (7.32’).
Итак:
 ; (7.44)
; (7.44) 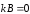 ; (7.46)
; (7.46)
 ; (7.45)
; (7.45)  . (7.47)
. (7.47)
Отсюда
следует взаимная ориентация векторов
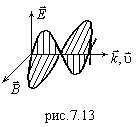
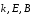 (рис.7.13):
(рис.7.13):
 ортогональны и образуют вместе с
ортогональны и образуют вместе с
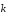 правую тройку векторов. Так как
правую тройку векторов. Так как
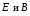 колеблются перпендикулярно
колеблются перпендикулярно
 ,
что было показано в общем виде уравнениями
(7.46) и (7.47), то полученная электромагнитная
волна поперечна.
Видно также, что волны
,
что было показано в общем виде уравнениями
(7.46) и (7.47), то полученная электромагнитная
волна поперечна.
Видно также, что волны
 синфазны.
синфазны.
Из
(7.44):
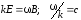 ,
тогда:
,
тогда:
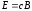 .
.
Полученная плоская электромагнитная волна приведена на рис.7.13. Итак,
решением уравнений Максвелла в вакууме является плоская монохроматическая электромагнитная волна:
 . (7.48)
. (7.48)
В
электромагнитной волне векторы
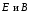 ортогональны и модули их связаны
соотношением:
ортогональны и модули их связаны
соотношением:
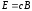 .
.
Электромагнитная
волна поперечна и векторы
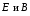 колеблются синфазно.
колеблются синфазно.
Определим вектор Умова-Пойнтинга:
 , (7.49)
, (7.49)
так
как
 .
Из (7.49) следует, что вектор
.
Из (7.49) следует, что вектор
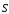 направлен так же, как
направлен так же, как
 и
и
 .
Подставим в (7.49) значения
.
Подставим в (7.49) значения
 (7.42):
(7.42):

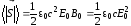 (7.50)
(7.50)
Видно из (7.50), что волна переносит энергию, т.е. она является бегущей. Скорость переноса энергии волны в вакууме равна фазовой скорости волны.
