Методичка по электричеству / Электричество лекции / 12

11

.

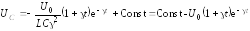Используем начальное условие:

.

Окончательно получаем:

. (6.41)

Найдем максимальное значение силы тока:

.

При

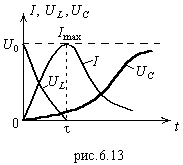
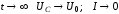. Все приведенные зависимости изображены на рис.6.13. Видно, что когда конденсатор заряжается до , ток в цепи прекращается.

Введем величину добротности контура:

(6.42).

Здесь 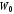- энергия, запасенная в контуре; 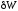‑ уменьшение энергии за период (в (6.30) считаем ).

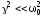Следовательно, при :

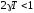. (6.43)

§ 6.3. Переменный ток.

Рассмотрим 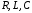- цепь с переменной ЭДС (рис.6.1). Уравнение колебательного контура:

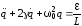. (6.44)

, (6.45)

где 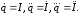При решении уравнения удобно пользоваться комплексной формой записи гармонически изменяющейся величины:

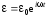. (6.46)

Сила тока также изменяется со временем по закону:

, (6.47)

где 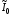- комплексная величина, в которой учитывается разность фаз между и .

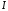Ставится задача: найти амплитудные и фазовые соотношения между током и напряжением в цепи.

Перепишем уравнение (6.45) в виде:

. (6.48)

Из (6.47) и (6.46): 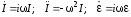. Подставим эти выражения в (6.48):

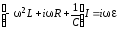. (6.49)

Разделим обе части на и учтем, что 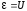. Тогда при:

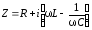(6.50)

уравнение примет вид закона Ома:

. (6.51)

Здесь - импеданс. Для переменного тока импеданс играет роль сопротивления, но из-за комплексности он позволяет учесть не только соотношения между амплитудами, но и между фазами тока и напряжений.

Для того чтобы найти соотношения между амплитудами, возьмем модули от обеих частей закона Ома (6.51):

, (6.52)

где 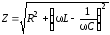. Из (6.52) получим амплитуду:

. (6.53)

Это закон Ома в вещественной форме; - омическое сопротивление; 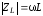- индуктивное сопротивление, а 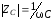- емкостное.

Для определения соотношения между фазами используем метод векторных диаграмм.

Представим комплексное число вектором на комплексной плоскости. Гармонически изменяющаяся величина изображается вектором, длина которого равна амплитуде, а угол между вектором и вещественной осью – фазой.

Из уравнения колебаний (6.49) при : 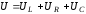, получим:

.

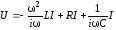Тогда:

Изобразим результаты на векторной диаграмме (рис.6.14). За начало отсчета возьмем

и направим его вдоль вещественной оси. Так же направлен и вектор тока 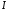(по фазе напряжение на сопротивлении совпадает с током). Теперь построим векторы , учитывая, что направлен вдоль мнимой оси, т.е. вверх, а - против мнимой оси, т.е. вниз. После этого сложим векторно 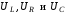и получим - приложенное напряжение. Из диаграммы рис.6.14 видно, что:

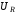а) опережает на .

б) отстает от на .

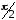в) опережает на .

Длины векторов 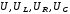- это амплитудные значения напряжений.

.

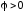Тогда . Отсюда видно, что при , или , , т.е. опережает по фазе 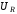и .

Таким образом, (6.47) можно записать в виде:

.

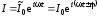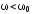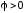Знак определяется соотношением или , соответственно: и .

К переменным токам без всякого изменения применимы первое и второе правила Кирхгофа с учетом комплексной записи закона Ома (6.51):

1) в каждом узле: ;

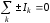2) для всякого замкнутого контура: .

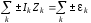При последовательном соединении импедансов: ;

при параллельном соединении импедансов: .

Величина, обратная импедансу, называется проводимостью: .

Поэтому при параллельном соединении: .

§ 6.4 Работа и мощность переменного тока.

Если в цепи имеется лишь омическое сопротивление, то мощность, рассеиваемая на этом сопротивлении, переходит в тепло:

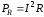. (6.54)

Индуктивные свойства цепи характеризуются , и мощность, развиваемая источником на индуктивности,

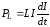. (6.55)

Ясно, что 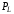может быть положительной или отрицательной в зависимости от знака . Эта мощность расходуется на энергию магнитного поля.

Если в цепи есть конденсатор, то мощность на пластинах емкости:

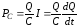. (6.56)

Она также может иметь различные знаки в зависимости от знака , превращаясь в энергию электрического поля.

Общая мощность:

;

Начиная отсчет фазы от (или ) с учетом сдвига фаз можно записать:

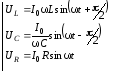
Тогда при :

(6.57).

Такие мощности называются мгновенными, ибо формулы верны при любом . Для получения средней мощности за период необходимо усреднить эти выражения. С учетом того, что:

,

найдем:

.

Поэтому - активное сопротивление, так как выделяемая на нем средняя мощность отлична от нуля; 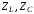 ‑ реактивные сопротивления.

Мгновенная мощность, выделяемая в цепи:

Тогда средняя мощность:

. (6.58)

Из векторной диаграммы рис.6.15 видно, что , следовательно:

,

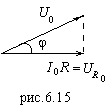
где 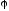- разность фаз между и 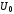. Это выражение совпадает с (6.58). Множитель называется коэффициентом мощности. Формулу для 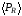можно сделать идентичной формуле для постоянного тока, если ввести обозначения:

. (6.59)

Эти формулы легко получить как среднеквадратичные по периоду значения:

.

Данные значения называются действующими (эффективными). Все приборы отградуированы на эти значения.

.

При , , каковы бы ни были значения 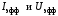. В этом случае энергия, передаваемая от источника во внешнюю цепь, в точности равна за период энергии, возвращаемой из внешней цепи в источник. Вся энергия бесполезно колеблется между источником и внешней цепью.

Мощность, потребляемая во внешней цепи, максимальна при . Из формулы для ясно, что если общее реактивное сопротивление велико по сравнению с активным: , то также велико. Значит, нужно сделать реактивное сопротивление как можно меньше: 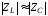, чтобы коэффициент мощности был порядка единицы и потребляемая мощность была максимальной.

§ 6.5. Резонансы в цепях переменного тока.

1. Резонанс напряжений.

Рассмотрим - цепь с элементами, включенными последовательно (рис.6.1). Векторная диаграмма тока и напряжений такой цепи приведена на рис.6.14, откуда:

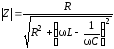; (6.60)

. (6.61)

Из диаграммы рис.6.14 и формулы (6.61) видно, что при 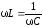, ; ; 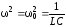. При таком условии получено максимальное значение тока, что эквивалентно условию:

. (6.62)

При этом , т.е. , где 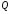 - добротность контура (6.43); при малом затухании 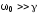: 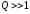, т.е. при резонансе и в раз больше, чем .

Исследуем зависимости 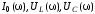. Для этого преобразуем формулы следующим образом. Ток в цепи:

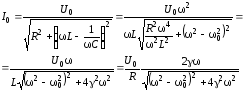(6.63)

Напряжение на элементах цепи:

; (6.64)

; (6.65)

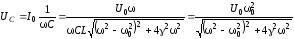. (6.66)

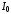Зависимость угла - разности фаз между и 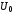- от частоты:

. (6.67)

Графические зависимости (6.64) и (6.67) представлены на рис.6.16 (а и б, соответственно).

Достигают ли максимума и при каких частотах?

Условие отвечает минимуму знаменателя (6.66).

. (6.68)

Продифференцировав, получаем: , откуда:

или:

. (6.69)

Максимальное значение 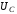при этом:

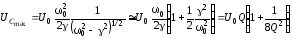. (6.70)

При совпадении частоты вынужденных колебаний и собственной частоты наблюдается резонанс: .

При

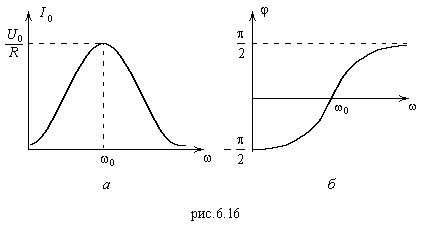
Найдем условие максимума .

.

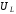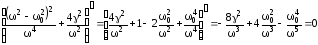Упростим: 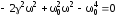, откуда:

. (6.71)

Значение 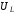при этом:

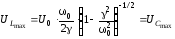. (6.72)

При .

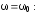
При

Таким образом, достигают максимума при частотах, не равных . Оценим, насколько велико это отличие. Так, при : ; .

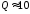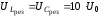Графики частотной зависимости (6.64), (6.65) и (6.66) приведены на рис.6.17. Из графиков видно, что если выходным сигналом является

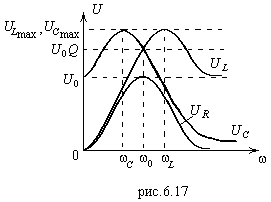
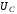, то контур служит для ослабления высоких частот (высокочастотный фильтр –ВЧ-фильтр). Если же на выходе снимается 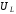, то ослабляется низкочастотная часть, и контур служит низкочастотным фильтром (НЧ-фильтром).

Оценим отличие 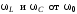по (6.69) и (6.71).

Для 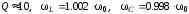. Следовательно, при большой добротности, т.е. при малом затухании, можно считать, что максимумы 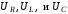совпадают по частоте. Величины максимумов в раз больше, чем .
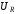