Методичка по электричеству / Электричество лекции / 14

7

Глава 7. Уравнения Максвелла. Электромагнитные волны.

§ 7.1. Ток смещения.

Понятие “тока смещение” впервые было введено Максвеллом.

Сущность явления заключается в следующем. Постоянный ток не протекает в цепи с конденсатором. Переменный ток течет в такой цепи. Сила тока во всех последовательно соединенных элементах такой цепи одна и та же. В то же время, в конденсаторе ток проводимости, связанный с движением электронов, не может существовать, поскольку обкладки разделены диэлектриком. Поэтому в конденсаторе должен проходить какой – то процесс, который замыкает ток проводимости, текущий во всей остальной цепи. Этот процесс обеспечивает обмен зарядом между обкладками без переноса заряда между ними. Этот процесс называется током смещения.

Необходимость процесса, замыкающего ток проводимости в конденсаторе, хорошо видна при использовании закона полного тока в такой цепи в дифференциальной форме:

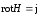. (7.1)

Возьмем операцию 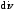от обеих частей (7.1) с учетом того, что (см. Приложение, формулы (7)):

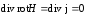. (7.2)

А выражение 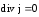- условие замкнутого контура тока.

Рассмотрим цепь переменного тока с плоским конденсатором (рис.7.1). Между обкладками сосредоточено электрическое поле

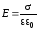, где - плотность заряда на обкладках, - диэлектрическая проницаемость вещества между обкладками. Вектор электрической индукции между обкладками: 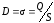, где 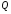- заряд на каждой из обкладок. Сила тока в цепи: 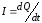. Отсюда:

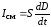, (7.3)

т.е. процесс, замыкающий ток проводимости в цепи с конденсатором, связан с изменением электрической индукции между обкладками конденсатора (иное название вектора 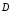- вектор электрического смещения). Плотность тока смещения:

. (7.4)

Это локальное соотношение, т.е. выполняется оно не только для плоского конденсатора.

Для того чтобы придать этому названию физический смысл, необходимо доказать, что 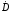обладает свойствами тока, хотя и не представляет движение электрических зарядов.

Главным свойством тока является его способность порождать магнитное поле. Поэтому решающим является вопрос о том, порождает ли ток смещения магнитное поле так же, как ток проводимости.

Если применить закон полного тока, то циркуляция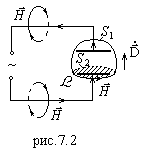

по контуру L равна 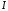(рис.7.2). Перемещая контур вдоль цепи, видим, что циркуляция не должна изменяться и тогда, когда контур охватывает конденсатор. Для доказательства натянем на конденсатор поверхность в виде сферы, разрежем ее плоскостью снизу внутри конденсатора и по месту разреза проведем контур L. Поверхност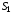и и 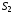натянуты на один и тот же контур L. Через 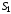течет ток, а через 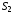в отсутствие тока смещения ток не течет. Получается, что в одном случае 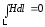, а в другом: 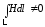. В целях избежания этого противоречия вводится 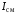в конденсаторе, который создает поле 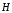, так как .

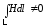Следовательно, ток смещения порождает в конденсаторе такое же магнитное поле, как ток проводимости. Экспериментально это проверяется с помощью пояса Роговского.

Рассмотрим, к чему это приводит с точки зрения уравнений Максвелла. Теорема о циркуляции записывается в виде (7.1). Учитывая ток смещения, нужно записать:

или 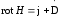. (7.5)

Это означает, что магнитное поле порождается не только током проводимости, но и переменным электрическим полем.

Физическое содержание уравнения (7.5) иллюстрирует рис.7.3. Рис.7.3, а – случай когда имеется лишь ток проводимости, который определяет магнитное поле. Рис.7.3, б изображает общий случай, когда ток проводимости и ток смещения вместе создают магнитное поле. Рис.7.3, в -случай, когда не существует тока проводимости (вакуум), а магнитное поле создается изменением электрического поля.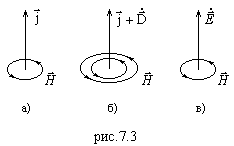

Ситуация здесь аналогична той, которая рассматривалась в связи с законом электромагнитной индукции (иллюстрирует рис.7.4):

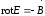. (7.6)

Следует обратить внимание на противоположные направления векторов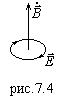

и при одинаковых направлениях 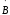и 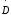из-за знака “‑“ в (7.6).

Таким образом, взаимное порождение электрического и магнитного полей – фундаментальный закон.

Рассмотрим примеры для оценки величины .

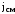Задача 1.

Между двумя концентрическими металлическими сферами находится слабо проводящий диэлектрик (проницаемость , проводимость ). Внутренняя сфера заряжена зарядом . Найти ток смещения через произвольную замкнутую поверхность внутри между сферами.

Полный ток смещения через поверхность согласно (7.4):

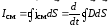. (7.7)

По теореме Гаусса: 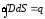, т.е. 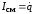. Согласно закону сохранения заряда (уравнение непрерывности):

.

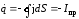Тогда: 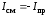, т.е. ток смещения между обкладками равен току проводимости - току утечки с противоположным знаком. Используя закон Ома 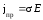и теорему Гаусса для 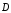, запишем:

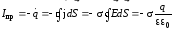(7.8)

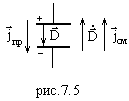
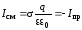(7.9)

Иллюстрация (7.9) - на рис.7.5, из которого видно, что: .

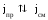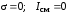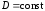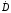Для , поскольку и =0.

Задача 2.

Длинный прямой соленоид радиуса R имеет n - витков на единицу длины. По нему течет ток 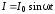. Найти плотность тока смещения в зависимости от расстояния до оси соленоида.

.

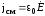Найдем электрическое поле по закону электромагнитной индукции: , ; .

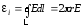Для .

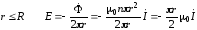, так как в знаменателе стоит множитель .

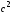Для .

.

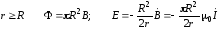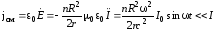Введем величину

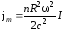и приведем зависимость на рис.7.6. Для .

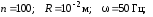
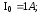
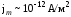В случае быстропеременных процессов ток смещения может достигать больших значений, становясь сравнимым с током проводимости.

§ 7.2. Система уравнений Максвелла.

Теперь можно все свойства (законы) магнитного и электрического полей записать в виде системы уравнений Максвелла. В дифференциальной форме:

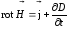(7.11) 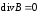(7.13);

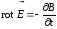(7.12) 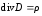(7.14).

Это полевые уравнения, применимые для описания электромагнитных явлений. В дополнение к ним следует записать материальные уравнения:

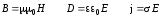. (7.15).

Уравнения Максвелла в виде (7.11-7.15) были записаны Хевисайдом. Считая математику “служанкой” техники, Хевисайд часто предлагал формулы без математического доказательства. Им же был разработан без строгого доказательства операторный метод; открыт слой Хевисайда, полностью отражающий короткие волны.

Обратим внимание на то, что уравнения (7.13) и (7.14) являются дифференциальным следствием (7.12), (7.11). Для доказательства применим операцию 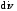к (7.12):

.

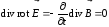Но так как , то 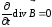, что совпадает с продифференцированным по времени уравнением (7.13).

Применим теперь операцию 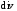к (7.11):

.

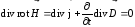Тогда 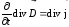. Учтем уравнение непрерывности:

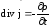
и получим: 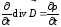и , что совпадает с продифференцированным по времени уравнением (7.14).

Это означает, что система уравнений Максвелла не переполнена. В ней содержится 8 скалярных уравнений и 6 неизвестных компонент векторов 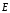и .

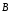Физический смысл уравнений Максвелла:

• (7.11). Источником магнитного поля являются ток проводимости и переменное электрическое поле.

• (7.12). Источником электрического поля 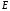являются неподвижные электрические заряды (при этом поле потенциально) и переменное магнитное поле (при этом электрическое поле является вихревым).

• (7.13). Не существует магнитных зарядов; силовые линии магнитного поля являются замкнутыми; поле является вихревым.

• (7.14). Потенциальное электрическое поле имеет источником неподвижные заряды, силовые линии вектора электрического смещения начинаются на 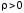и заканчиваются на зарядах .

Уравнения Максвелла и материальные уравнения дополняются формулой для плотности энергии электромагнитного поля:

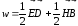. (7.16)