
§ 2.5. Энергия электростатического поля.
Поместим
точечный источник – заряд
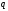 в поле потенциала
в поле потенциала
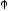 .
Так как
.
Так как
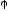 - это работа по перемещению положительного
единичного заряда из 1 на бесконечность,
то:
- это работа по перемещению положительного
единичного заряда из 1 на бесконечность,
то:
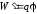 - (2.42)
- (2.42)
энергия
заряда
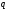 в поле
в поле
 .
.
Для
двух точечных зарядов
 и
и
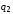 работа при перемещении их от
работа при перемещении их от
 до бесконечности определяет потенциальную
энергию:
до бесконечности определяет потенциальную
энергию:
 , (2.43)
, (2.43)
где
 и
и
 - потенциалы, создаваемые первым! и
вторым зарядом!, соответственно, в месте,
где помещены
- потенциалы, создаваемые первым! и
вторым зарядом!, соответственно, в месте,
где помещены
 и
и
 .
Для случая нескольких точечных зарядов:
.
Для случая нескольких точечных зарядов:
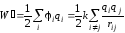 . (2.44)
. (2.44)
Это энергия взаимодействия системы дискретных зарядов.
Рассмотрим
теперь случай, когда заряды распределены
непрерывно. Зная, что
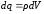 ,
и переходя от суммирования к интегрированию,
получаем:
,
и переходя от суммирования к интегрированию,
получаем:
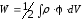 , (2.45)
, (2.45)
где
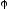 - потенциал, создаваемый всеми зарядами
системы в элементе
- потенциал, создаваемый всеми зарядами
системы в элементе
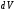 .
Это выражение кажется простым обобщением
предыдущей формулы, но это не так – они
различны, поскольку
.
Это выражение кажется простым обобщением
предыдущей формулы, но это не так – они
различны, поскольку
 ,
входящий в формулы (2.44)
и (2.45), имеет разный смысл.
,
входящий в формулы (2.44)
и (2.45), имеет разный смысл.
Для
объяснения рассмотрим следующий пример.
Пусть система состоит из двух шаров с
зарядами
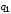 и
и
 .
Расстояние между ними много больше их
размеров, т.е.
.
Расстояние между ними много больше их
размеров, т.е.
 и
и
 - точечные заряды. Энергия системы имеет
вид (2.43), где
- точечные заряды. Энергия системы имеет
вид (2.43), где
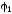 -
потенциал,
создаваемый
-
потенциал,
создаваемый
 в точке, где помещен
в точке, где помещен
 ,
потенциал
,
потенциал
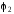 создан
создан
 в точке, где помещен
в точке, где помещен
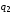 .
.
Воспользуемся
теперь формулой (2.45). Интеграл должен
разбиться на два по объемам
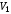 и
и
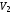 :
:
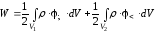 . (2.46)
. (2.46)
Разобъем
заряд первого шара на элементарные
 .
На этот заряд действует потенциал,
создаваемый всеми зарядами второго
шара и, кроме того, зарядами собственного
шара:
.
На этот заряд действует потенциал,
создаваемый всеми зарядами второго
шара и, кроме того, зарядами собственного
шара:
 (2.47).
(2.47).
То же самое и для элементарного заряда второго шара. Действующий на него потенциал:
 . (2.48)
. (2.48)
С учетом (2.47) и (2.48) можно (2.46) записать:
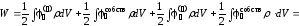
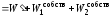 , (2.49)
, (2.49)
где
 - энергия взаимодействия шаров зарядами
- энергия взаимодействия шаров зарядами
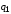 и
и
 ;
;
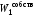 и
и
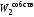 - собственные энергии этих шаров.
- собственные энергии этих шаров.
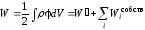 . (2.50)
. (2.50)
Это
формула для системы из
 -
шаров. Она содержит энергию взаимодействия
зарядов шаров и собственные энергии.
-
шаров. Она содержит энергию взаимодействия
зарядов шаров и собственные энергии.
Теперь
получим формулу (2.45), но не при наличии
потенциала, а в присутствии
электростатического поля. Рассмотрим
это на примере плоского конденсатора
и его энергии. Для начала выведем
выражение для энергии уединенного
проводника, имеющего заряд
 и потенциал
и потенциал
 .
Поскольку
.
Поскольку
 во всех точках проводника одинаков,
вынесем его за знак интеграла в формуле
(2.45). Тогда оставшийся интеграл – это
заряд
во всех точках проводника одинаков,
вынесем его за знак интеграла в формуле
(2.45). Тогда оставшийся интеграл – это
заряд
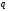 на проводнике;
на проводнике;
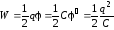 .
.
Теперь
рассмотрим энергию конденсатора, где
 и
и
 - заряд и потенциал положительно
заряженной обкладки,
- заряд и потенциал положительно
заряженной обкладки,
 и
и
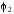 - то же для отрицательно заряженной
обкладки. Так как
- то же для отрицательно заряженной
обкладки. Так как
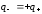 ,
то:
,
то:
 .
.
Учтем,
что  .
Тогда:
.
Тогда:
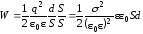 . (2.51)
. (2.51)
Подставив:
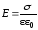 ;
;  ;
; 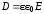 ,
получим:
,
получим:
 - (2.52)
- (2.52)
электрическая
энергия конденсатора. Плотность энергии
с учетом того, что
 и
и
 -
векторы:
-
векторы:
 . (2.53)
. (2.53)
Видно, что носителем энергии является поле, и энергия локализована во всем пространстве, где есть электрическое поле. Так как:
 ,
,
то
 - плотность энергии положительна.
- плотность энергии положительна.
Для
общего случая, когда
 изменяется в пространстве:
изменяется в пространстве:
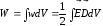 . (2.54)
. (2.54)
Сравним формулы (2.45) и (2.54). В первой носителями энергии являются заряды, и энергия локализована на зарядах. В (2.54) носителем энергии является поле, и энергия локализована во всем пространстве, где имеется поле.
Обе
формулы представляют полную энергию,
включающую энергию взаимодействия и
собственную энергию.
Покажем
это для (2.54)
на примере двух заряженных тел в пустоте,
создающих в пространстве поля
 и
и
 ,
соответственно. По принципу суперпозиции:
,
соответственно. По принципу суперпозиции:
 ,
,
 .
.
Полная энергия системы:
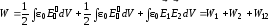 ,
(2.55)
,
(2.55)
где
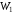 и
и
 - собственные энергии первого и второго
тел,
- собственные энергии первого и второго
тел,
 -
энергия их взаимодействия.
-
энергия их взаимодействия.
 и
и
 всегда положительны,
всегда положительны,
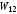 может быть как положительной, так и
отрицательной. Полная энергия
может быть как положительной, так и
отрицательной. Полная энергия
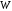 также всегда положительна. Если в формулу
(2.53)
подставить
также всегда положительна. Если в формулу
(2.53)
подставить
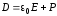 ,
тогда:
,
тогда:
 . (2.56)
. (2.56)
Первое слагаемое – это плотность энергии поля в вакууме. Второе – плотность энергии, связанная с поляризацией диэлектрика.
Пример.
1.
Определить
энергию
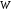 объемно заряженного шара. Даны
объемно заряженного шара. Даны
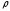 и
и
 .
.
Согласно (1.24) и (1.25) примера 3 §1.4:
для 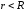 :
:
 ; для
; для  :
:
 ;
;
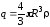 ;
;
 .
.
Найдем теперь полную энергию по формуле (2.54):

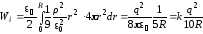 .
.
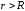
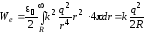 .
.
Видно,
что  .
.
Полная энергия:
 . (2.57)
. (2.57)
2. Энергия диполя во внешнем поле.
Поле
создают потенциалы
 в точках, где расположены заряды
в точках, где расположены заряды
 (см.рис.2.20).
Тогда энергия этих зарядов по (2.42)
равняется:
(см.рис.2.20).
Тогда энергия этих зарядов по (2.42)
равняется:
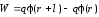 .
.
Так
как
 ,
разложим
,
разложим
 в
ряд:
в
ряд:
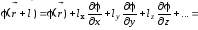
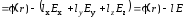 , (2.58)
, (2.58)
где
 - компоненты
- компоненты
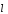 ;
;
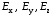 - компоненты
- компоненты
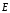 .
.
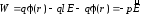 . (2.59)
. (2.59)
Из
(2.59)
видно, что в поле
 диполь ориентируется так, что
диполь ориентируется так, что
 (минимум энергии). Рассмотрение механизма
поворота вектора
(минимум энергии). Рассмотрение механизма
поворота вектора
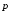 связано с появлением вращающего момента,
так как на заряды
связано с появлением вращающего момента,
так как на заряды
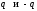 со стороны поля
со стороны поля
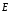 действуют противоположно направленные
силы
действуют противоположно направленные
силы
 .
.
§ 2.6. Силы в электрическом поле.
Природа всех этих сил - силы, действующие на заряд. Поэтому рассмотрим отдельно силы, действующие на точечный заряд, диполь, систему диполей.
-
Силы, действующие на точечный заряд.
Согласно (1.5):
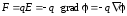 . (2.60)
. (2.60)
Для непрерывно распределенного заряда:
 . (2.61)
. (2.61)
Объемная плотность сил:
 . (2.62)
. (2.62)
-
Сила, действующая на диполь.
Внешнее
поле
 в точках (см.рис.2.20)
в точках (см.рис.2.20)
 и
и
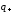
 и
и
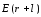 ,
где О –
начало координат,
,
где О –
начало координат,
 - радиусы
- векторы
точек
- радиусы
- векторы
точек
 и
и
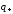 .
Вследствие принципа суперпозиции для
диполя сила со стороны электрического
поля равна:
.
Вследствие принципа суперпозиции для
диполя сила со стороны электрического
поля равна:
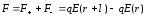 .
.
Для
диполя выполняется соотношение
 ,
поэтому для функции
,
поэтому для функции
 справедливо следующее разложение в
ряд:
справедливо следующее разложение в
ряд:
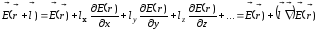 ,
,
где

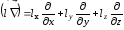 .
Таким образом:
.
Таким образом:
 . (2.63)
. (2.63)
В
однородном поле
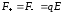 ,
,
 .
Однако,
остается вращающий момент:
.
Однако,
остается вращающий момент:
 , (2.64)
, (2.64)
ориентирующий
 .
.
-
Сила, действующая на диэлектрик.
На
объем
 диэлектрика
действует сила:
диэлектрика
действует сила:
 , (2.65)
, (2.65)
суммирование проводится по элементарным диполям в объеме.
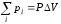 ; (2.66)
; (2.66)
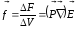 , (2.67)
, (2.67)
где
 - объемная плотность сил (или сила,
действующая на единицу объема). Так как
- объемная плотность сил (или сила,
действующая на единицу объема). Так как
 ,
то:
,
то:
 , (2.68)
, (2.68)
где
учтено
(см.
Приложение, формулу (2)), что:
 и теорема о циркуляции, согласно которой
и теорема о циркуляции, согласно которой
 .
.
Сила,
действующая на единицу объема диэлектрика,
пропорциональна градиенту от квадрата
напряженности поля и направлена в
сторону увеличения абсолютного значения
 .
.
Применим
эти формулы для нахождения сил, действующих
на шар из диэлектрика (см. рис. 2.21),
находящийся в однородном электрическом
поле для двух случаев: 
 и
и
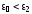 .
Для
применения формулы
(2.68)
необходимо считать, что переход от
внешней области с диэлектрической
проницаемостью
.
Для
применения формулы
(2.68)
необходимо считать, что переход от
внешней области с диэлектрической
проницаемостью
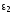 к
внутренней с
к
внутренней с
 совершается
не скачком
на
поверхности
шара,
а непрерывно в тонком сферическом слое.
В этом слое напряженность
совершается
не скачком
на
поверхности
шара,
а непрерывно в тонком сферическом слое.
В этом слое напряженность
 изменяется
от ее значения вне шара до значения
внутри шара. В случае
изменяется
от ее значения вне шара до значения
внутри шара. В случае
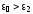 напряженность поля внутри шара меньше,
чем вне шара. Поэтому сила направлена
во внешнюю сторону шара. В случае
напряженность поля внутри шара меньше,
чем вне шара. Поэтому сила направлена
во внешнюю сторону шара. В случае
 силы направлены внутрь шара. В первом
случае силы стремятся растянуть шар
вдоль линий напряженности поля. Во
втором – сплющить его. Это явление
называется стрикцией.
силы направлены внутрь шара. В первом
случае силы стремятся растянуть шар
вдоль линий напряженности поля. Во
втором – сплющить его. Это явление
называется стрикцией.
-
Поверхностные силы.
На
границе диэлектрика нормальная
составляющая
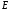 претерпевает скачок, т.е. имеется градиент
поля, и возникают поверхностные силы.
Выражение для них легко получить в
простом случае расслоенного конденсатора.
претерпевает скачок, т.е. имеется градиент
поля, и возникают поверхностные силы.
Выражение для них легко получить в
простом случае расслоенного конденсатора.
А) Конденсатор с продольно расслоенным диэлектриком.
Рассмотрим
заряды, возникающие на границе диэлектрика
с обкладками и на границе между
диэлектриками
(см.рис.2.22).
Ясно
(см.(2.40)),
что если учесть 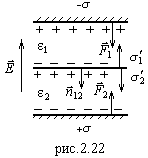
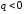 (верхняя
пластина конденсатора), то:
(верхняя
пластина конденсатора), то:
 ,
,  ,
,
 ;
;
 ,
, 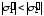 ,
,
 .
.
Теперь
рассмотрим силы
 ,
действующие на обкладки конденсатора.
Для их нахождения учтем, что работа сил,
действующих на обкладки, должна быть
равна убыли энергии электрического
поля конденсатора. Если первую обкладку
сместить на
,
действующие на обкладки конденсатора.
Для их нахождения учтем, что работа сил,
действующих на обкладки, должна быть
равна убыли энергии электрического
поля конденсатора. Если первую обкладку
сместить на
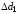 ,
то:
,
то:
 ,
,  .
.
Также
и  .
.
Энергия конденсатора и емкость его запишутся:
 ;
; 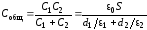 .
.
Тогда:
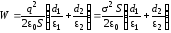 (2.69).
(2.69).
Можно найти силы и изобразить соответствующие некоторые на рис.2.22:
 ;
;  . (2.70)
. (2.70)
Теперь рассмотрим силы на границе диэлектриков. Энергия каждого конденсатора:
 ;
;  . (2.71)
. (2.71)
Силы на границе:
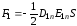 ;
;  . (2.72)
. (2.72)
Направления сил показаны на рис.2.22, они определяются знаками зарядов на концах диэлектриков 1 и 2. Сила на обкладке (2.70) равна силе на границе диэлектрика (2.72):

(при
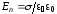 на поверхности металла
(см. (2.6)):
на поверхности металла
(см. (2.6)):
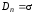 ),
но их направления противоположны.
Равнодействующая
двух сил, приложенных к границе:
),
но их направления противоположны.
Равнодействующая
двух сил, приложенных к границе:
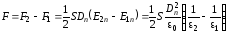 , (2.73)
, (2.73)
где
учтено, что при отсутствии сторонних
зарядов на границе
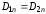 .
Сила, действующая на единицу поверхности
равна разности плотностей энергии
электрического поля по обе стороны
границы:
.
Сила, действующая на единицу поверхности
равна разности плотностей энергии
электрического поля по обе стороны
границы:
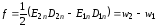 . (2.74)
. (2.74)
Направление

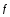 зависит
от соотношения
зависит
от соотношения
 .
Из (2.73)
видно, что при
.
Из (2.73)
видно, что при

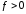 ,
т.е.
,
т.е.
 ,
,
 .
Сила на границе диэлектриков направлена
в сторону диэлектрика с меньшим
.
Сила на границе диэлектриков направлена
в сторону диэлектрика с меньшим
 ,
или в сторону с большей объемной
плотностью энергии поля.
,
или в сторону с большей объемной
плотностью энергии поля.
Полученная
сила называется максвелловским
натяжением;
как видно из рис.2.23, силы
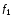 и
и
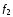 как бы растягивают поверхность границы.
как бы растягивают поверхность границы.
Б) Конденсатор с поперечно расслоенным диэлектриком.
На
границе двух диэлектриков диполи
отталкиваются, что приводит к
соответствующим направлением сил (см.
рис.2.24). 
Так как напряженность поля направлена вдоль границы, то справедливы следующие условия на границе:
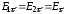 .
.
Соответственно, выражения (2.71) для энергии перепишутся в виде:
 ; (2.75)
; (2.75)
где
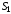 и
и
 - площади диэлектриков, прилегающих к
обкладкам;
- площади диэлектриков, прилегающих к
обкладкам;
 ,
,
 ,
где
,
где
 - ширина конденсатора, взятая вдоль
- ширина конденсатора, взятая вдоль
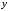 .
Учтем, что:
.
Учтем, что:
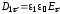
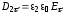 .
.
Тогда (2.75) перепишется в виде:
 .
(2.76)
.
(2.76)
Разность плотностей энергии:
 . (2.77)
. (2.77)
Если
находить
 и
и
 по формулам (2.76)
и
по формулам (2.76)
и
 ,
,
 ,
а затем применить принцип суперпозиции
,
а затем применить принцип суперпозиции
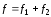 ,
то легко видеть, что равнодействующая
сил, приложенных к поверхности
по
разные стороны границы:
,
то легко видеть, что равнодействующая
сил, приложенных к поверхности
по
разные стороны границы:
 , (2.78)
, (2.78)
сила
равна разности плотностей энергий и
направлена в сторону диэлектрика с
меньшим
 .
.
Это
видно из следующего:
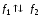 ;
;

 .
.
Если
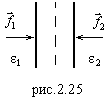
 ,
то сила
,
то сила
 должна быть направлена в ту же сторону,
что и
должна быть направлена в ту же сторону,
что и
 (т.е.
(т.е.
 ),
а вектор
),
а вектор
 направлен в сторону диэлектрика с
направлен в сторону диэлектрика с
 .
Эта сила называется максвелловским
давлением. Как
показано
на
рис.2.25,
электрическое
поле как бы давит на поверхность раздела.
.
Эта сила называется максвелловским
давлением. Как
показано
на
рис.2.25,
электрическое
поле как бы давит на поверхность раздела.
