
- •Глава 4. Линейные дифференциальные уравнения и системы
- •1. Общие замечания. Однородные и неоднородные уравнения и системы
- •2. Фундаментальная система решений однородной системы м однородного уравнения
- •3. Дифференцирование векторов, матриц, определителей. Комплекснозначные функции действительного аргумента
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4.Определитель Вронского
- •5. Метод вариации постоянных для неоднородных уравнений и систем
- •6. Однородные уравнения с постоянными коэффициентами
- •Типовые задачи
- •Задачи для самостоятельного решения
- •7. Линейные однородные системы с постоянными коэффициентами
- •Типовые задачи
- •Задачи для самостоятельного решения
- •8. Линейные неоднородные уравнения и системы с постоянными коэффициентами со специальной правой частью
- •Типовые задачи
- •Задачи для самостоятельного решения
Типовые задачи
Найти все решения системы
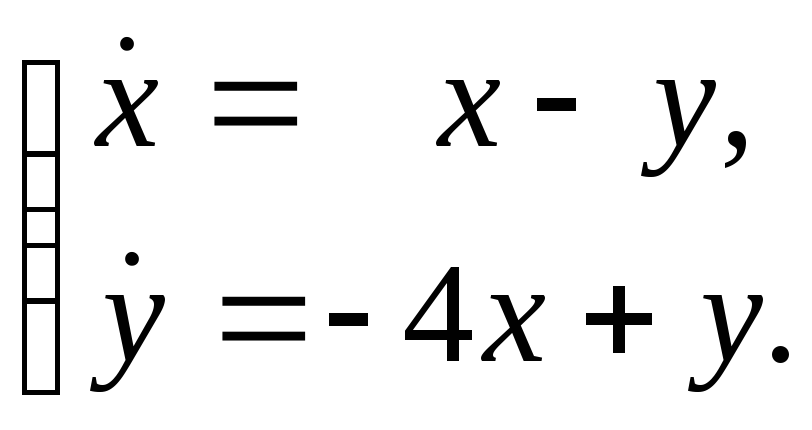
Решение.
Составим характеристическое уравнение:
![]() Его корни:
Его корни:![]()
![]() Найдём собственные векторы из системы
Найдём собственные векторы из системы![]() Для
Для![]() имеем:
имеем: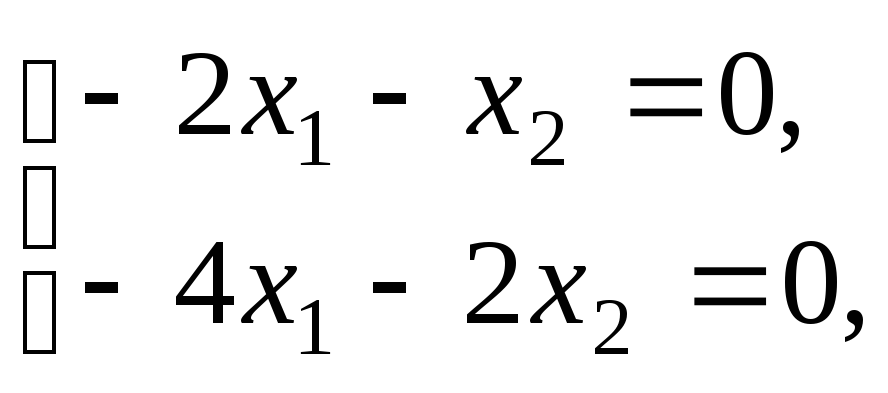 откуда
откуда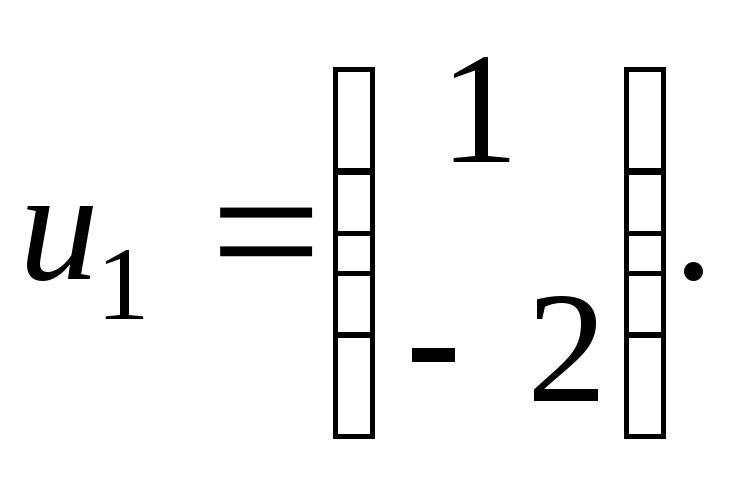
Для
![]() имеем:
имеем: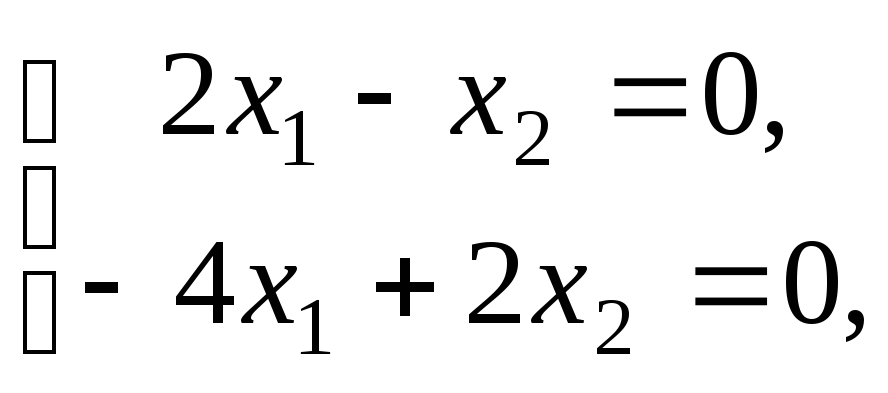 откуда
откуда
Таким образом, общее решение системы имеет вид

Найти решение системы
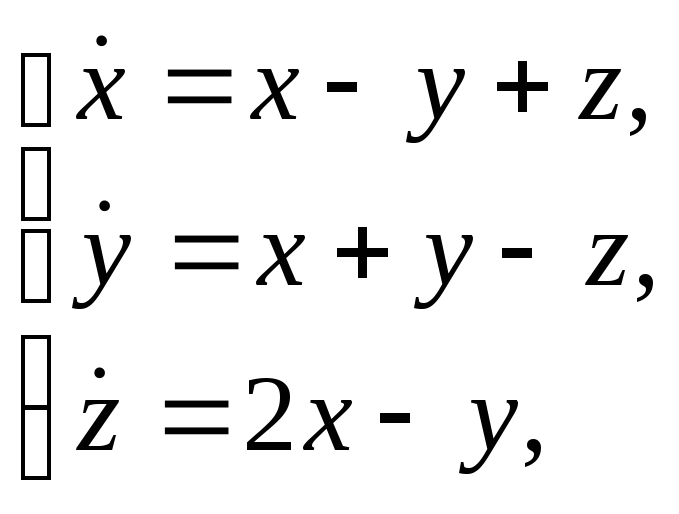
удовлетворяющее
начальному условию
![]()
Решение.
Характеристическое уравнение
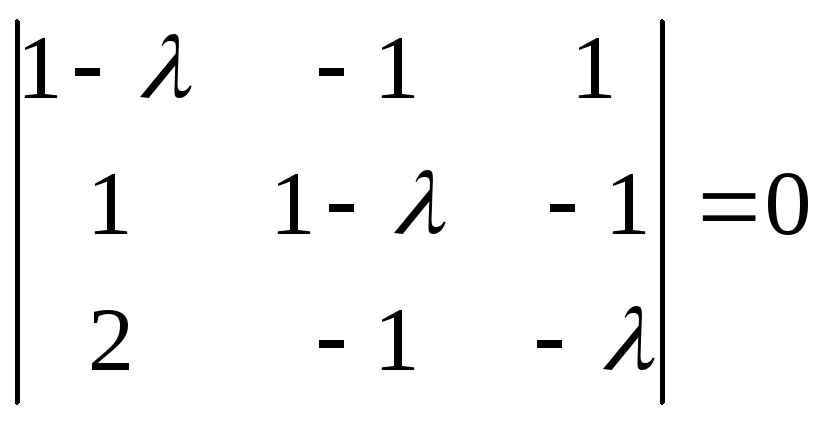 имеет корни
имеет корни![]()
![]()
![]() Для
Для![]() имеем систему
имеем систему Её ненулевое решение:
Её ненулевое решение: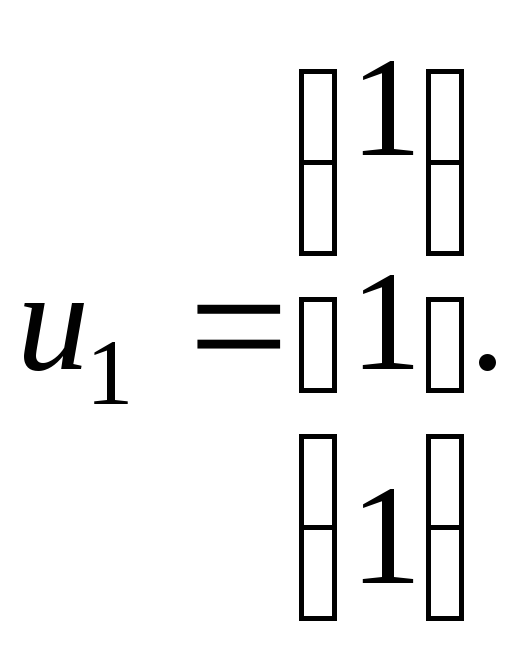 Для
Для![]() имеем систему
имеем систему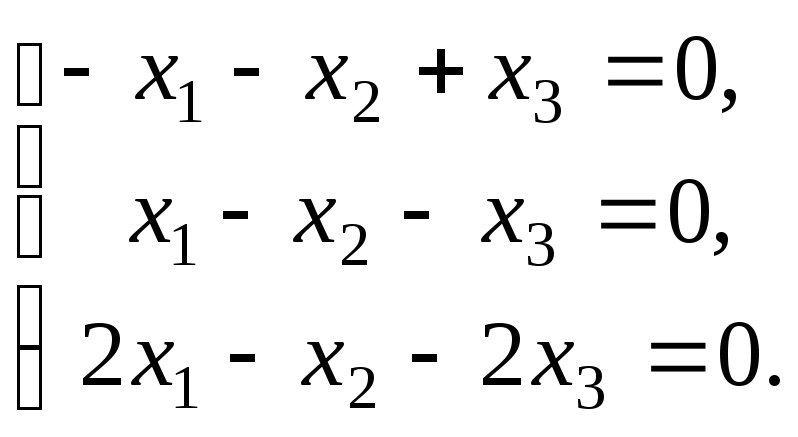 Её ненулевое решение:
Её ненулевое решение: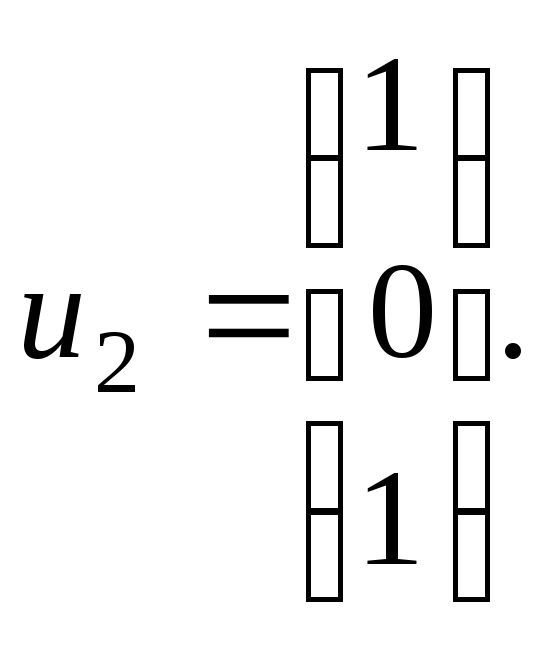 Наконец, для
Наконец, для![]() имеем:
имеем: Её ненулевое решение:
Её ненулевое решение: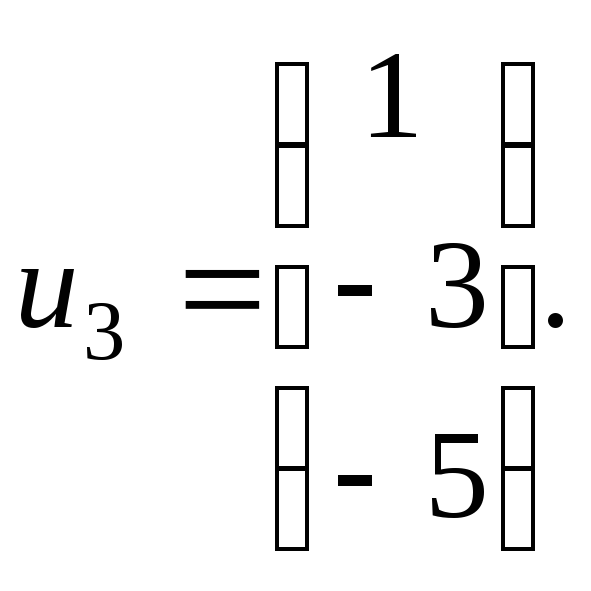 Таким образом, общее решение системы
имеет вид
Таким образом, общее решение системы
имеет вид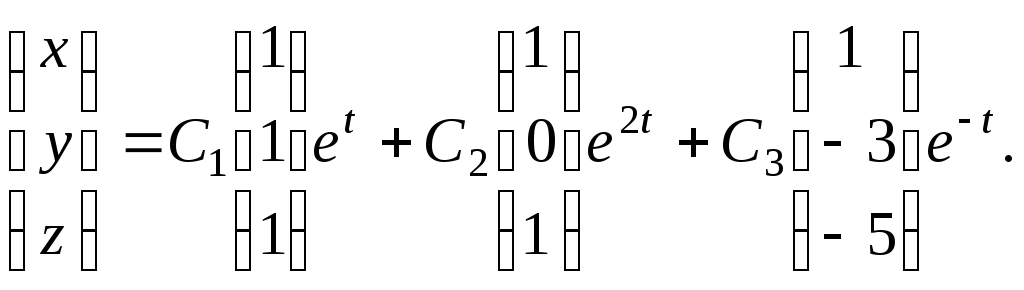 Подставим в это равенство
Подставим в это равенство![]() и воспользуемся начальным условием.
Тогда будем иметь
и воспользуемся начальным условием.
Тогда будем иметь
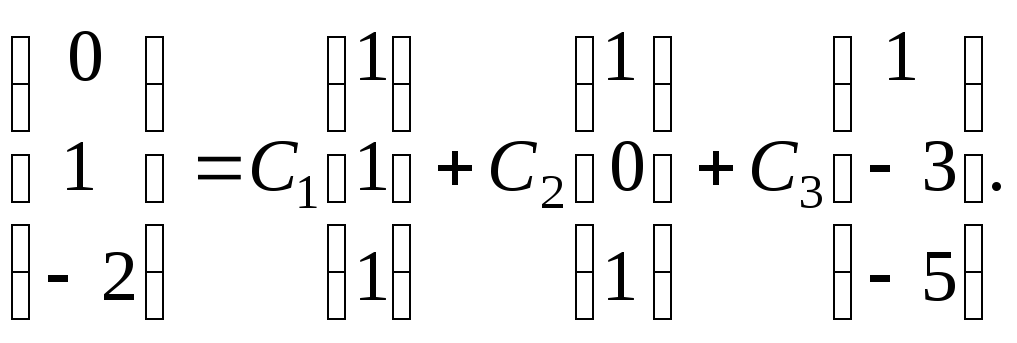
Мы
получили систему уравнений для нахождения
![]() Решив её, получим:
Решив её, получим:![]()
![]()
![]() Отсюда получаем окончательный ответ:
Отсюда получаем окончательный ответ:
![]()

Решить уравнение
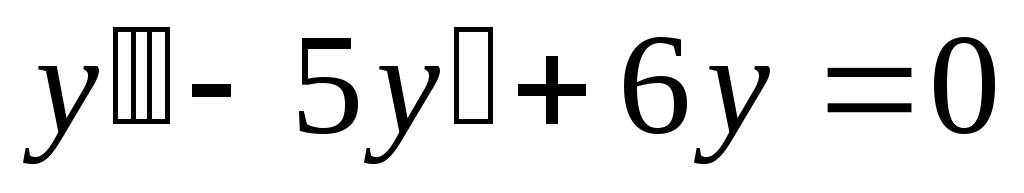 двумя способами: а) непосредственно и
б) сведением к системе. Сравнить
полученные решения.
двумя способами: а) непосредственно и
б) сведением к системе. Сравнить
полученные решения.
Решение.
Сначала решим это уравнение непосредственно.
Составим характеристическое уравнение:
![]() Его корни:
Его корни:![]()
![]() Следовательно, общее решение уравнения
имеет следующий вид:
Следовательно, общее решение уравнения
имеет следующий вид:![]()
Теперь
сведём это уравнение к системе. Положим
![]()
![]() Тогда
Тогда![]() Значит, наше уравнение эквивалентно
системе
Значит, наше уравнение эквивалентно
системе Матрица этой системы:
Матрица этой системы:![]() Характеристическое уравнение:
Характеристическое уравнение:![]() Нетрудно видеть, что это уравнение
совпадает с характеристическим
уравнением, написанным ранее для
дифференциального уравнения. Для каждого
из корней характеристического уравнения
найдём соответствующий ему собственный
вектор. Если
Нетрудно видеть, что это уравнение
совпадает с характеристическим
уравнением, написанным ранее для
дифференциального уравнения. Для каждого
из корней характеристического уравнения
найдём соответствующий ему собственный
вектор. Если![]() то мы получаем систему
то мы получаем систему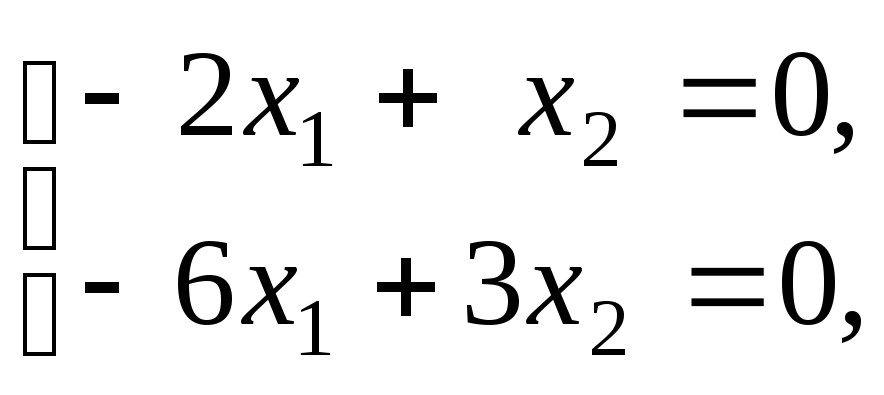 из которой находим собственный вектор
из которой находим собственный вектор Для корня
Для корня![]() получаем систему
получаем систему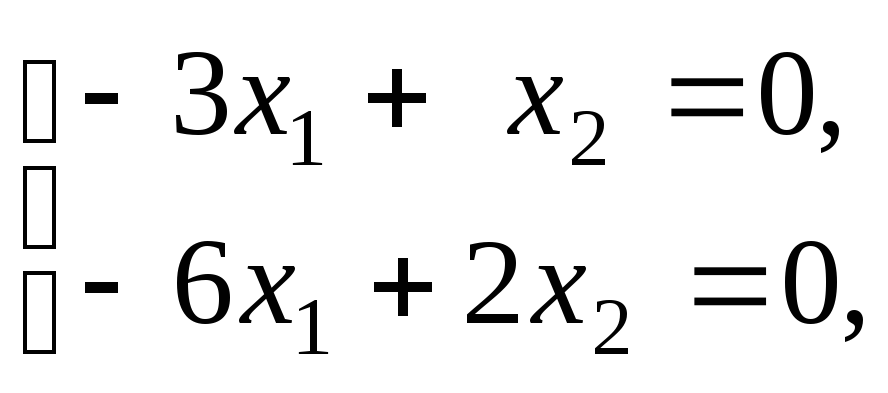 из которой находим
из которой находим Отсюда следует, что общее решение системы
имеет вид
Отсюда следует, что общее решение системы
имеет вид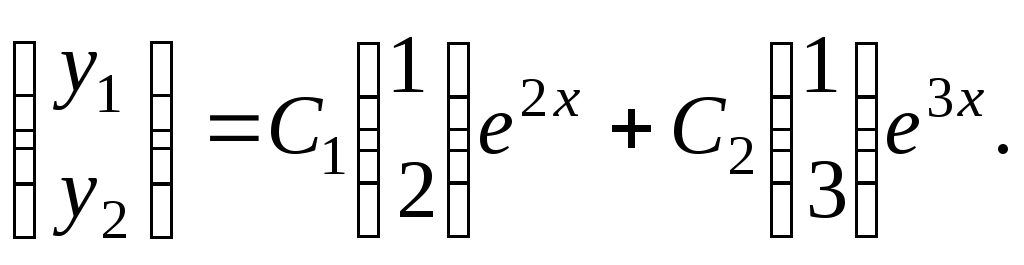 Взяв у векторов первые координаты,
получим:
Взяв у векторов первые координаты,
получим:![]() Так как
Так как![]() искомая функция, то мы получили общее
решение нашего уравнения:
искомая функция, то мы получили общее
решение нашего уравнения:![]() Формула совпадает с той, которая была
получена непосредственным решением
уравнения.
Формула совпадает с той, которая была
получена непосредственным решением
уравнения.
Решить систему
 сведя её к одному уравнению второго
порядка.
сведя её к одному уравнению второго
порядка.
Решение.
Выразим
![]() из первого уравнения:
из первого уравнения:![]() Подставим это выражение во второе
уравнение:
Подставим это выражение во второе
уравнение:![]() откуда получаем для функции
откуда получаем для функции![]() уравнение второго порядка:
уравнение второго порядка:![]() Его характеристическое уравнение имеет
корни
Его характеристическое уравнение имеет
корни![]()
![]() Следовательно,
Следовательно,![]() Теперь находим функцию
Теперь находим функцию![]()
![]()
Таким образом, общее решение системы имеет вид

Замечание.
Не всякая система дифференциальных
уравнений сводится к одному уравнению.
Примером может служить система
![]()
![]() Однако, если, например, положить
Однако, если, например, положить![]()
![]() то для функций
то для функций![]() получится уравнение второго порядка:
получится уравнение второго порядка:![]()
![]()
Решить систему методом вариации постоянных:
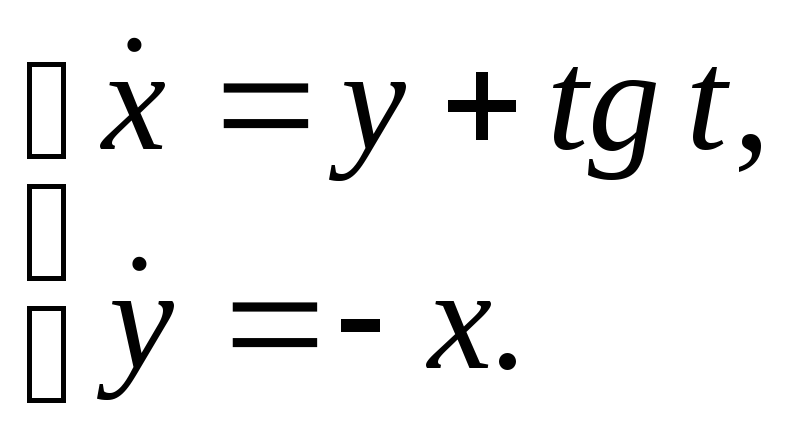
Решение.
Сначала решим однородную систему
![]() Характеристическое уравнение
Характеристическое уравнение![]() имеет корни
имеет корни![]() Собственный вектор, соответствующий
Собственный вектор, соответствующий![]() равен
равен![]() Поэтому
Поэтому![]() комплексное решение системы. Выделим
действительную и мнимую части:
комплексное решение системы. Выделим
действительную и мнимую части:
![]() Значит,
общее решение однородной системы имеет
вид
Значит,
общее решение однородной системы имеет
вид
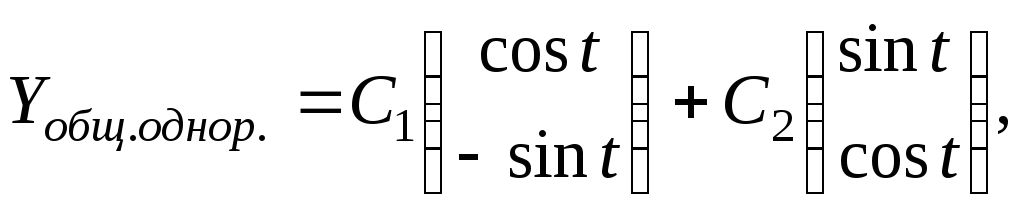 где
где![]() постоянные. Переходя к решению неоднородной
системы, будем далее считать, что
постоянные. Переходя к решению неоднородной
системы, будем далее считать, что![]()
![]() Тогда
Тогда
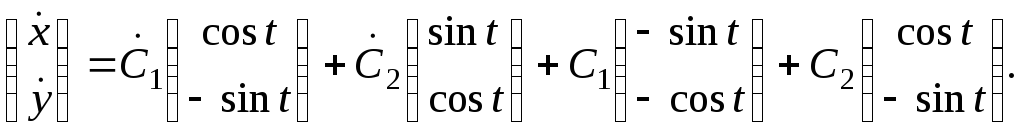
Подставив
в исходную систему, получим:
![]() Решив эту систему линейных алгебраических
уравнений относительно
Решив эту систему линейных алгебраических
уравнений относительно![]()
![]() получим:
получим:![]()
![]() Проинтегрировав эти равенства, будем
иметь
Проинтегрировав эти равенства, будем
иметь![]()
![]() где
где![]() постоянные. Таким образом, общее решение
исходной системы имеет вид
постоянные. Таким образом, общее решение
исходной системы имеет вид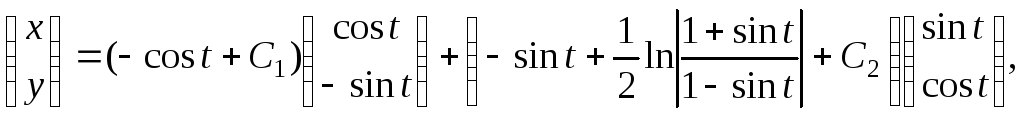 где
где![]() постоянные.
постоянные.
Задачи для самостоятельного решения
Найти все решения системы дифференциальных уравнений:
а)
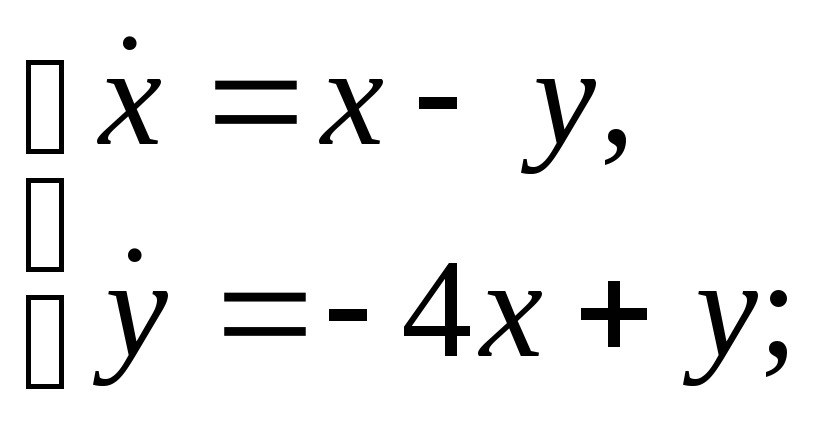 б)
б)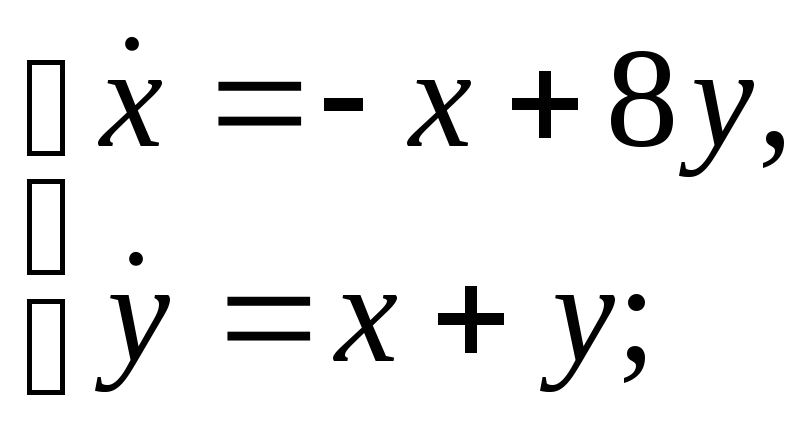 в)
в)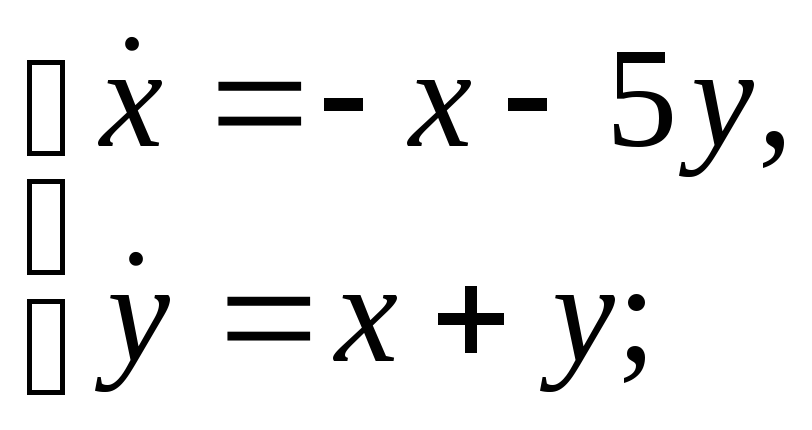 г)
г)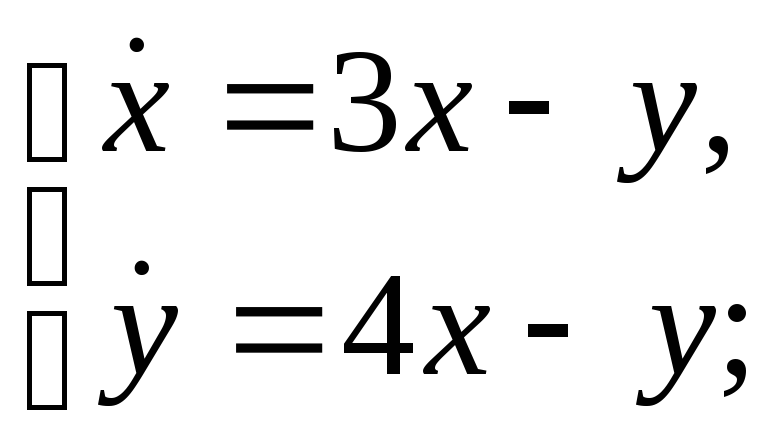
д)
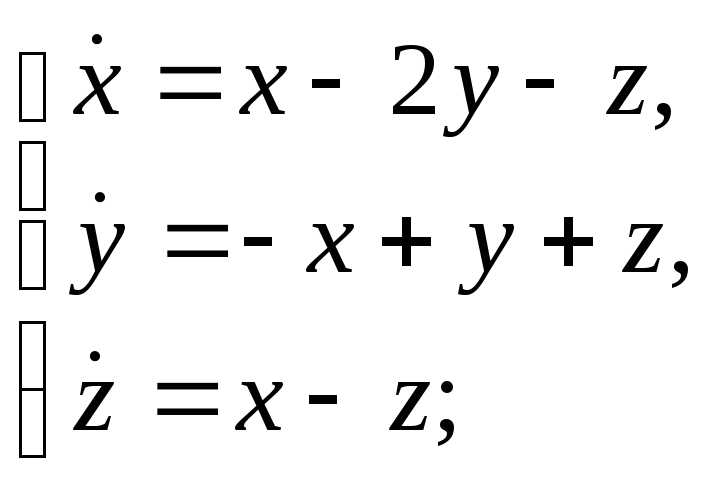 е)
е) ж)
ж)
з)
 и)
и)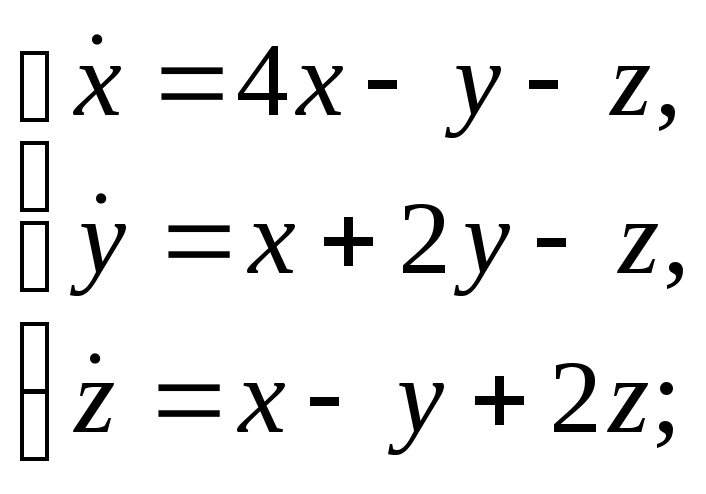 к)
к)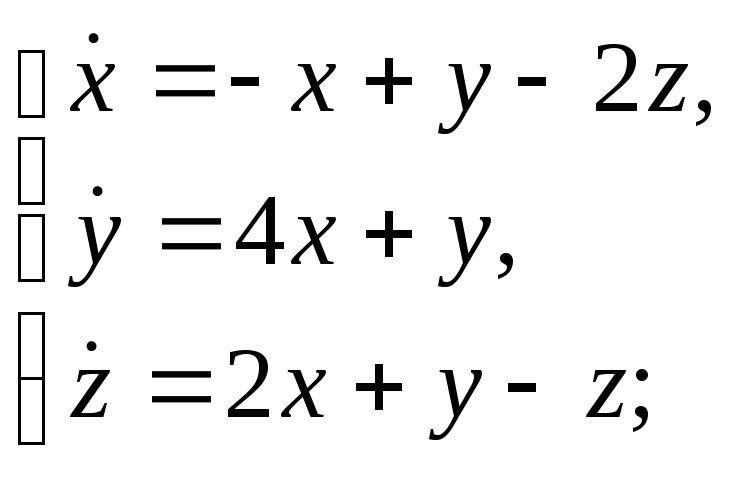
л)
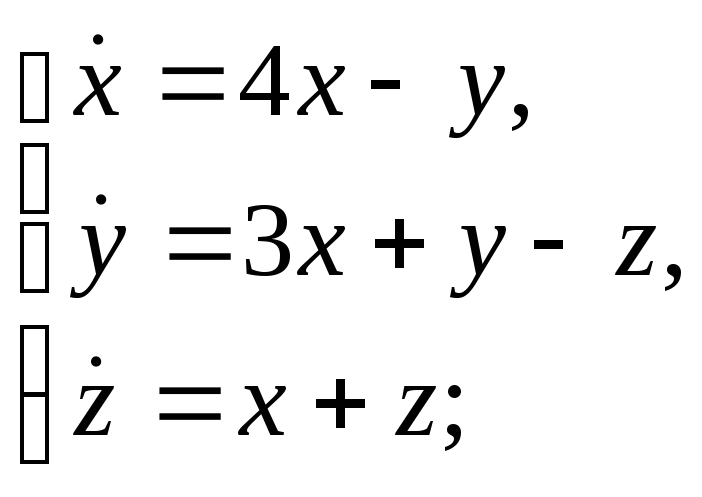 м)
м)
Решить неоднородную систему методом вариации постоянных:
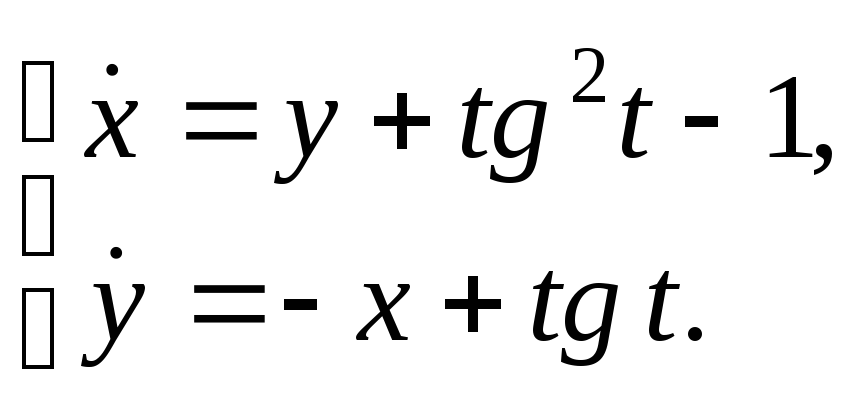
Решить систему
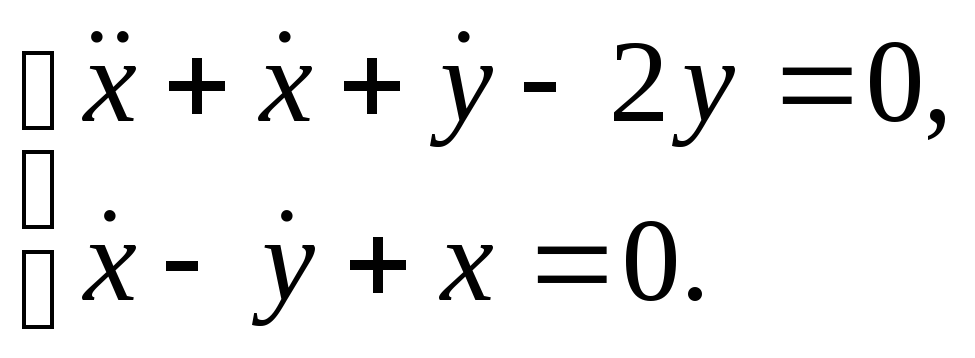
Ответы:
1. а)
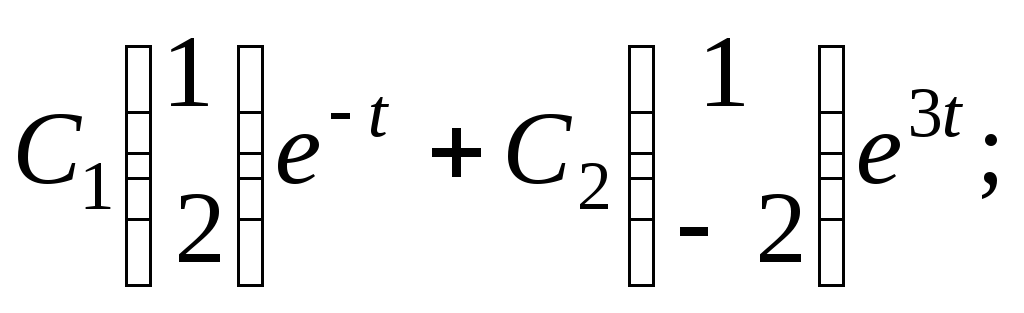 б)
б)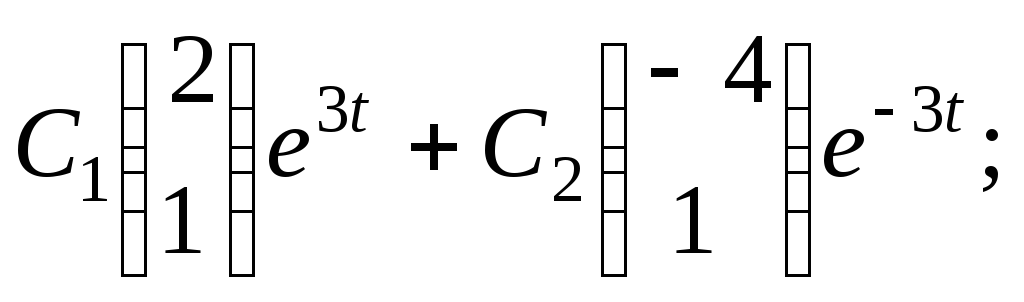
в)

г)
![]() д)
д)
е)
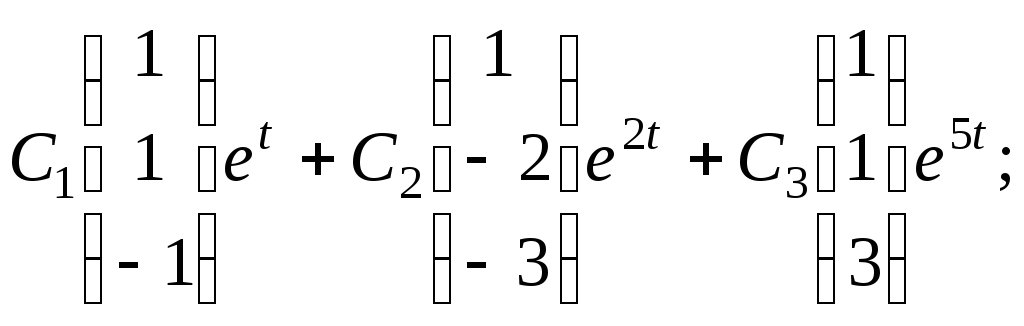
ж)
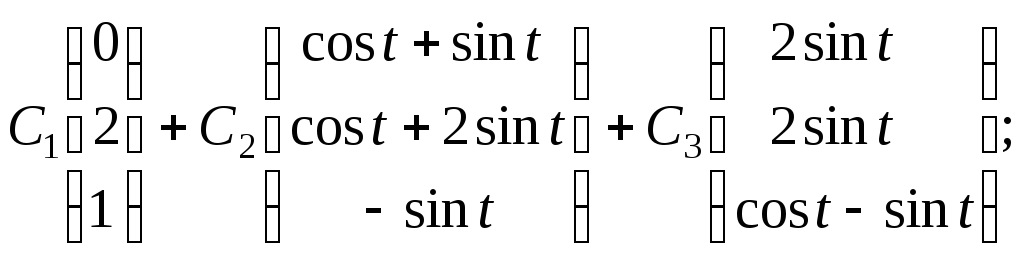
з)
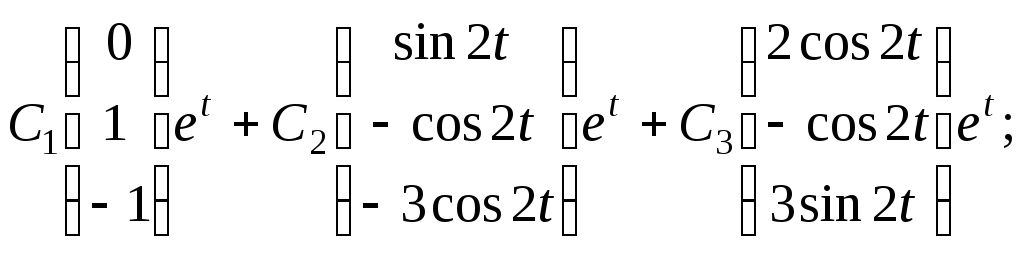
и)
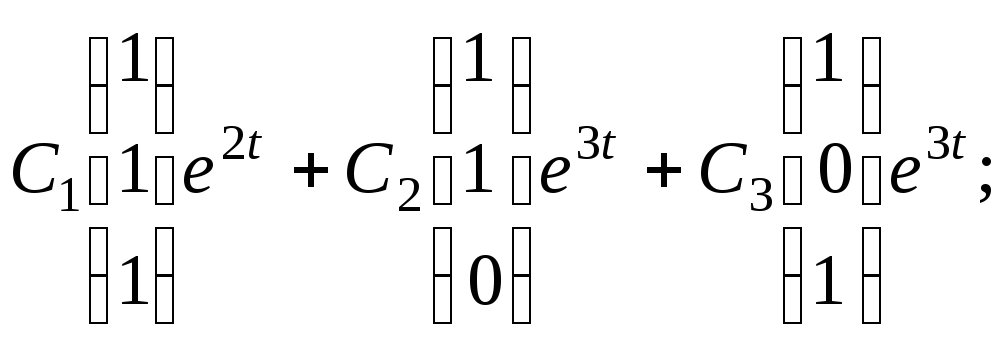 к)
к)![]()
![]()
![]()
л)
![]()
![]()
![]() м)
м)![]()
![]()
![]()
2.
![]()
![]()
