Деревья

Определение 13 (Дерево). Связный граф без циклов называется деревом.

Деревья особенно часто возникают на практике при изображении различных иерархий. Например, популярны генеологические деревья.

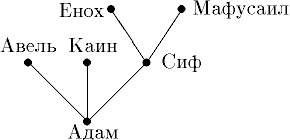
Пример 5 (генеологическое дерево). На рисунке показано библейское генеологическое дерево.

Определение 14 (Лес, листья). Граф без циклов называется лесом. Вершины

Деревья – очень удобный инструмент представления информации самого разного вида. Деревья отличаются общего случая от простых графов тем, что при обходе дерева невозможны циклы. Это делает графы очень удобной формой организации данных для различных алгоритмов. Таким образом, понятие дерева активно используется в информатике и программировании.

3 Раскраска, плоские графы Раскраска графов

Определение 15 (Раскраска). Раскраской графа G = (V,E) называется отображение : V  N . ^*

Определение 16 (Правильная раскраска). Раскраска называется правильной, если образы любых двух смежных вершин различны: (u) (v), если (u,v)  I. Хроматическим числом графа называется минимальное количество красок, необходимое для правильной раскраски графа.

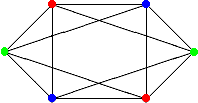
Пример 6 (раскраска). На следующем рисунке показана правильная раскраска.

Грани графа

Помимо использования в дискретной математике, графы находят применение и в непрерывной математике, особенно в топологии. При этом графы представляют геометрические объекты на некоторой поверхности (часто на плоскости или на поверхности сферы.)

Определение 17 (Плоский граф). Существует правило изображение графов на поверхности: рёбра графа должны пересекаться только своими концами, то есть в точках, представляющих вершины графа.

Для графа, который может быть изображён подобным образом на плоскости, существует название: плоский граф.

Определение 18 (Грань графа). Гранью графа, изображенного на некоторой поверхности, называется часть поверхности, ограниченная рёбрами графа.

Данное понятие грани, по-существу, совпадает с понятием грани многогранника. В качестве поверхности в этом случае выступает поверхность многогранника. Если многогранник выпуклый, его можно изобразить на плоскости, сохранив все грани. Это можно наглядно представить следующим образом: одну из граней многогранника растягиваем, а сам многогранник ``расплющиваем'' так, чтобы он весь поместился внутри этой грани. В результате получим плоский граф. Грань, которую мы растягивали ``исчезнет'', но ей будет соответствовать грань, состоящая из части плоскости, ограничивающей граф.

Таким образом, можно говорить о вершинах, рёбрах и гранях многогранника, а оперировать соответствующими понятиями для плоского графа.

Когда мы говорим ``плоский граф'', мы имеем в виду геометрический объект. Однако, конечно же не все его геометрические свойства нам важны (например, неважен абсолютный размер). Поэтому точнее считать, что плоский граф – это трёхосновная модель <V,E,S; I, B>, где V – множество вершин, E – множество рёбер, S – множество граней, I – отношение инцидентности, а B – отношение ограниченности, связывающее рёбра с ограничиваемыми ими гранями.

Теорема 2 (Обобщенная теорема Эйлера о многогранниках). Количество граней плоского графа равно его цикломатическому числу + 1.

В первоначальной формулировке теорема Эйлера о многогранниках звучала так: ``Для любого выпуклового многогранника количество вершин минус количество рёбер плюс количество граней равно 2.''

Для плоских графов существует очень знаменитая проблема четырёх красок. Она состоит в том, чтобы доказать (или опровергнуть) утверждение, что хроматическое число любого плоского графа не превосходит 4. Данная проблема была положительно решена всего несколько лет назад с использованием компьютерного анализа различных вариантов.