ТОЭ 3 часть студентам / МУ РГР Эл и магн поля

для варианта г — определить заряд трубы и провода на единицу их длины;

для варианта д — определить минимальные плотности зарядов на поверхности трубы и провода.

37. Равномерное магнитное поле, существовавшее в среде с магнитной проницаемостью μ₁= 500(рис. 29), возмущено внесенным в поле шаром, вещество которого имеет магнитную проницаемость μ₂=200. Напряженность невозмущенного поля E_о=10³А/м, радиус шара а=4см. Требуется:

для варианта а — определить напряженность магнитного поля в центре шара и в точке A(z_A=3см, Ха =4см);

для варианта б — по 5—6 точкам построить след эквипотенциальной поверхности, проходящей через точку A(z=3cm, x_A=4см);

для варианта в — по 5—6 точкам построить след эквипотенциальной поверхности, проходящей через точку В (z_B=2,71см, Хв=0),

Указание к вариантам б) и в). При построении эквипотенциали учесть, что кривая симметрична относительно оси х и поэтому все точки достаточно брать в одном квадранте.

для варианта г—определить значение магнитного потока Ф, проходящего через шар;

для варианта д — построить график H(Θ) для точек внешней поверхности шара, расположенных в плоскости рисунка.

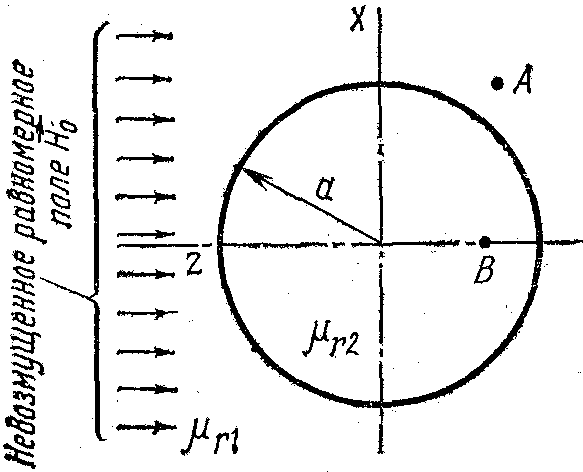
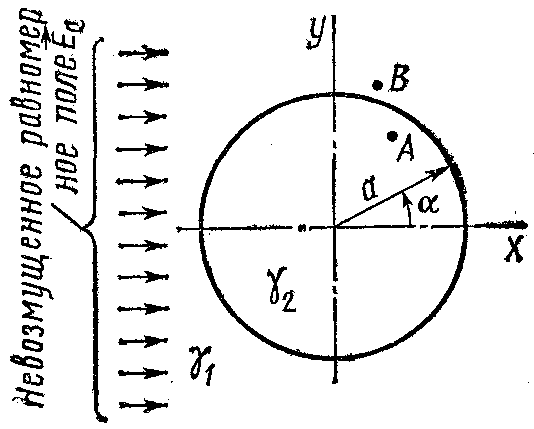
Рисунок 29. Рисунок 30.

38. Равномерное электрическое поле с напряженностью Е₀=10В/м, существующее в среде с удельной проводимостью γ₁=2•10³ 1/(Ом·м) и направленное по оси х (рис. 30), возмущено внесенным в поле цилиндром с удельной проводимостью γ₂=5•10³ 1/(Ом·м). Ось цилиндра перпендикулярна Е₀, радиус его а=8см. Требуется:

для варианта а — определить напряженность поля на оси цилиндра и в точке В (х_в=3,15см, y_в=9,5см);

для варианта б — по 5-6 точкам построить . след эквипотенциальной поверхности, проходящей через точку В (x_в=3,15см, у_в=9,5см);

для варианта в — по 5—6 точкам построить след эквипотенциальной поверхности, проходящей через точку А (x_а=4см, yа=6см).

Указание. При построении эквипотенциали учесть, что кривая симметрична относительно оси х и поэтому все точки брать в одном квадранте;

для варианта г — найти значение тока, проходящего через цилиндр на единицу его длины;

для варианта д—построить кривую зависимости плотности тока на поверхности цилиндра σ_ПОВ от угла α.

39. В существующее в воздухе (μ₁=1) равномерное магнитное поле (рис. 31) напряженностью Hо=20А/см помещен длинный ферромагнитный цилиндр радиусом а=4 см с магнитной проницаемостью μ₂=10. Ось цилиндра перпендикулярна полю. Используя аналогию между электрическим и скалярным магнитным потенциалами, составить выражения для определения скалярного магнитого потенциала в обеих средах. Определить:

для варианта а — напряженность поля H внутри ферромагнитного цилиндра в точке A с координатами Ra=2 cm, α=30°;

для варианта б — магнитный поток через сечение цилиндра В—С на длине 1 м;

для варианта в — разность скалярных магнитных потенциалов между точками D и Е;

для варианта г — магнитное напряжение φ_м между точками F и К, координаты которых R_f=5см, α_F=135°, R_k=6см, α_к=90°,

для варианта д — напряженность Н в точке F (R_f =5cm, α _F =135°).

Рисунок 31. Рисунок 32.

40. По двум медным цилиндрическим полым проводникам (рис. 32), расположенным в воздухе, проходит постоянный ток I=100А. Геометрические размеры линии r₁=1см, г₂=2см, d=5см, удельная проводимость проводов γ=5,7·10⁷1/(Ом·м). В точке A значение вектора Пойнтинга равно 1,5·10²Вт/м². Определить тангенциальную и нормальную составляющие вектора Пойнтинга в точках, расположенных непосредственно у поверхности провода:

для варианта а — в точке В; для варианта г — в точке F; для варианта б — в точке С; для варианта д — в точке К. для варианта в — в точке D.

41. По отрезку прямолинейного провода длиной 10см проходит переменный ток i=100 sin 10⁸t (А). Среда, окружающая провод — воздух. Считать, что со средней точкой отрезка провода совмещено начало отсчета сферической системы координат и что ось отсчета углов Θ совпадает с положительным направлением тока в проводе. Требуется:

1) построить полярную диаграмму зависимости от угла Θ модуля среднего за период значения вектора Пойнтинга в точках сферы радиусом R: для варианта а — R=1000 м; для варианта г — R=300м; для варианта б — R=500м; для варианта д — R=800м; для варианта в — R=100м;

2) записать выражения для мгновенных значений векторов напряженности электрического и магнитного полей в точках А и В, предварительно выяснив, в какой зоне поля находится каждая точка. Радиус R, координаты точек A и В в сферической системе координат приведены в таблице:

Вариант	RM,	ΘB˚	RM, м	ΘB˚	Вариант	RM, м	ΘB˚	RM, м	ΘB˚
а	0,5	30	500	60	Г	100	150	0,2	45
б	500	240	0,5	30	д	0,2	120	300	135
в	1	30	1000	60

42. Пространство между двумя коаксиальными круглыми цилиндрическими проводящими поверхностями заполнено средой с удельной проводимостью γ=10^-4 1/(Ом·м) и диэлектрической проницаемостью ε_г=10. Радиусы цилиндрических поверхностей r₁=3cm и г₂=5см. В точках, удаленных от оси на расстояние r=4 см, вектор плотности полного тока имеет радиальное направление, а модуль его определяется выражением δ_полн=100 sin 10⁶t (А/м²). Требуется:

1) записать выражение для мгновенного значения напряжения, подведенного к проводящим поверхностям;

2) построить график зависимости от расстояния r до оси цилиндра действующего значения:

для варианта а — плотности полного тока δ_полн=f(r);

для варианта б — напряженности электрического поля E=f(r);

для варианта в — удельных активных потерь р=f(r);

для варианта г —плотности тока проводимости δ=f(r);

для варианта д — плотности тока смещения δ_СМ=f(r).

43. Определить активное и внутреннее индуктивное сопротивления одного метра длины уединенной шины при переменном токе. Определить сопротивление 1м длины той же шины при постоянном токе и сравнить с активным сопротивлением ее при синусоидальном токе. Частота синусоидального тока f, удельная проводимость материала шины γ магнитная проницаемость материала μ и размеры поперечного сечения шины h и 2а (см. рис. 4) приведены в таблице:

Вариант	f, Гц	γ·10-7, 1/(Ом·м)	μ	h, см	2а, см
а	1500	1	1000	5	0,4
б	5000	2	600	5	0,2
в	4000	2	750	5	0,2
г	3000	0,5	6D0	5	0,6
д	2000	0,5	800	5	0,6

44. На расстоянии R от радиостанции, излучающей мощность P_s на частоте f, находится приемная прямоугольная антенна. Сферические координаты приемной антенны относительно радиостанции

R и Θ=90°. Плоскость рамки вертикальна, высота рамки а=40см, длина b, число витков w=2, высота излучателя 1м. Требуется:

1) определить действующее значение напряжения U на выводах рамочной антенны в зависимости от угла α поворота плоскости рамки; рассмотреть различные положения плоскости рамки — от перпендикулярного (α=0) направлению распространения волны до параллельного (α=90°);

2) построить зависимость U=f(α). Значения величин R, Рв, f, b приведены в таблице:

Вариант	R, км	Ps-10-8, Вт	f, МГц	b, см
а	300	1	3	5
б	430	2	3,75	4
В	520 -	3	2,5	6
Г	380	1,6	5	3
д	670	5	3,33	4,5

Указания: 1) наземная радиостанция излучает мощность в полупространство, поэтому выражение для излучаемой мощности , l – удвоенная высота реального излучателя.

2) при определении напряжения в рамке воспользоваться разностью косинусов:

.

45. Пространство между двумя плоскими дискообразными электродами диаметром 7,5см, расположенными параллельно друг другу на расстоянии 2см, заполнено средой с относительной диэлектрической проницаемостью ε и удельной проводимостью γ (величина γ не задана). К электродам подведено напряжение u=10⁴sinωt (В). Требуется:

1) определить активную проводимость между дисками, если в момент t=T/n плотности тока смещения и тока проводимости в среде между дисками одинаковы (Т—период изменения приложенного напряжения). При решении задачи краевым эффектом пренебречь. Значения ε, t₁, ω приведены в таблице:

Вариант	t1, с	ε	ω, С-1	Вариант	t1, с	ε	ω, С-1
а б в	Т/12 Т/15 Т/8	9 6,9 10,9	314 314 450	г д	Т/6 Т/10	13,5 7,9	628 450

2) определить полный ток, проходящий через конденсатор для того же момента времени.

46. Перпендикулярно направлению распространения плоской электромагнитной волны расположена массивная металлическая стенка. Незначительная доля энергии падающей волны проникает в стенку, остальная часть энергии отражается от нее. Какое расстояние пройдет волна, проникающая внутрь стенки, за то время, за которое отраженная волна в воздухе пройдет расстояние lв метров? Чему равна длина волны в воздухе и в металлической стенке?

Построить график зависимости действующего значения указанной в таблице величины от расстояния r (координата г направлена в глубь стенки), если на поверхности стенки Eо=10^-6sinωt (В/м). Значения l, частоты поля f, магнитной проницаемости μ металла и его удельной проводимости γ указаны в таблице:

Вариант	Построить график	l, м	f•10—4, Гц	μ	γ, Ом-1·м"-1
а	E(Z)	104	1	103	4
б	В(Z)	104	1	103	4
в	δ(Z)	143	70	1	57,2
г	H(Z)	5·103	2	400	5
д	H(Z)	5·103	2	400	5

47. Для двухпроводной линии переменного тока в виде двух параллельных плоских шин (см. рис. 27) частота синусоидального тока f, удельная проводимость материала шины γ, размеры поперечного сечения каждой шины h и 2а и расстояние между ними 2b приведены в таблице:

Вариант	Материал шины	γ•10—6, Ом-1 м-1	f, Гц	h, см	2а, см	2b, см
а б в г д	Латунь Медь Алюминий Медь Латунь	30 56,8 33,3 56,8 30	8000 6600 5000 11850 5800	3 1,98 2,25 2,65 2,5	0,2 0,16 0,24 0,12 0,24	0,3 0,24 0,36 0,18 0,35

Определить сопротивление 1 м длины этой линии при постоянном токе и сравнить с активным сопротивлением при переменном токе заданной частоты.

48. Плоская электромагнитная волна распространяется в проводящей среде, свойства которой определяются удельной проводимостью γ=2·10⁷ (Ом^-1·м^-1) и магнитной проницаемостью μ=1. Если выбрать систему декартовых координат так, что плоскость yOz будет параллельна фронту волны, то в точках x₁=0,8см плотность тока определяется выражением δ_x1=10⁵ sin 10⁴πt, (А/м²). Требуется:

1) записать выражение для мгновенного значения величины в точках плоскости х=0,4см:

для варианта а — напряженности электрического поля E=f(ωt);

для варианта б — напряженности магнитного поля H=f(ωt),

для варианта в — вектора Пойнтинга П=f(ωt);

для варианта г — плотности тока δ= f(ωt),

для варианта д — определить х, при котором .

2) определить длину волны и глубину проникновения волны в проводящей среде.

49. Плоская электромагнитная волна с частотой f=1000Гц распространяется в глубь толстой однородной металлической плиты с удельной проводимостью γ=5·10⁶ (Ом^-1·м^-1) и магнитной проницаемостью μ=1. Фронт волны параллелен поверхности плиты. Требуется:

1) определить напряженности электрического и магнитного полей на поверхности плиты, если поверхностный слой металла толщиной 5мм за 5мин нагревается от 20 до 520° С. Удельный вес металла 8 г/см³, его удельная теплоемкость с=0,1^-3 кал/(г·град). При решении не учитывать тепловой обмен через границы нагреваемого слоя;

2) построить график зависимости действующего значения указанной величины в функции координаты r в интервале 0<2<1см (ось z направлена от поверхности в глубь плиты): для варианта а — E=f(z); для варианта б — H=f(z); для варианта в — δ=f(z); для варианта г — П=f(z); для варианта д — B=f(z).

51. Плоская электромагнитная волна проникает из воздуха в морскую воду. Удельная проводимость морской воды γ. Фронт волны параллелен поверхности моря. На глубине 25см напряженность магнитного поля изменяется по закону H=10sin(f·6,28t) А/см.

Определить для точек на поверхности моря комплекс действующего значения указанной в таблице величины и построить график изменения ее модуля в функции расстояния от поверхности в глубь моря (z меняется от 0 до 25см):

Вариант	γ, Ом-1m-1	f·10-7, Гц	Определить	Построить график
а	1	1	Напряженность электрического поля	Е(z)
б	0,1	10	Напряженность магнитного поля	Н(z)
в	0,2	5	Плотность тока	δ(z)
г	0,5	2	Вектор Пойнтинга	П(z)
д	0,25	4	Магнитную индукцию	B(z)

52. По медной уединенной плоской шине с поперечными размерами 2а=4мм и h=4см (см. рис. 4) в направлении оси у проходит переменный ток i=160 sinωt, А. Удельная проводимость меди γ=5,6·10⁷ (Ом^-1·м^-1). Требуется:

1) определить частоту изменения тока, если известно, что напряженность электрического поля на поверхности в 1,5 раза больше, чем в средней плоскости шины;

2) построить график зависимости в функции от координаты х модуля величины:

для варианта а — напряженности электрического поля E=f(x), для варианта б — напряженности магнитного поля H=f(x), для варианта в — плотности тока δ=f(x); для варианта г — вектора Пойнтинга П=f(x); для варианта д — векторного потенциала А внутри и вне шины, приняв A=0 при х=0.

53. Две медные плоские шины толщиной 2а=1мм, высотой h=3см, расположенные на расстоянии 2b=3мм друг от друга (см. рис. 27), служат прямым и обратным проводами в цепи синусоидального тока частотой f=3000Гц. Действующее значение тока 200А. Требуется:

1) определить активную мощность, расходуемую на нагрев шин, если длина шин 5м, а удельная проводимость меди γ=5,6 10⁷ Ом^-1·м^-1;

2) построить для правой шины график зависимости в функции координаты х действующего значения величины:

для варианта а — напряженности электрического поля E=f(x),

для варианта б — плотности тока δ=f(x);

для варианта в — магнитной индукции B=f(x);

для варианта г — вектора Пойнтинга П=f(x);

для варианта д — напряженности магнитного поля H=f(x).