2.4. Гармонические колебания

Гармоническим колебанием называется такое периодическое изменение величины, которое может быть описано синусоидальным законом(Рис 2.2.):

Положительная величина А называется амплитудой гармонического колебания, (ωt+φ₀) - фазой гармонического колебания, φ₀ - начальной фазой, ω - циклической частотой:

где: f=1/Т- частота колебаний (число полных колебаний, происходящих за одну секунду). Циклическая частота измеряется в радианах в секунду (рад/с). Частота измеряется в герцах (Гц).

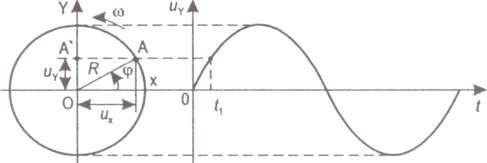
Рис. 2.2. Движение точки по окружности с постоянной скоростью

Колебания с постоянной амплитудой называются незатухающими, а колебания с непрерывно уменьшающейся амплитудой – затухающими.

2.5. Ультразвуковые волны

Звук может возникать и распространяться в средах, обладающих свойством упругости.

Упругостью называется свойство тел или выделенных объемов среды восстанавливать свою форму после прекращения действия сил, вызывающих деформацию.

Упругой средой называется такая среда, любой выделенный объем которой обладает свойством упругости.

Звуком называются колебательные движения частиц упругой среды, происходящие с частотой в пределах от 16 до 20000 Гц.

Эти частоты считаются соответственно нижним и верхним пределами слышимости звуков в воздухе человеческим ухом. Колебания с частотами ниже 16 Гц, называются инфразвуком, а свыше 20000 Гц - ультразвуком. Колебания с частотой свыше 10⁹ Гц относят к гиперзвуку.

В зависимости от упругих свойств среды в ней могут возникать упругие волны различных видов, отличающиеся направлением смещения колеблющихся частичек. В связи с этим различают:

• продольные;

• сдвиговые (или поперечные);

• поверхностные

Продольные волны

Если колебания частичек среды совпадают с направлением распространения волны, то волна называется продольной (рис. 2.3). Такая волна может быть возбуждена в твердом теле, жидкой и газообразной средах.

Рис. 2.3. Схематическое изображение продольной волны

Скорость распространения продольной волны обозначают буквой (с_l). Для некоторых материалов она равна:

• в стали – с_l – 5900м/с;

• в воде – с_l – 1450м/с;

• в воздухе – с_l – 331м/с.

Поперечные волны

Если колебания частичек среды перпендикулярны направлению распространения волны, то такая волна называется поперечной (сдвиговой) (рис. 2.4). Она может быть возбуждена только в твердом теле, которое способно упруго сопротивляться деформации сдвига.

Рис. 2.4. Схематическое изображение поперечной (сдвиговой) волны

Скорость распространения поперечной волны обозначают буквойс_t.В стали она равна с_t = 3260 м/с.

Преломление и трансформация ультразвуковых колебаний (при наклонном падении волн)

При наклонном падении продольной волны из твердом среды 1 в твердую среду 2 на границе этих двух сред происходит:

• отражение;

• преломление;

• трансформация (расщепление) волны

Если продольная упругая волна l со скоростью с_l1 падает на границу раздела двух твердых сред под углом, отличным от прямого, то отраженная и прошедшая волны преломляются и трансформируются на продольные l₁, I₂, и сдвиговые t₁, t₂ волны, распространяющиеся в первой и второй средах под различными углами (рис. 2.5).

Рис 2.5. Отражение и преломление ультразвуковых волн

При этом угол β между падающим лучом с_l, и перпендикуляром MN к поверхности раздела в точке О называется углом падения; углы β_l и β_t - углами отражения; углы α_l и α_t - углами преломления (или углами ввода соответственно продольной и сдвиговой волн).

Законы отражения и преломления упругих волн по аналогии с законами геометрической оптики формулируются так:

1. Отраженные и преломленные лучи лежат в одно плоскости с падающим лучом и нормалью к поверхности раздела сред, проведенной в точке падения.

2. Угол отражения продольной волны равен углу падения.

3. Углы падения, отражения и преломления связаны соотношением, называемым законом Снелиуса.

где с_l1, c_l2, c_t1, c_t2 - скорости распространения продольных и поперечных волн в 1 и 2 средах соотвественно.

При увеличении угла падения β продольной волны углы α_l2 и α также увеличиваются (рис. 2.6.), и при некотором значении β=β_кр1 (первый критический угол) преломленные продольные волны распространяются по поверхности, не проникая в глубь среды 2. При дальнейшем увеличении угла падения до β_кр2 (второй критичекий угол) по поверхности распространяются преломленные сдвиговые волны.

Для лучей упругих волн в полной мере справедлив закон обратимости: если луч падает из среды 1 на границу со средой 2 под углом β, преломляется и входит а среду 2 под углом α_l то луч, падающий из среды 2 на границу с первой под углом α_l после преломления войдет к среду 1 под углом β.

Рис 2.6. Иллюстрация критических углов

При угле падения β_кр1 возбуждаются продольные и поперечные волны; при втором критическом уголе β_кр2 возникает лишь поперечная волна; при β_кр3 – возбуждаются только поверхностные волны.

Расчетные критические углы составляют:

• первый критический угол β_кр1=27°;

• второй критический угол β_кр2= 56°.