
МИНИСТЕРСТВО ОБРАЗОВАНИЯ НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНО ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ
В. В. Филинов
Электроника и схемотехника.
Расчёт спектров электрических сигналов.
Учебно-методическое пособие
Москва - 2014
УДК 621.38
ББК 32.85
Рекомендовано к изданию в качестве учебно-методического пособия редакционно-издательским советом МГУПИ
Рецензент:
д.т.н. профессор Шкатов П. Н. (МГУПИ)
Филинов В.В.
Электроника и схемотехника. Расчет спектров электрических сигналов. Учебно-методическое пособие. М.: МГУПИ, 2014
Учебно-методическое пособие предназначено для студентов (бакалавров и специалистов) специальностей по радиоэлектронике и информационной безопасности, изучающих курс лекций “Электроника и схемотехника”, предназначено при подготовке к выполнению практических и расчетно-графических работ (РГР) по теме “Расчет спектров электрических сигналов”. Приведены примеры расчета спектров периодических и непериодических сигналов, а также задания для выполнения РГР. Полезно для магистров и аспирантов технических направлений МГУПИ.
Утверждено и рекомендовано решением УМС факультета «Приборостроения и радиоэлектроники» МГУПИ в качестве учебно-методического пособия.
© Московский Государственный Университет Приборостроения и Информатики, 2014
© Филинов В.В., 2014
Оглавление
Стр.
Введение. Необходимые формулы …...………………………………...4
-
Спектры амплитуд и фаз периодических сигналов ..…………6
Пример 1 ...…………………………………………………………………6
Пример 2 ……………………………………………………………...…..10
Пример 3 ……………………………………………………………...…..11
Пример 4 ……………………………………………………………...…..12
Пример 5 ……………………………………………………………...…..13
Пример 6 ……………………………………………………………...…..14
Пример 7 ……………………………………………………………...…..16
Пример 8 ……………………………………………………………...…..17
Пример 9 ……………………………………………………………...…..18
Пример 10 ………………………………………………………………...23
Пример 11 ………………………………………………………………...24
-
Спектральная плотность амплитуд и фаз периодических сигналов ……..….…………..………………………..…….……………...27
Пример 12 …………………………..……………………….……………27
Пример 13 …………………………..……………………….……………29
Пример 14 …………………………..……………………….……………31
Пример 15 …………………………..……………………….……………31
Пример 16 …………………………..……………………….……………33
Пример 17 …………………………..……………………….……………34
Пример 18 …………………………..……………………….……………36
Пример 19 …………………………..……………………….……………37
-
Литература ……………………………………………………………....39
-
Задания для расчетно-географических работ…………..……...39
Необходимые формулы.
Применительно
к периодическому гармоническому
напряжению
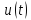 можно использовать разложение в ряд
Фурье:
можно использовать разложение в ряд
Фурье:
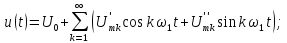
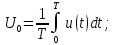 (1)
(1)
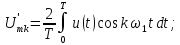
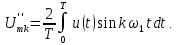
Простейшим периодическим сигналом является гармоническое колебание вида
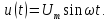
Разложение последовательности прямоугольных импульсов рис. 1.1 имеет вид:
 (2)
(2)
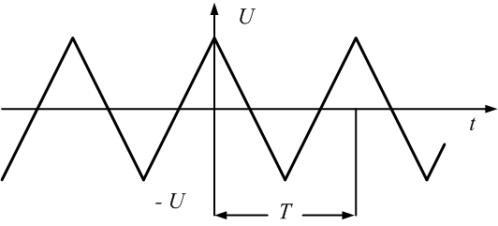
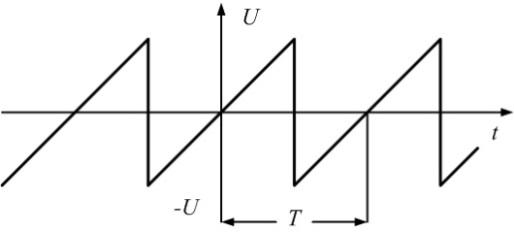
Разложение последовательности пилообразных импульсов рис. 1.2 имеет вид:
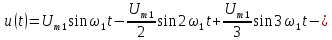
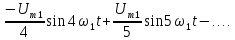 (3)
(3)
Две равнозначные записи ряда Фурье:
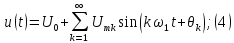
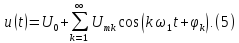
Ряд Фурье в комплексной форме:
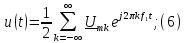
Выражение для комплексного спектра сигнала:
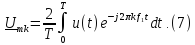
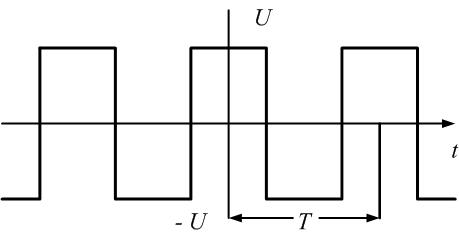
Ряд Фурье периодической последовательности прямоугольных импульсов амплитудой U (рис. 1.5а) имеет вид:
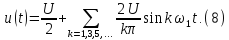
Напряжение на участках цепи находят, используя принцип суперпозиции, например напряжение на резисторах:

Расчет
цепи от отдельных постоянной и
гармонических составляющих напряжения
проводится в символической форме. При
этом нужно иметь в виду, что на k-й
гармонике сопротивление индуктивности
 ,
а сопротивление емкости
,
а сопротивление емкости
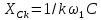 .
.
Интеграл Фурье:
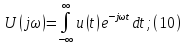
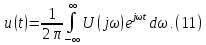
Уравнения (10) и (11) являются основными в теории спектров непериодических сигналов, причем (10) называется прямым, а (11) – обратным преобразованием Фурье (интегралом Фурье).
Комплексная придаточная функция по напряжению:
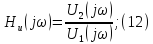
Из выражений:
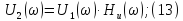
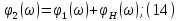
следует,
что спектральная плотность амплитуд
 реакции цепи равна произведению
спектральной плотности амплитуд
реакции цепи равна произведению
спектральной плотности амплитуд
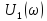 воздействия АЧХ
воздействия АЧХ
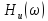 цепи, а спектральная плотность фаз
цепи, а спектральная плотность фаз
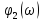 реакции цепи равна сумме спектральной
плотности фаз
реакции цепи равна сумме спектральной
плотности фаз
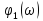 воздействия и ФЧХ
воздействия и ФЧХ
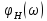 цепи.
цепи.
-
Спектры амплитуд и фаз периодических сигналов.
Пример 1. Определим параметры синусоид, формирующих последовательности прямоугольных (рис. 1.1, а) и пилообразных (рис. 1.2, а) импульсов, имеющих амплитуду U = 10 В и период Т = 20 мс.
а) Для формирования периодической последовательности прямоугольных импульсов амплитуда основной синусоиды должна быть
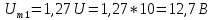 .
.
Частота колебаний этой синусоиды обратно пропорциональна периоду:
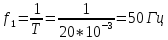 .
.
Круговая
частота
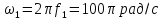 .
Таким образом, основная синусоида
.
Таким образом, основная синусоида
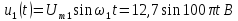 .
.
Все последующие синусоиды в соответствии с (2) должны иметь амплитуды в нечетное количество раз меньшие, а частоты - в это же нечетное количество раз большие, чем у основной синусоиды:
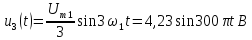 ;
;
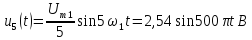 ;
;

и т.д.
Последовательность прямоугольных импульсов, изображенных на рис. 1.1, а, - это сумма синусоид:
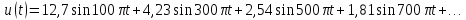 .
.
Сигнал
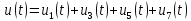 изображен
на рис. 1.1, д.
изображен
на рис. 1.1, д.
6) Для формирования последовательности пилообразных импульсов необходимо, чтобы амплитуда основной синусоиды была, как мы уже знаем [1, 3], равна

Частота основной синусоиды
 ,
,

Таким образом,
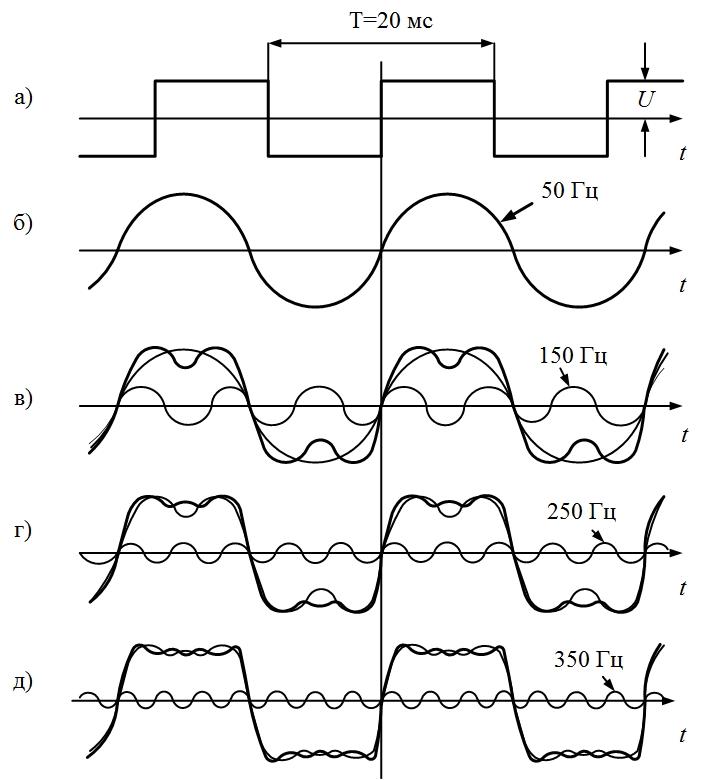
Рис. 1.1. Последовательность прямоугольных импульсов и образующие ее синусоиды
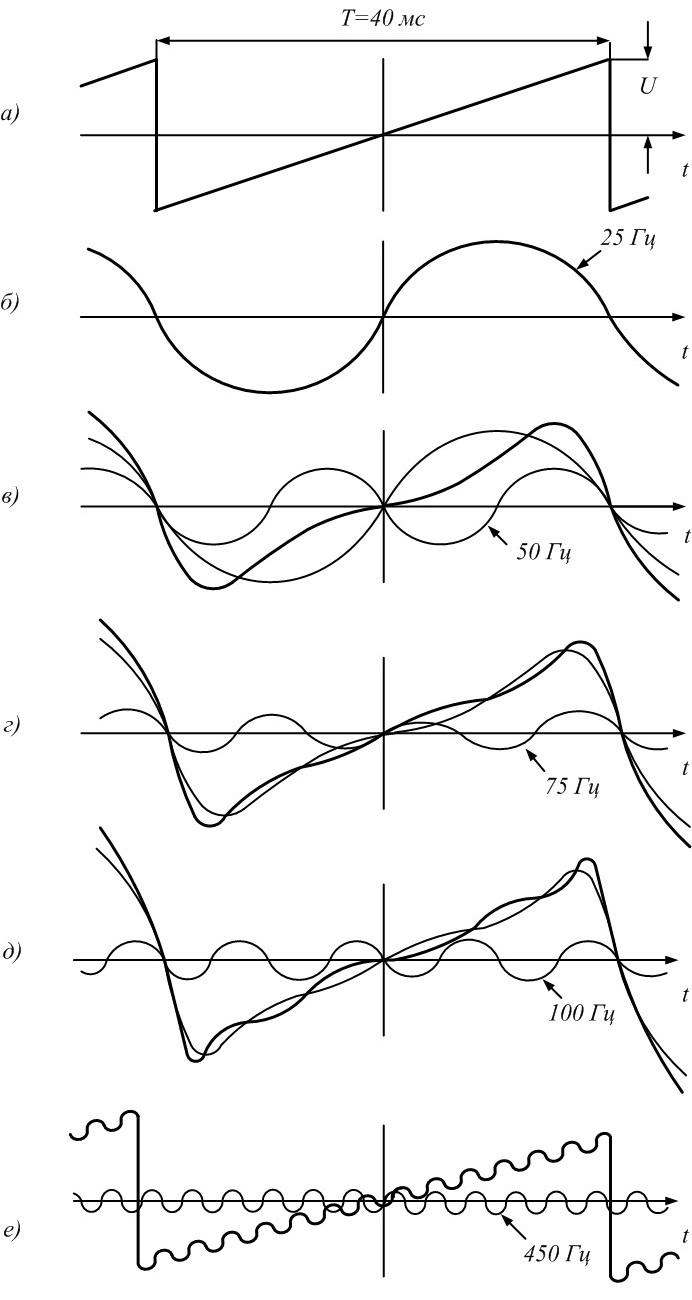
Рис. 1.2. Последовательность пилообразных импульсов и образующие ее синусоиды
Таблица 1.1. Ряды Фурье наиболее часто встречающихся сигналов
|
Сигнал |
Ряд Фурье |
|
|
|
|
|
|
|
|
|
|
|
k-четные;
|
|
|
k-четные;
|
|
|
|
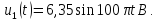
Последующие синусоиды в соответствии с (3) будут иметь вид
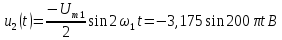

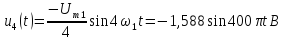
и т.д.
Последовательность пилообразных импульсов - это сумма синусоид:
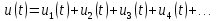 .
.
Чем больше синусоид используется при формировании сигнала, тем ближе его форма к пилообразной (рис. 1.е).
Пример 2. Определим гармонический состав последовательности треугольных импульсов, изображенных на рис. 1.3, имеющих амплитуду, U = 10 B и период Т = 10 мс.
Периодический сигнал на рис. 1.3 отличается от сигнала во второй строке табл. 1.1 на величину постоянной составляющей
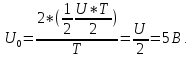
Частота основной составляющей сигнала
 или
или
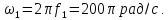
Амплитуда основной составляющей сигнала рассчитывается по формуле, приведенной в табл. 1.1, или по одной из формул (1):
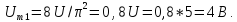
Четная функция (рис. 1.3) содержит только косинусоиды, амплитуды и частоты которых определяются по формулам, приведенным во второй строке табл. 1.1.
Амплитуда и частота третьей гармоники:
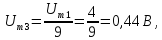
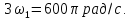
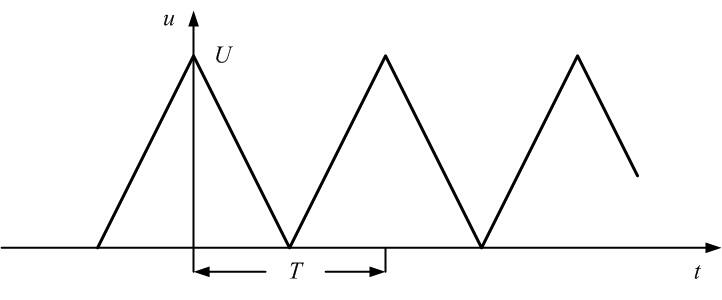
Рис. 1.3. Последовательность треугольных импульсов
Амплитуда и частота пятой гармоники:

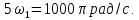
Амплитуда и частота седьмой гармоники:


и т.д.
Гармонический состав последовательности треугольных импульсов (рис.1.3) имеет вид:
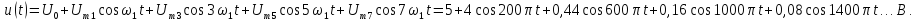
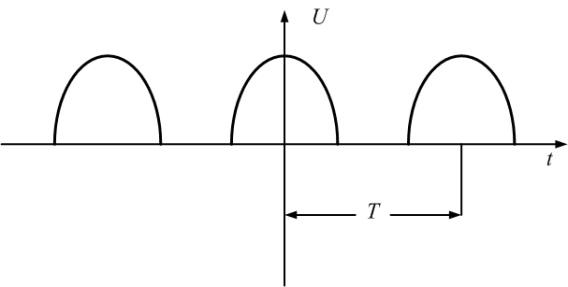
Пример 3. Представим переменное напряжение, выпрямленное двухполупериодным выпрямителем (пятая строка табл. 1.1), рядом Фурье в тригонометрической форме (5).
Из табл. 1.1 следует, что переменное напряжение u(t) представлено рядом Фурье:
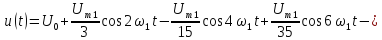
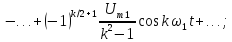
k – четные.
Постоянная
составляющая напряжения u(
t)
рассчитывается по формуле
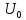 =
0,635U.
=
0,635U.
Нечетные гармоники отсутствуют в ряде Фурье, поскольку функция u( t)- четная.
Для
расчета амплитуд четных гармоник
нео6ходимо определить
 =
1,27U.
Тогда амплитуда второй гармоники
=
1,27U.
Тогда амплитуда второй гармоники
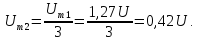
Начальная
фаза второй гармоники равна нулю:

Амплитуда четвертной гармоники
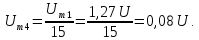
Фаза
четвертой гармоники
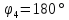 , так как в ряде Фурье перед слагаемым
, так как в ряде Фурье перед слагаемым
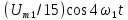 стоит знак «минус».
стоит знак «минус».
Амплитуда шестой гармоники
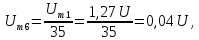
а ее фаза, а также фазы десятой, четырнадцатой и т.д. гармоник равны нулю.
Амплитуда восьмой гармоники

а ее начальная фаза, так же как и фазы гармоник с номерами 12, 16, 20 и т.д., равна 180˚.
Тригонометрическая форма ряда Фурье рассматриваемого напряжения имеет вид:
 .
.
Пример 4. Представим ряд Фурье, полученный в примере 3, в комплексной форме, ограничив его восьмой гармоникой.
В соответствии с (6) значения постоянной составляющей и амплитуд гармоник уменьшаются в 2 раза по сравнению со значениями, которые 6ыли рассчитаны в примере 3. Поэтому ряд Фурье в комплексной форме имеет вид
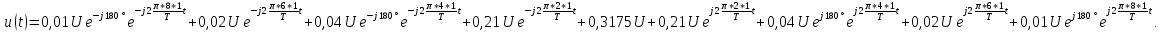
Пример 5. Построим спектр амплитуд и фаз выпрямленного напряжения
(строка 5 табл, 1.1), имеющего амплитуду U = 10 В и период Т = 10 мс.
При решении примера 3 была получена тригонометрическая форма ряда Фурье, соответствующая выпрямленному напряжению:
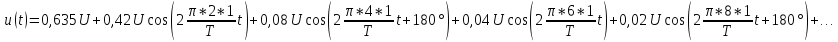 .
.
Частота основной составляющей сигнала определяется периодом колебаний:
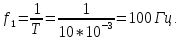
В
спектре сигнала отсутствуют нечетные
гармоники, так как само колебание
является четной функцией. Частоты высших
гармоник с четными номерами кратны этим
номерам: частота второй гармоники равна
2 = 200 Гц, четвертой, шестой, восьмой гармоник
- 400, 600, 800 Гц соответственно и т.д.
= 200 Гц, четвертой, шестой, восьмой гармоник
- 400, 600, 800 Гц соответственно и т.д.
Постоянная составляющая
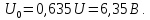
Амплитуды четных гармоник спектра в соответствии с выражениями, полученными для ряда Фурье, имеют следующие значения:
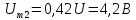 ;
;
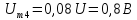 ;
;
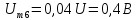 ;
;
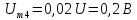
и т.д.
Фазы гармоник поочередно принимают значения 0 и 180˚.

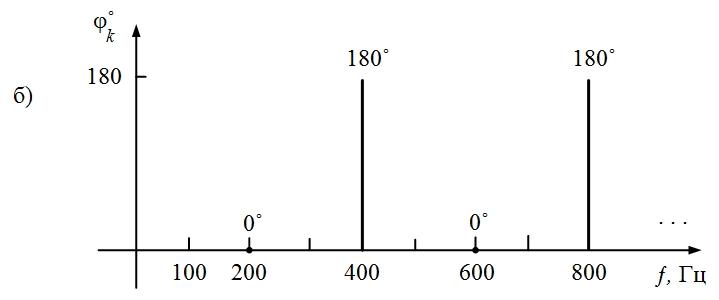
Рис. 1.4. Спектры амплитуд и фаз выпрямленного напряжения
Пример 6. Рассмотрим периодическую последовательность прямоугольных импульсов, показанную на рис. 1.5, а:
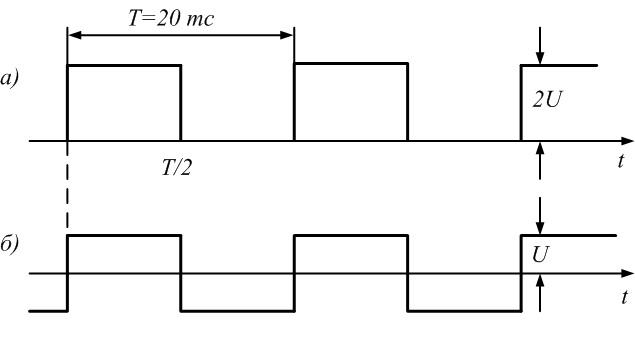
Рис. 1.5. Последовательности прямоугольных импульсов
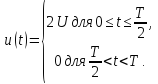
Она
имеет постоянную составляющую, равную
в соответствии с (1)
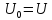 .
Коэффициенты
.
Коэффициенты
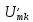 вычисляются
по формуле (1):
вычисляются
по формуле (1):
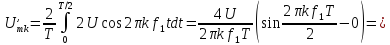

Здесь
6ыло учтено, что
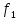 =
1/Т.
=
1/Т.
Коэффициенты
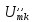 вычисляются по формуле (1):
вычисляются по формуле (1):
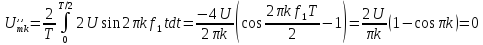
Выражение
 удовлетворяет соотношению
удовлетворяет соотношению
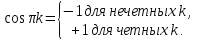
Поэтому
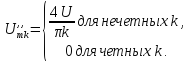
Форма ряда Фурье будет содержать только синусоиды с нечетными гармоническими частотами:

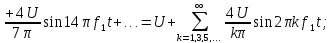
что, естественно, с точностью до постоянной составляющей U совпадает с полученным ранее выражением (2).
Переход к форме ряда Фурье (5) дает
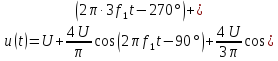
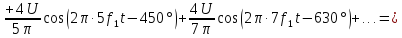

Спектр такого сигнала без постоянной составляющей показан на рис. 1.6:
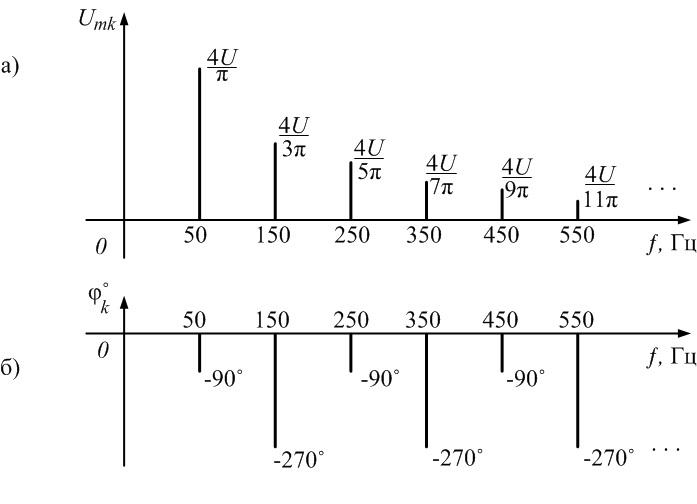
Рис. 1.6. Спектры амплитуд и фаз сигнала рис. 1.5а
Пример
7.
Представим спектр сигнала
 из примера 6 в комплексной форме.
из примера 6 в комплексной форме.
Комплексный спектр периодической последовательности прямоугольных импульсов рассчитывается по формуле (7):
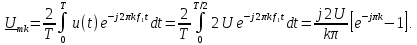
Функция
 имеет значения
имеет значения

Это
значит, что комплексный спектр
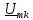 существует только для нечетных гармоник:
существует только для нечетных гармоник:
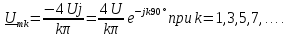
Заметим,
что в спектре
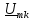 нет постоянной составляющей
нет постоянной составляющей
 ,
которая рассчитывается по формуле (1) и
равна U.
,
которая рассчитывается по формуле (1) и
равна U.
Полученный
комплексный спектр
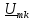 соответствует спектрам амплитуд и фаз,
изображенным на рис. 1.6.
соответствует спектрам амплитуд и фаз,
изображенным на рис. 1.6.
Пример 8. Найдем спектр последовательности прямоугольных импульсов, изображенных на рис. 1.7.
Сигнал, изображенный на рис. 1.7, имеет следующие параметры: амплитуда U = 10 В, длительность импульса τ= 10 мс, период повторения импульсов Т = 40 мс, скважность q = Т/τ = 4. Спектр этого сигнала в форме (Табл. 1.1, строка 6) имеет вид
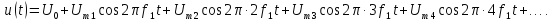
Постоянная составляющая
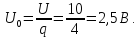
Частота первой гармоники
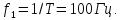
Частоты высших гармоник кратны 100 Гц. Амплитуды первых шести гармоник, рассчитываемые по формуле (3.28)
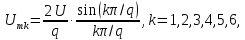
имеют следующие значения:

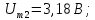
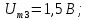
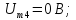
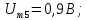
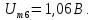
Фазы
первой, второй, третьей гармоник равны
0˚, фазы пятой и шестой гармоник равны
180˚, так как при расчете
 и
и
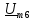 получены отрицательные значения.
Амплитуды и фазы последующих гармоник
рассчитывают аналогичным образом.
Причем, амплитуды гармоник, кратных
скважности q, т.е. четвертой, восьмой,
двенадцатой, шестнадцатой гармоник и
т.д., равны нулю. Спектры амплитуд и фаз
сигнала, изображенного на рис. 1.7,
приведены на рис. 1.8.
получены отрицательные значения.
Амплитуды и фазы последующих гармоник
рассчитывают аналогичным образом.
Причем, амплитуды гармоник, кратных
скважности q, т.е. четвертой, восьмой,
двенадцатой, шестнадцатой гармоник и
т.д., равны нулю. Спектры амплитуд и фаз
сигнала, изображенного на рис. 1.7,
приведены на рис. 1.8.
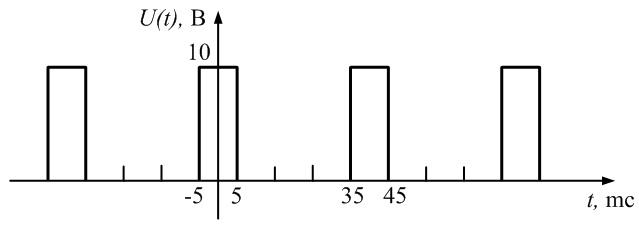
Рис. 1.7. Последовательность прямоугольных импульсов со скважностью q = 4
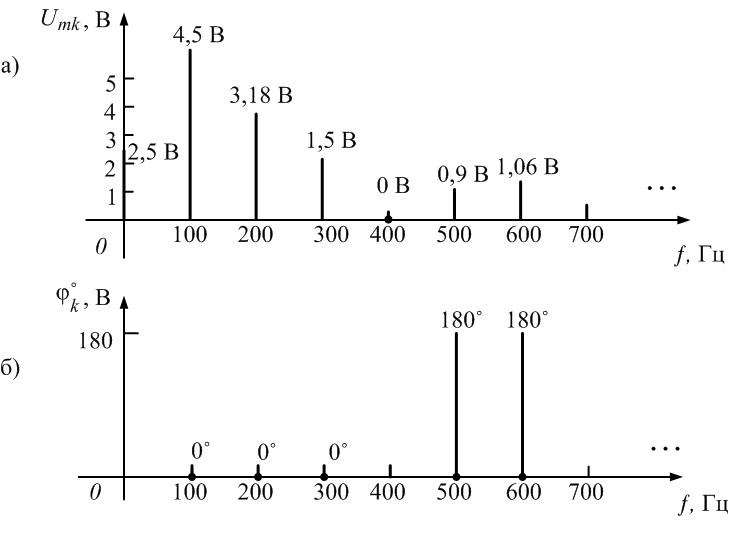
Рис. 1.8. Спектр последовательности прямоугольных импульсов со скважностью q = 4
Пример
9.
Определим напряжение на резисторе
 в
последовательном колебательном контуре,
на который подается последовательность
прямоугольных импульсов (рис. 1.10).
Параметры элементов контура и сигнала
заданы: R = 2 Ом; L = 0,704 мГн; С = 4 мкФ; U = 5
В; Т = 1 мс; τ = 0,5 мс.
в
последовательном колебательном контуре,
на который подается последовательность
прямоугольных импульсов (рис. 1.10).
Параметры элементов контура и сигнала
заданы: R = 2 Ом; L = 0,704 мГн; С = 4 мкФ; U = 5
В; Т = 1 мс; τ = 0,5 мс.
Найдем параметры постоянной и гармонических составляющих сигнала (рис. 1.10), представленного рядом Фурье (8). Частота первой гармоники
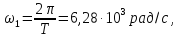 или
или
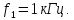
Частоты
третьей, пятой и т.д. гармоник равны
соответственно: 3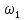 = 18,84 рад/с; 3
= 18,84 рад/с; 3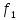 = 3 кГц; 5
= 3 кГц; 5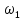 = 31,4 рад/с; 5
= 31,4 рад/с; 5 = 5 кГц; … .
= 5 кГц; … .


Амплитуды четных гармоник равны нулю. Амплитуды нечетных гармоник рассчитываются по формуле (1):

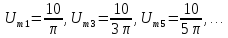 .
.
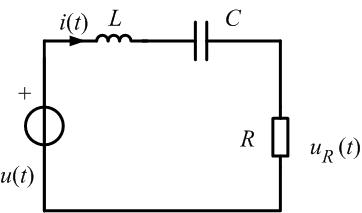
Ряд Фурье сигнала имеет вид:
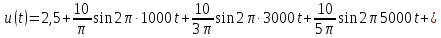
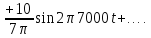
Рис. 1.9. Последовательный колебательный контур с источником периодического сигнала
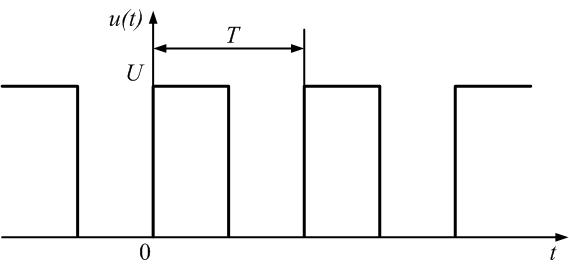
Рис. 1. 10. Последовательность прямоугольных импульсов
Определим
резонансную частоту
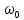 и
и
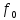 контура
(рис. 1.9):
контура
(рис. 1.9):
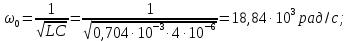
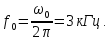
Резонанс в контуре наступает на частоте третьей гармоники входного напряжения.
Добротность контура
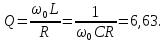
Определим гармонические составляющие тока в цепи и напряжения на резисторе в каждой из составляющих ряда Фурье схем, изображенных на рис. 1.9.
Схема
последовательного колебательного
контура с источником постоянного
напряжения
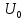 =
=
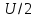 = 2,5 В приведена на рис. 1.11. В этой цепи
сопротивление индуктивности равно
нулю, а сопротивление конденсатора
равно бесконечности, поэтому
= 2,5 В приведена на рис. 1.11. В этой цепи
сопротивление индуктивности равно
нулю, а сопротивление конденсатора
равно бесконечности, поэтому
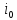 = 0;
= 0;
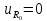 .
.
В цепи, изображенной на рис. 1.12, в контур включен источник напряжения, соответствующий напряжению первой гармоники. Синусоидальное напряжение
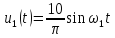
заменено
на комплексное
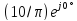 .
На частоте
.
На частоте
 = 1 кГц (
= 1 кГц (
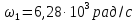 )
сопротивление индуктивности
)
сопротивление индуктивности
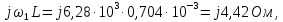
а сопротивление емкости

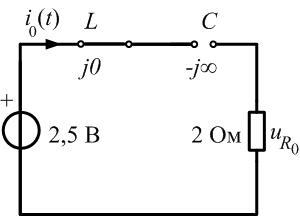
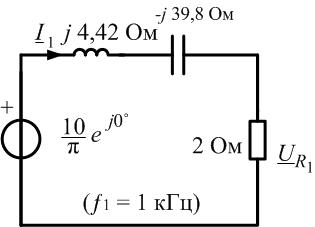
Рис. 1.11. Контур с источником постоянного напряжения
Рис. 1.12. Контур с источником напряжения первой гармоники
Комплексное сопротивление цепи
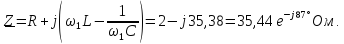
Определим
комплексные значения тока
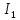 и напряжение
и напряжение
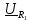 :
:
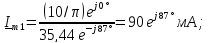

Это соответствует составляющей синусоидального напряжения (9) в исходной цепи:
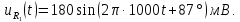
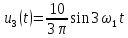
На
третьей гармонике синусоидальный
источник заменяется источником
комплексного напряжения
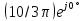 .
В результате имеем цепь, изображенную
на рис. 1.13.
.
В результате имеем цепь, изображенную
на рис. 1.13.
На
частоте
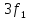 = 3 кГц (
= 3 кГц (
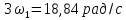 )
в цепи наступает резонанс напряжений.
Сопротивления индуктивности и емкости
равны по величине и противоположны по
знаку:
)
в цепи наступает резонанс напряжений.
Сопротивления индуктивности и емкости
равны по величине и противоположны по
знаку:
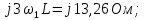

Комплексное
сопротивление цепи
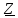 = R = 2 Ом. Ток
= R = 2 Ом. Ток

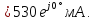
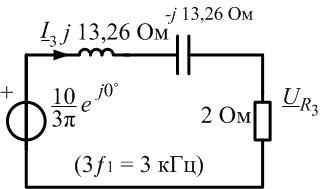

Рис. 1.13. Контур с источником третьей гармоники
Рис. 1.14. Контур с источником напряжения пятой гармоники
Напряжение
на резисторе
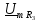 равно входному напряжению:
равно входному напряжению:
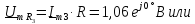
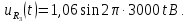
 На
пятой гармонике синусоидальный источник
На
пятой гармонике синусоидальный источник
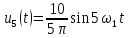
заменяется
источником комплексного напряжения
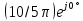 (рис. 1.14). На частоте
(рис. 1.14). На частоте
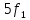 = 5 кГц (
= 5 кГц (
 )
сопротивления индуктивности и емкости
равны соответственно
)
сопротивления индуктивности и емкости
равны соответственно
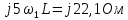 и
и
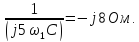
Комплексное сопротивление цепи
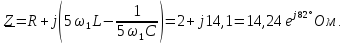
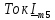 рассчитаем
по формуле:
рассчитаем
по формуле:
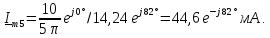
Напряжение на резисторе
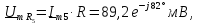
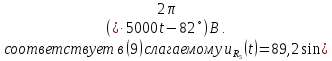
Таким
образом, ряд Фурье напряжения на резисторе
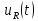 имеет вид,
имеет вид,
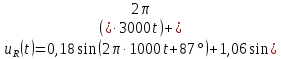

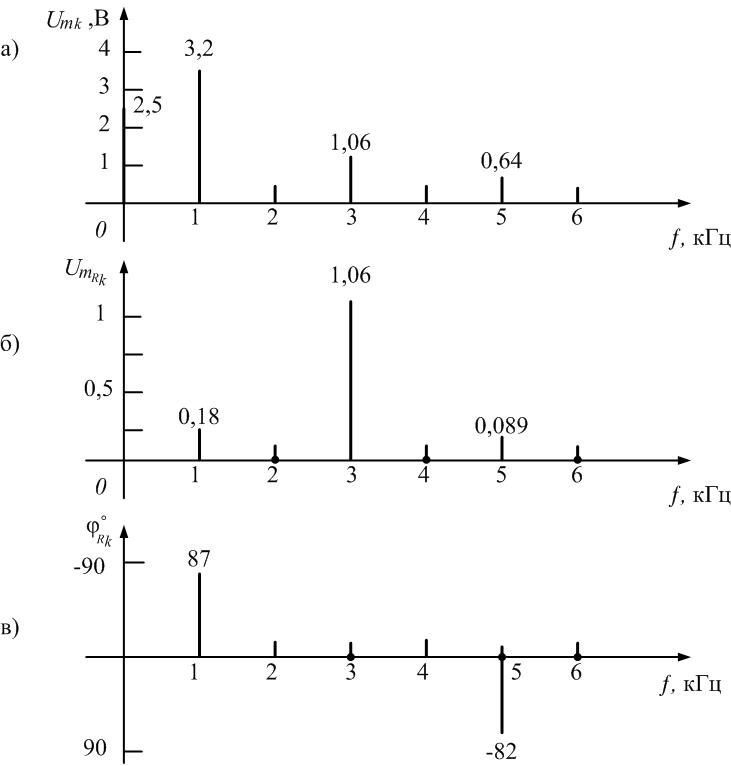
Рис. 1.15. Спектры амплитуд и фаз входного напряжения и напряжения на резисторе в колебательном контуре
Спектры
амплитуд и фаз этого напряжения изображены
на рис. 1.15
( 6, в).
Анализ спектра
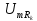 показывает, что колебательный контур
выделил третью гармонику из входной
последовательности и подавил остальные
гармоники, т.е. явление резонанса можно
использовать для, выделения отдельных
гармоник из периодического несинусоидального
сигнала.
показывает, что колебательный контур
выделил третью гармонику из входной
последовательности и подавил остальные
гармоники, т.е. явление резонанса можно
использовать для, выделения отдельных
гармоник из периодического несинусоидального
сигнала.
Пример
10.
Сравним спектры амплитуд (рис. 1.15) входной
последовательности прямоугольных
импульсов
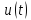 и напряжения
и напряжения
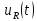 на резисторе колебательного контура
из примера 9, чтобы определить коэффициенты
передачи по напряжению цепи на частотах
гармоник.
на резисторе колебательного контура
из примера 9, чтобы определить коэффициенты
передачи по напряжению цепи на частотах
гармоник.
В
соответствии с формулой и рис. 1.15 (а),
постоянная составляющая
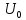 в спектре напряжения
в спектре напряжения
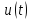 равна 2,5 В. Амплитуды первой, третьей и
пятой гармоник имеют значения:
равна 2,5 В. Амплитуды первой, третьей и
пятой гармоник имеют значения:
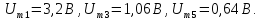
Постоянная
составляющая в спектре напряжения
 на резисторе (рис. 3.15, б)
равна нулю, а амплитуды нечетных гармоник
равны соответственно
на резисторе (рис. 3.15, б)
равна нулю, а амплитуды нечетных гармоник
равны соответственно
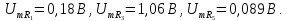
Коэффициенты
передачи по напряжению
 на частотах гармоник рассчитаем по
формуле
на частотах гармоник рассчитаем по
формуле
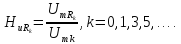
На
частоте f
= 0 кГц получаем
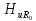 = 0/2,5 = 0. На частоте f
= 1 кГц (частота основной составляющей)
= 0/2,5 = 0. На частоте f
= 1 кГц (частота основной составляющей)
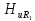 = 0,18/3,2 = 0,056.
= 0,18/3,2 = 0,056.
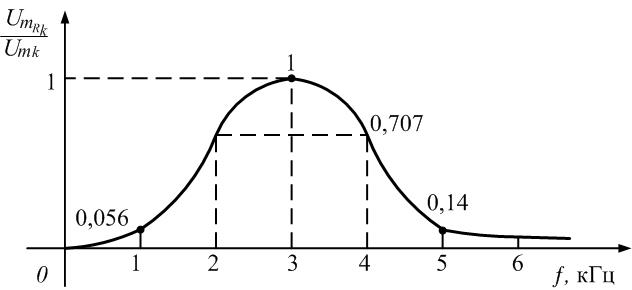
Рис. 1.16. Коэффициенты передачи по напряжению на резисторе R на частотах гармоник
На
частоте
f=3
кГц (третья гармоника)
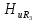 = 1,06/1,06 = 1.
= 1,06/1,06 = 1.
На
частоте f=
5 кГц (пятая гармоника)
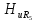 = 0,089/0,64= 0,14.
= 0,089/0,64= 0,14.
На рис. 1.16 приведен график зависимости коэффициента передачи контура от частоты гармоник. На частоте резонанса коэффициент передачи максимален и равен 1. На частотах первой и пятой гармоник коэффициент передачи резко уменьшается.
Пример 11. Определим спектр амплитуд напряжения на резисторе в цепи, изображенной на рис. 1.17, а, на вход которой поступает периодическая последовательность прямоугольных импульсов (рис. 1.17, б), если заданы R = 50 Ом, L = 10 мГн, U = 10 В, τ = 1 мс, Т = 4 мс.
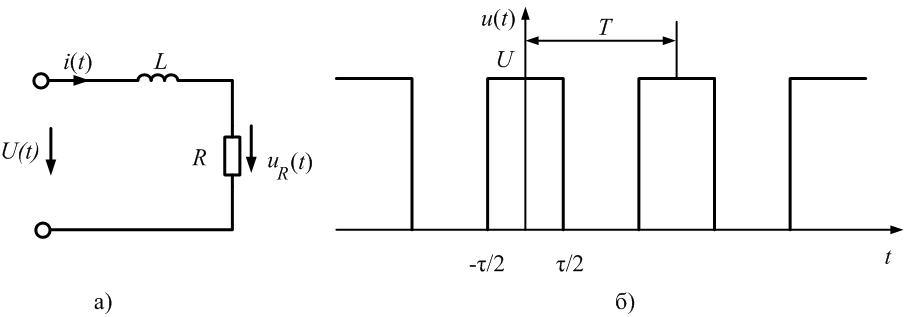
Рис. 1.17. RL-цепь и сигнал на ее входе
Найдем комплексный спектр входного сигнала u(t), воспользовавшись (7):
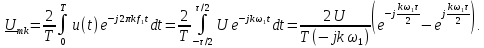
Применив формулу Эйлера, получим
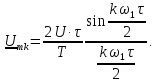
Вычислим амплитуды спектральных составляющих
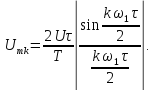
Амплитуда постоянной составляющей
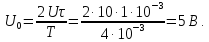
Частота основной составляющей

а ее амплитуда

Аналогичным образом определяются частоты и амплитуды высших гармоник:
|
При |
k=2
|
2
|
|
|||
|
|
k=3
|
3
|
|
|||
|
|
k=4
|
4
|
|
|||
|
|
k=5
|
5
|
|
|||
|
|
k=6
|
6
|
|
|||
|
|
k=7
|
7
|
|
|||
|
|
k=8
|
8
|
|
|||
|
|
k=9
|
9
|
|
|||
|
|
k=10
|
10
|
|
|||
Спектр
амплитуд
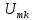 входного сигнала изображен на рис.
1.18, а.
Огибающая спектра амплитуд прямоугольных
импульсов изменяется по закону
входного сигнала изображен на рис.
1.18, а.
Огибающая спектра амплитуд прямоугольных
импульсов изменяется по закону
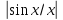 ,
нули спектра расположены на частотах,
кратных
,
нули спектра расположены на частотах,
кратных
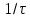 =1 кГц (четвертая, восьмая, двенадцатая
и т.д. гармоники). Комплексная передаточная
функция цепи (рис. 1.17, а) определяется
по формуле
=1 кГц (четвертая, восьмая, двенадцатая
и т.д. гармоники). Комплексная передаточная
функция цепи (рис. 1.17, а) определяется
по формуле
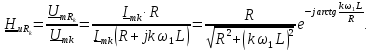
|
При |
k=0
|
|
|
|
k=1
|
|
|
|
k=2
|
|
|
|
k=3
|
|
|
|
k=4
|
|
|
|
k=5
|
|
|
|
k=6
|
|
|
|
k=7
|
|
|
|
k=8
|
|
|
|
k=9
|
|
|
|
k=10
|
|

Рис. 1.18. Спектры амплитуд последовательности прямоугольных импульсов и напряжения на резисторе в RL-цепи и коэффициенты передачи цепи
График зависимости коэффициента передачи RL-цепи от частоты изображен на рис. 3.18 (б).
Спектр
амплитуд
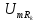 напряжения на резисторе, рассчитываем
в виде:
напряжения на резисторе, рассчитываем
в виде:
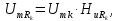 принимает
значения:
принимает
значения:
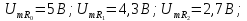
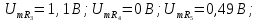
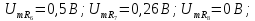
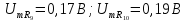
и приведен на рис. 1.18 (в).

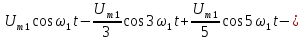
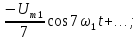
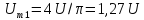
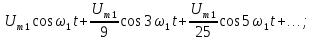
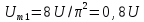


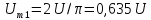
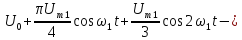

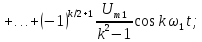

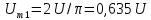
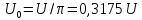

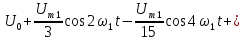
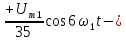
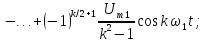
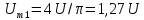




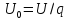 ;
;
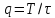 ;
;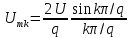
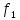 =0,5
кГц,
=0,5
кГц,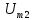 =3,28
В;
=3,28
В; =0,75
кГц,
=0,75
кГц,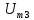 =1,5
В;
=1,5
В;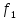 =1
кГц,
=1
кГц,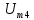 =0
В;
=0
В; =1,25
кГц,
=1,25
кГц,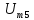 =0,9
В;
=0,9
В;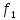 =1,5
кГц,
=1,5
кГц,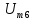 =1,06
В;
=1,06
В;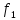 =1,75
кГц,
=1,75
кГц, =0,64
В;
=0,64
В;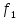 =2,0
кГц,
=2,0
кГц,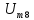 =0
В;
=0
В;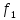 =2,25
кГц,
=2,25
кГц,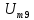 =0,5
В;
=0,5
В;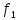 =2,5
кГц,
=2,5
кГц,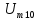 =0,64
В.
=0,64
В.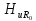 =1;
=1;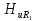 =0,95;
=0,95;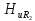 =0,85;
=0,85;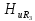 =0,73;
=0,73;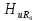 =0,62;
=0,62;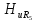 =0,54;
=0,54; =0,47;
=0,47;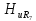 =0,41;
=0,41;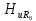 =0,37;
=0,37;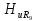 =0,33;
=0,33;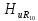 =0,3.
=0,3.