
- •Строительная механика.
- •Динамика систем с конечным числом степеней свободы масс
- •Динамика систем с конечным числом степеней свободы масс
- •Динамика систем с конечным числом степеней свободы масс
- •Динамика систем с конечным
- •Динамика систем с конечным
- •Динамика систем с конечным
- •Динамика систем с конечным
- •Динамика систем с конечным
- •Динамика систем с конечным
- •Динамика систем с конечным
- •Динамика систем с конечным
- •Динамика систем с конечным
- •Динамика систем с конечным числом степеней свободы масс
- •Динамика систем с конечным числом степеней свободы масс
- •Динамика систем с конечным числом степеней свободы масс
- •Динамика систем с конечным числом степеней свободы масс
- •Динамика систем с конечным числом степеней свободы масс
- •Динамика систем с конечным числом степеней свободы масс
- •Динамика систем с конечным числом степеней свободы масс
- •Динамика систем с конечным числом степеней свободы масс
- •Динамика систем с конечным числом степеней свободы масс
- •Динамика систем с конечным числом степеней свободы масс
- •Динамика систем с конечным числом степеней свободы масс
- •Динамика систем с конечным числом степеней свободы масс
- •Динамика систем с конечным числом степеней свободы масс

Строительная механика.
Часть III
ДИНАМИКА
СООРУЖЕНИЙ
ДИНАМИКА СИСТЕМ
С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ МАСС
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Динамика систем с конечным |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
числом |
степеней свободы масс |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
1 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
– для плоской |
||||||||||||||
|
|
|
|
|
|
|
n = nc = n + n |
|
|
|
n = |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нт.м. |
|
|
системы |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3n |
|
– для прост- |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для С помощью |
|
|
|
|
|
|
|
|
|
|
|
нт.м. |
|
ранственной |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
неточечных шарнирной |
|
|
|
|
|
|
|
|
|
|
системы |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
масс системы |
|
|
|
n |
|
– количество неточеч- |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нт.м. |
|
|
|
ных масс |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n = |
|
2nм – для плоской |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
системы |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n = 2 |
|
|
|
|
|
|
|
|
|
|
3nм – для простран- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ственной |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
системы |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n – количество сосре- |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
м доточенных масс |
|||||||||||
|
|
|
|
|
|
а) без учёта продольных |
|
|
n = б) с учётом продольных |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
деформаций стержней |
|
|
|
|
|
|
|
|
|
|
|
|
|
деформаций стержней |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n = 5 |
n = 8 |
n = 7 |
n = 1 |
|
0 |

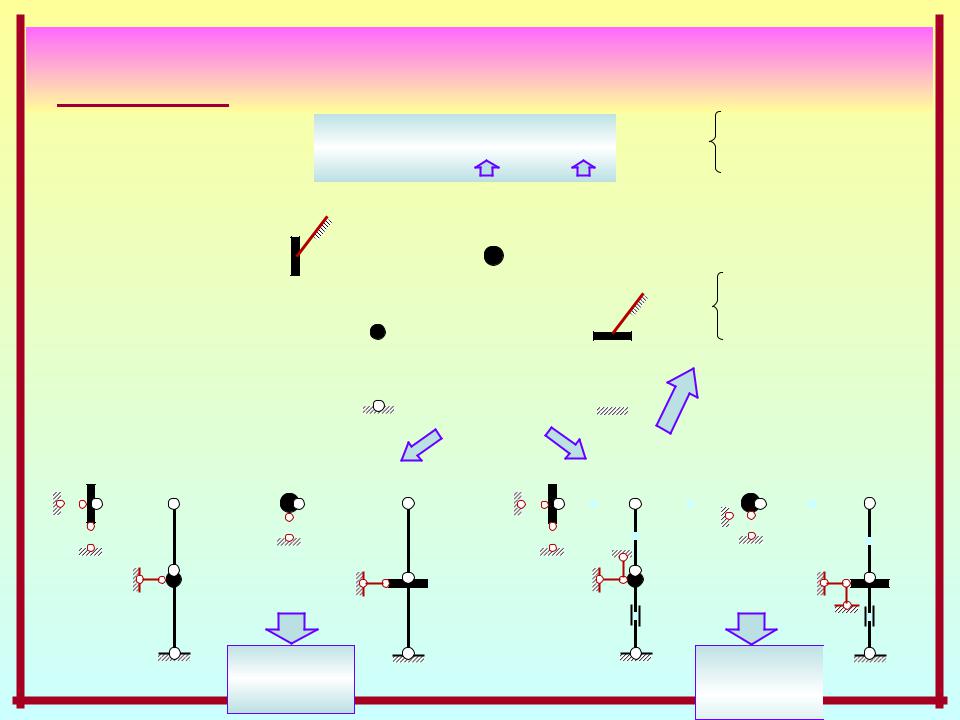
Динамика систем с конечным числом степеней свободы масс
Свободное движение
Предпосылки и рабочие гипотезы –
( в рамках линейной теории динамических расчётов ):
1. Рассматриваются линейно деформируемые системы.
2.Массы сосредоточенные, элементы системы невесомые.
3.Сопротивление внешней среды и внутреннее трение в системе
учитываются по модели вязкого трения.
4.Исследуется движение системы относительно её исходного состояния,
вкачестве которого принимается состояние равновесия, вызванное статическими воздействиями.
5.Определению подлежат динамические составляющие
напряжённо-деформированного состояния движущейся системы ( перемещения, усилия, напряжения, деформации ).
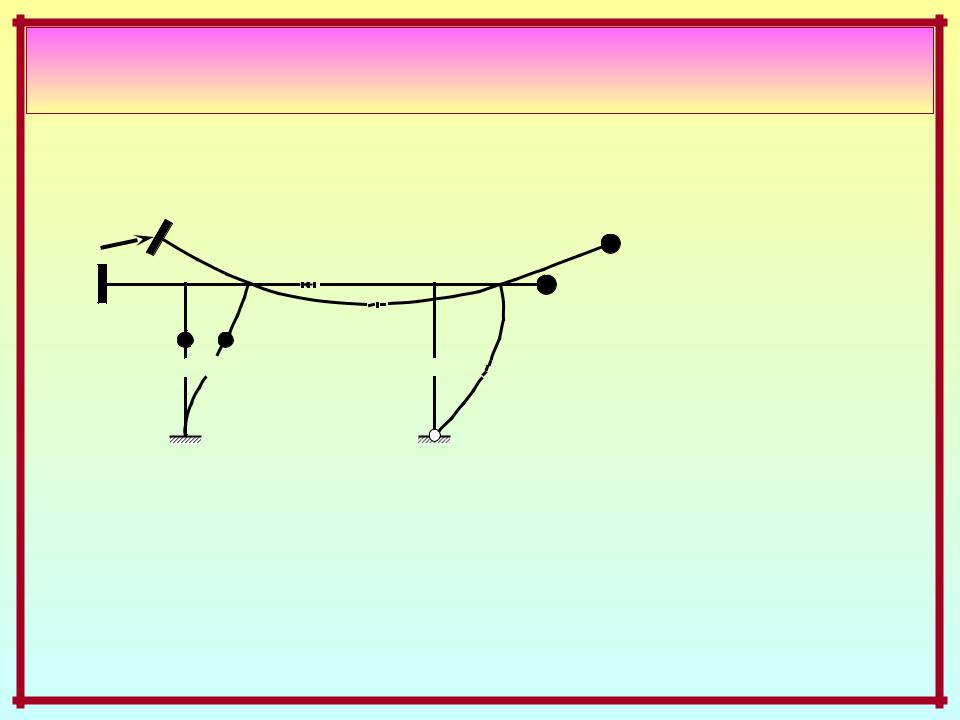
Динамика систем с конечным числом степеней свободы масс
Свободное движение
F0
ИсходноеНачальное(условно
 н
н едеформированноевозмущение )
едеформированноевозмущение ) 
состояние
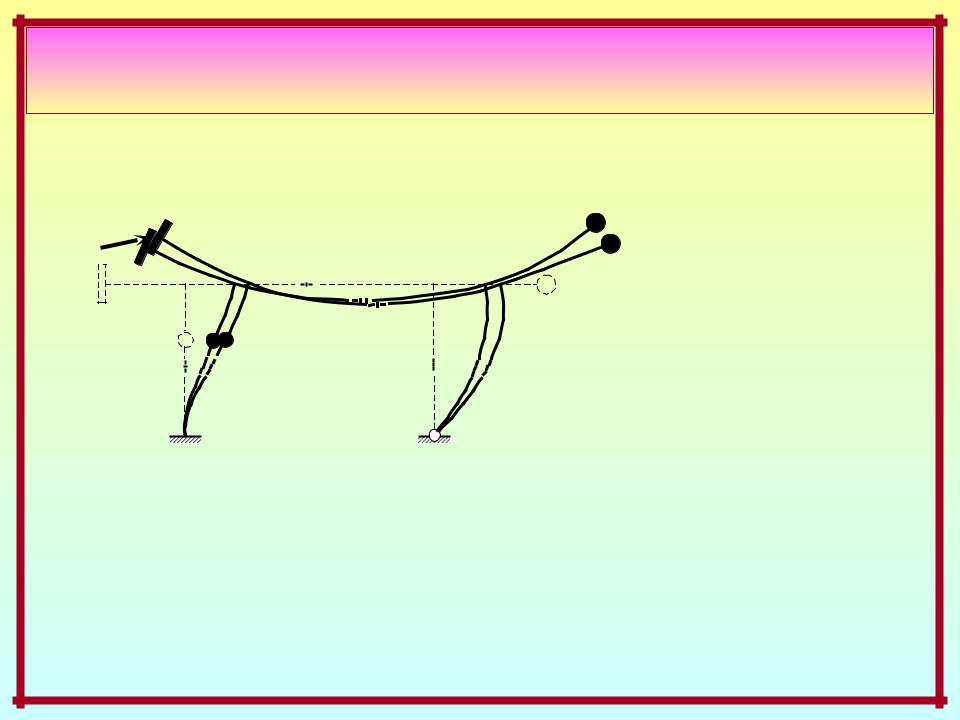
Динамика систем с конечным числом степеней свободы масс
Свободное движение
F0
Начальное
возмущение
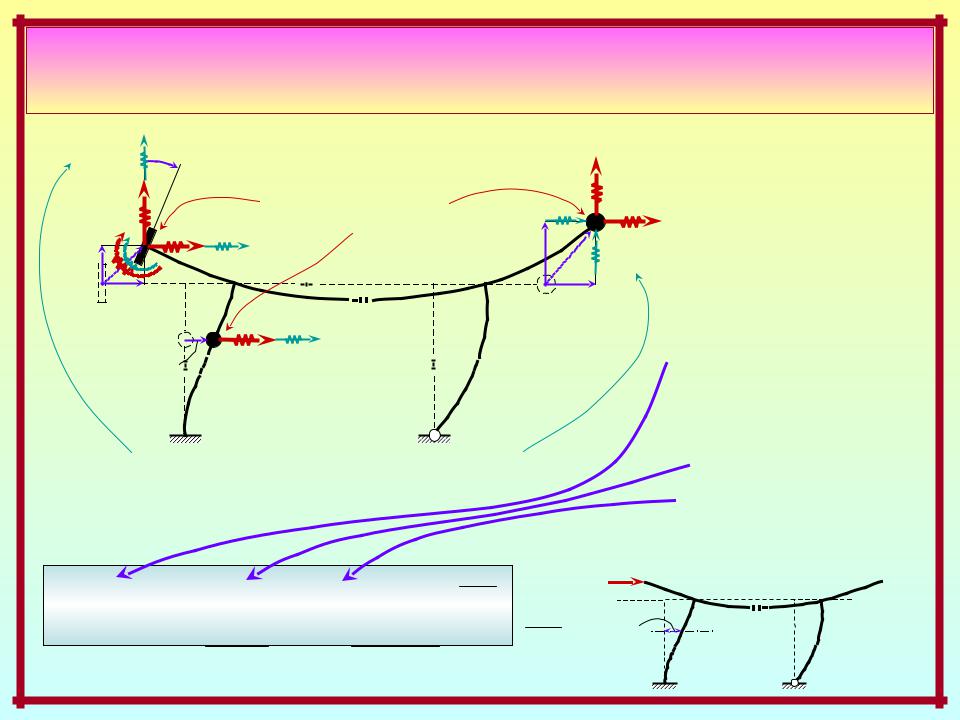
Динамика систем с конечным |
|
|
|||||||||||||||||||
числом степеней свободы масс |
|||||||||||||||||||||
FD,1 (t) |
y2 (t) |
Свободное движение |
|
|
|
|
|
||||||||||||||
J1 (t) |
|
|
|
По принципу |
|
Jn (t) |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
J |
|
(t) |
На основании |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
J2 (t) |
|
Jk (t) |
|
|
Д’Аламбера |
yn (t) |
|
|
|
||||||||||||
|
|
FD,k (t) |
|
|
|
|
FD,n (t) |
n-1 |
|
|
принципа |
|
|||||||||
y1 (t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
суперпозиции: |
||||||
(t) |
|
|
|
|
|
|
|
|
|
yn-1 (t) |
yi (t) yiJ (t) yiFD (t) |
||||||||||
y |
|
|
Ji (t) F (t) |
|
|
|
|||||||||||||||
|
|
|
|
|
n |
|
|
(t) n yiF |
|
|
|||||||||||
k |
|
|
|
|
|
|
|
|
|
yiJ |
D,k |
(t) |
|||||||||
|
|
|
|
|
|
|
D,i |
|
|
|
|
|
|
|
k |
|
|
|
|||
|
|
yi (t) |
В произвольный |
|
|
|
|
|
k 1 |
|
|
k 1 |
|
|
|||||||
|
|
|
|
|
|
От инерцион- |
От сил |
||||||||||||||
|
|
|
момент движения |
|
|
|
|
ных силовых |
сопротив- |
||||||||||||
|
|
|
|
|
|
( t ) |
|
|
|
|
|
|
факторов J(t) |
ления |
FD (t) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
yiJk |
(t) δik Jk (t) |
|
||||||
С учётом внешнего и внутреннего трения |
|
|
|
||||||||||||||||||
|
|
( FD (t) – |
силы сопротивления ) |
|
|
|
yiFD,k |
(t) δik FD,k (t) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ik – перемещение в заданной системе |
|
|||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
по направлению J |
от J |
= 1 (F |
= 1) |
||||||
|
|
|
|
|
|
|
|
|
|
|
Jk = 1 |
|
|
|
i |
k |
D,k |
|
|||
|
|
S |
|
|
|
|
u |
|
, |
i 1,n |
|
|
|
|
|
|
|
|
|||
yi (t) m δik Jk |
(t) FD,k (t) |
|
ik |
|
|
|
|
|
|
|
|
||||||||||
δik |
|
k 1 |
Si Sk |
ds |
|
Rj,i Rj,k |
, i,k 1,n |
|
|
Направ- |
|
|
|
||||||||
|
|
|
|
|
C |
|
|
|
|
|
ление Ji |
|
|
|
|||||||
C |
S |
|
|
j |
|
|
|
|
|
|
|
|
|
||||||||
поS j 1 l j |
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||

Динамика систем с конечным |
||||||||
числом степеней свободы масс |
||||||||
FD,1 (t) y2 |
(t) |
Свободное движение |
||||||
J1 (t) |
|
По принципу |
|
Jn (t) |
||||
|
|
Jn-1 (t) |
||||||
|
|
|
||||||
J2 (t) |
Jk (t) |
Д’Аламбера |
yn (t) |
|||||
y1 (t) |
|
FD,k (t) |
|
|
|
|
|
FD,n (t) |
|
|
|
|
|
|
|
yn-1 (t) |
|
yk (t) |
|
J (t) |
J |
(t) |
|
|
||
|
|
Ri (it) |
F |
i |
|
|
(t) |
|
|
|
|
(t) F |
|
||||
yi (t) |
|
|
D,i |
|
|
D,i |
|
|
В произвольный |
|
|
|
|||||
|
момент движения |
|
|
|
||||
|
|
( t ) |
|
|
|
|
|
|
С учётом внешнего и внутреннего трения ( FD (t) – силы сопротивления )
Другой способ |
|
|
|
вывода уравнений: |
|
|
|
yi (t) n δik Jk (t) FD,k (t) , |
i |
|
|
1,n |
|||
|
|
|
|
k 1 |
|
|
|
ik – перемещение в заданной системе
по направлению Ji от Jk = 1 (FD,k = 1)
Jk = 1
ik |
Направ- |
|
ление Ji |
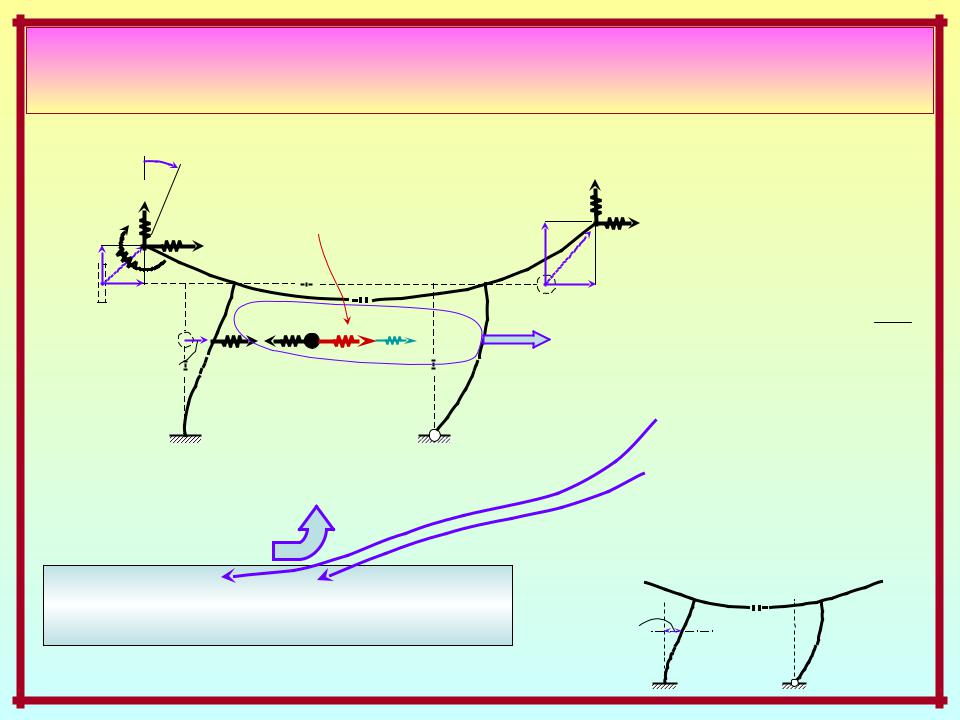
Динамика систем с конечным |
|||||||
числом степеней свободы масс |
|||||||
y2 (t) |
Свободное движение |
||||||
R1 (t) |
|
По принципу |
|
|
Rn (t) |
||
|
|
|
|
||||
R2 (t) |
|
|
|
Rn-1 (t) |
|||
Rk (t) |
Д’Аламбера |
yn (t) |
|
||||
y1 (t) |
|
|
|
|
|
|
|
|
|
|
|
|
yn-1 (t) |
||
yk (t) |
Ri (t) |
Ji (t) |
|
|
|||
|
FD,i (t) |
|
Ri (t) Ji (t) FD,i (t), i 1,n |
||||
yi (t) |
|
|
|
|
|||
В произвольный |
|
|
|
n |
|||
|
|
|
|
yi (t) yiR (t) |
|||
|
момент движения |
|
|
|
|||
|
|
|
|
k |
|||
|
|
|
( t ) |
|
|
|
k 1 |
|
|
|
|
|
|
yiRk (t) δik Rk (t) |
|
С учётом внешнего и внутреннего трения |
|||||||
( FD (t) – силы сопротивления ) |
|
δik Jk (t) FD,k (t) |
|||||
|
|
|
|
|
|
|
|
Другой способ |
|
|
|
вывода уравнений: |
|
|
|
yi (t) n δik Jk (t) FD,k (t) , |
i |
|
|
1,n |
|||
|
|
|
|
k 1 |
|
|
|
ik – перемещение в заданной системе
по направлению Ji от RJk=1 (FD,k = 1)
RJk = 1 































ik |
Направ- |
|
ление Ji |
Динамика систем с конечным |
|||||||||
числом степеней свободы масс |
|||||||||
FD,1 (t) |
y2 (t) |
|
Свободное движение |
|
|||||
J1 (t) |
|
|
|
|
|
|
Jn (t) |
|
|
|
|
|
|
|
|
|
Jn-1 (t) |
|
|
J2 (t) |
Jk (t) |
FD,k (t) |
|
yn (t) |
|
|
|
||
y1 (t) |
|
|
|
|
|
FD,n (t) По закону инерции: |
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
yk (t) |
|
|
Ji (t) |
|
|
yn-1 (t) |
Jk (t) mk yk (t) |
||
|
|
|
F |
(t) |
mk |
mk – если y |
(t) – линейное |
||
|
|
|
|
||||||
|
|
|
|
D,i |
|
|
k |
|
|
yi (t) |
В произвольный |
перемещение массы |
|||||||
|
Im,k – если yk(t) – угол по- |
||||||||
|
|
момент движения |
|
|
ворота неточечной |
||||
|
|
|
( t ) |
|
|
|
массы |
|
|
С учётом внешнего и внутреннего трения |
|
По модели Фойгта |
|||||||
( вязкого сопротивления ): |
|||||||||
|
D |
|
|
|
|
|
|
FD,k (t) k f,k yk (t) |
|
|
( F (t) – силы сопротивления ) |
|
|
|
|
||||
Дифференциальные уравнения |
ik – перемещение в заданной системе |
|||||||
свободного движения системы |
|
по направлению Ji от Jk = 1 |
||||||
|
n |
|
|
|
|
Jk = 1 |
|
|
с конечным числом степеней свободы масс |
|
|
||||||
с учётом вязкого сопротивления ) |
|
|
|
|
||||
yi (t) |
|
δik Jk (t) FD,k (t) , i 1,n |
|
|
|
|
||
n |
|
|
|
|
ik |
Направ- |
||
k 1 |
|
|
|
i 1,n |
||||
|
|
|
|
ление Ji |
||||
yi (t) δik mk yk (t) k f,k yk (t) , |
|
|||||||
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Динамика систем с конечным |
|
|
|||
|
числом степеней свободы масс |
|
|
|||
|
FD,1 (t) |
|
y2 (t) |
Свободное движение |
|
|
|
|
|
||||
|
|
|
|
|||
|
|
|
|
Jn (t) |
||
|
J1 (t) |
|||||
|
|
|
|
|||
J2 (t) |
Jk (t) |
FD,k (t) |
|
|
|
|
yn (t) |
|
|
Jn-1 (t) |
|
|
|
|
|
|||||
y1 (t) |
|
|
|
|
|
|
|
|
FD,n (t) |
|
По закону инерции: |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yk (t) |
|
Ji (t) |
|
|
|
|
|
|
yn-1 (t) |
|
|
Jk (t) mk yk (t) |
||||||||
|
|
|
F |
|
(t) |
|
|
|
mk |
mk |
– если y |
(t) – линейное |
||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
D,i |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
||
|
yi (t) |
В произвольный |
|
|
|
|
|
перемещение массы |
||||||||||||
|
|
|
|
|
Im,k |
– если yk(t) |
– угол по- |
|||||||||||||
|
|
момент движения |
|
|
|
|
|
|
ворота неточечной |
|||||||||||
|
|
|
( t ) |
|
|
|
|
|
|
A , |
|
– |
массы |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
из начальных |
|
|
|
||||||||
Решение системы |
|
n |
|
|
|
|
трения |
ij |
По0j |
модели Фойгта |
||||||||||
|
|
|
β t |
|
|
|
|
условий движения |
||||||||||||
С учетом внешнего и внутреннегоj |
( вязкого сопротивления ): |
|||||||||||||||||||
дифференциальных |
yi (t) |
Aij e |
|
sin(ω j t 0 j ) |
|
j – из дополнительного |
||||||||||||||
|
( R |
(t) – |
силы сопротивления ) |
|
|
F |
|
(t) k |
f,k |
y |
k |
(t) |
||||||||
|
уравнений:D |
|
|
|
|
|
|
|
|
|
|
D,k |
|
|
|
|
||||
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
( характеристического ) |
||||||
Дифференциальные уравнения |
|
|
|
|
|
уравнения |
|
|
|
|
||||||||||
ik – перемещение в заданной системе |
||||||||||||||||||||
свободного движения системы |
|
по направлению Ji от Jk = 1 |
|
|||||||||||||||||
с конечным числом степеней свободы масс |
Jk = 1 |
|
|
|
|
|
|
|
|
|
||||||||||
( с учётом вязкого сопротивления ) |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
n |
|
|
(t) k f,k |
|
|
i 1,n |
ik |
|
|
|
Направ- |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
ление Ji |
|
|
|
|
||||||||
yi (t) δik mk yk |
yk (t) , |
|
|
|
|
|
|
|
|
|||||||||||
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
