3.5. Структурная схема сар

Структурной называется схема САР, составленная из типовых

динамических звеньев. Эта схема показывает, из каких звеньев состоит САР и каким образом они соединены между собой.

На структурных схемах звенья условно изображаются прямоугольниками, внутри которых записываются их п6редаточные функции.

На рис. 3.20 представлена структурная схема САР температуры воздуха в помещении, рассмотренная в подразделе 3.1.

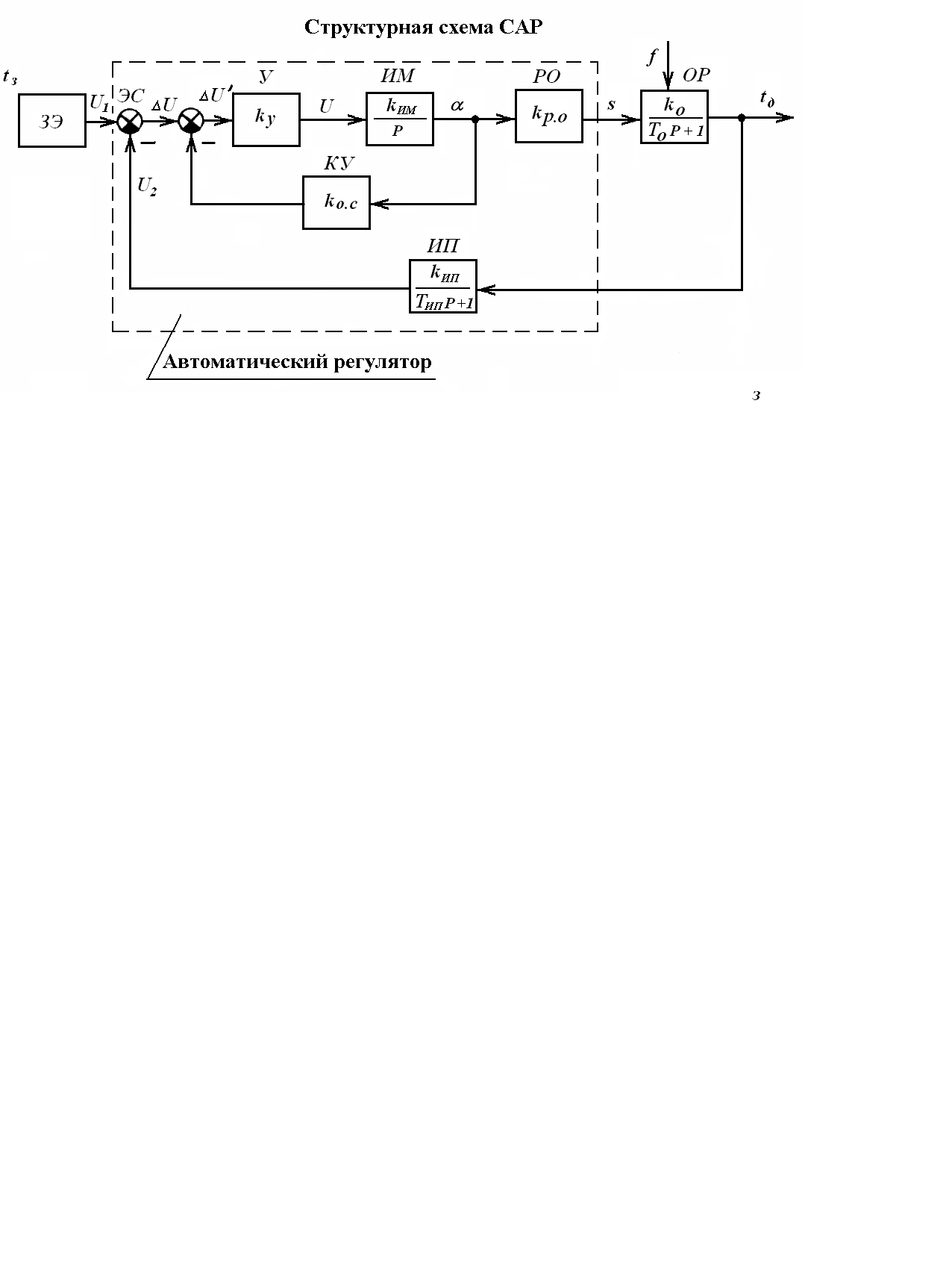
Рис. 3.20. Структурная схема САР температуры воздуха

в помещении

Основным достоинством структурной схемы САР является то, что она позволяет весьма просто и по единообразным правилам определять передаточные функции САР и их дифференциалные уравнения. Для этого применяются простейшие зависимости, по которым определяются простейшие функции соединений звеньев, сосстоящих из последовательных, параллельных и встречно-параллельных соединений звеньев.

Например, вначале можно определить передаточную функцию разомкнутой САР, а затем – замкнутой.

Передаточная функция разомкнутой САР (для САР без главной обратной связи (см. рис. 3.21))

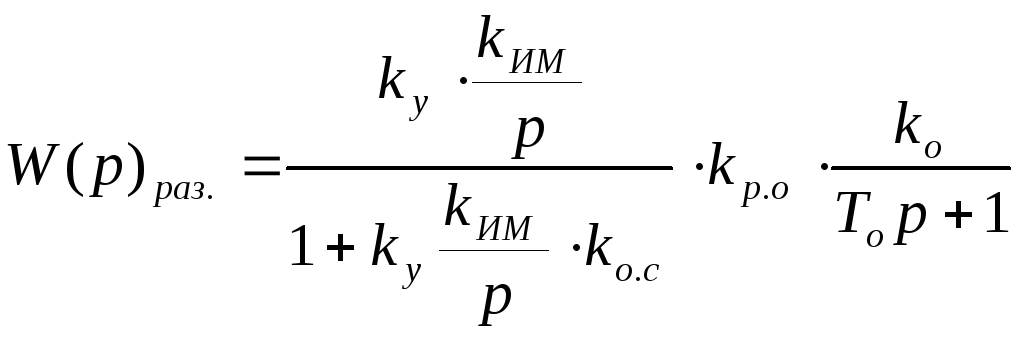. (3.39)

Передаточная функция замкнутой САР

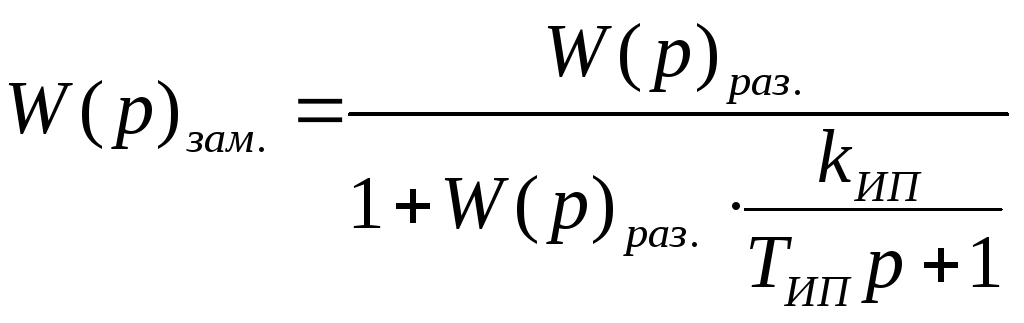
, (3.40)

или в общем виде после преобразования

. (3.41)

Из (3.41) можно увидеть, что замкнутая САР температуры воз-

духа в помещении описывается дифференциальным уравнением

третьего порядка (см. знаменатель в (3.41)).

Передаточная функция замкнутой САР необходима для оцен-

ки устойчивости и качества регулирования линейных систем.

3.6. Устойчивость линейных сар

Устойчивостью называется свойство системы регулирования возвращаться в исходный или близкий к нему режим после выхода из него в результате какого-либо воздействия.

Устойчивость – это важнейшее условие работоспособности САР.

Примеры устойчивой и неустойчивой САР с колебательным переходным процессом приведены на рис. 3.21.

Из рис. 3.21 видно, что по кривым переходных процессов, полученным экспериментально, можно ответить на вопрос устойчивости САР. Однако не во всех случаях возможно такое экспериментальное определении устойчивости. При проектировании САР это вообще невозможно. Поэтому на практике пользуются аналитическими методами устойчивости САР.

При аналитическом исследовании устойчивости за основу принимают дифференциальное уравнение, описывающее динамические свойства САР.

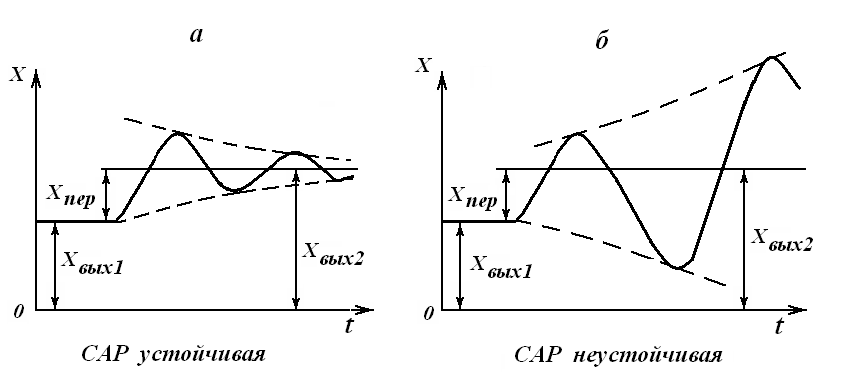
Рис. 3.21. Переходные характеристики устойчивой и

неустойчивой САР

В общем виде такое уравнение

(3.42)

Данное уравнение чаще всего определяют из передаточной функции замкнутой САР, так как 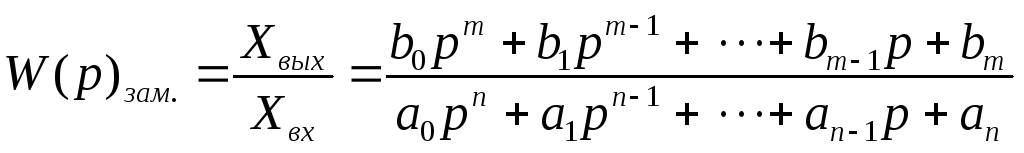. (3.43)

Способы получения передаточной функции изложены в подраз-

деле (3.3).

Если правую часть дифференциального уравнения приравнять нулю (т.е. исключить возмущающее воздействие), то можно получить однородное дифференциальное уравнение, описывающее свободное движение САР:

()X_св (p) = 0, (3.44)

где (p) – операторное изображение выходной величины для составляющей свободного движения системы.

Выражение, стоящее в скобках и приравненное нулю, называется характеристическим уравнением системы

() = 0. (3.45)

Из (3.45) видно, что левая часть характеристического уравнения представляет собой знаменатель передаточной функции замкнутой САР (3.41).

Характеристическое уравнение САР является исходным при исследовании устойчивости системы регулирования.

Исследование устойчивости на практике проводят с помощью критериев устойчивости, которые позволяют по коэффициентам характеристического уравнения решить вопрос устойчивости. При этом решения дифференциального уравнения не требуется.

Критерии устойчивости могут быть разделены на алгебраические и частотные [20]. С математической точки зрения все критерии устойчивости эквивалентны, однако, целесообразный выбор того или иного критерия устойчивости при решении конкретных задач позволяет провести исследование устойчивости наиболее простым путем.

Алгебраические критерии устойчивости – позволяют судить об устойчивости системы по коэффициентам характеристического уравнения (3.44).

Критерии устойчивости Рауса и Гурвица позволяют по коэффициентам характеристического уравнения без вычисления его корней сделать вывод об устойчивости системы. Английский математик Э. Раус в 1877 г. сформулировал условие устойчивости в виде таблиц, а немецкий математик А. Гурвиц в 1895 г. разработал алгебраический критерий устойчивости в форме определителей, составленных из коэффициентов характеристического уравнения системы.

Следует заметить, что критерий Гурвица можно получить из критерия Рауса, поэтому иногда критерий Гурвица называют критерием Рауса – Гурвица.

Критерий устойчивости Рауса – Гурвица. Из коэффициентов характеристического уравнения (3.45) строят сначала главный определитель Гурвица (3.46) по следующему правилу: по главной диагонали определителя слева направо выписывают все коэффициенты характеристического уравнения от дов порядке возрастания индексов. Столбцы вверх от главной диагонали дополняют коэффициентами характеристического уравнения с последовательно возрастающими индексами, а столбцы вниз – коэффициентами с последовательно убывающими индексами. На место коэффициентов с индексами большеn (n – порядок характеристического уравнения) и меньше нуля проставляют нули.

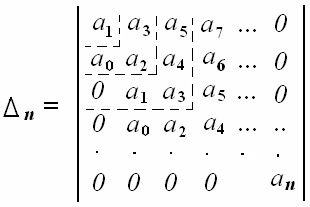
(3.46)

Отчеркивая в главном определителе Гурвица, как показано пунктиром, диагональные миноры, получаем определители Гурвица низшего порядка:

(3.47)

Номер определителя Гурвица определяется номером коэффициента по диагонали, для которого составляют данный определитель.

Критерий устойчивости Гурвица формулируется следующим образом: для того чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы все определители Гурвица имели знаки, одинаковые со знаком первого коэффициента характеристического уравнения , т.е. прибыли положительными.

Критерий устойчивости Гурвица обычно применяют при n ≤ 4. При n ≥ 5 целесообразно при использовании критерия устойчивости Гурвица переходить к численным методам с использованием ЭВМ.

Частотные критерии устойчивости позволяют судить об устойчивости систем автоматического управления по виду их частотных характеристик. Эти критерии являются графоаналитическими и получили широкое распространение, так как позволяют сравнительно легко исследовать устойчивость систем высокого порядка, а также имеют простую геометрическую интерпретацию и наглядность.

Критерий устойчивости Михайлова. Этот частотный критерий устойчивости, сформулированный в 1938 г. советским ученым А.В. Михайловым позволяет судить об устойчивости системы на основании рассмотрения некоторой кривой, называемой кривой Михайлова.

Пусть дано характеристическое уравнение системы четвертого порядка

. (3.56)

Представим данное уравнение в комплексной форме. Для этого оператор заменим на, так как, исходя из преобразования Лапласа,(часто обозначают) является комплексным числом.

Тогда, заменив левую часть уравнения (3.55) на комплексный полином ,на, получим

(3.57)

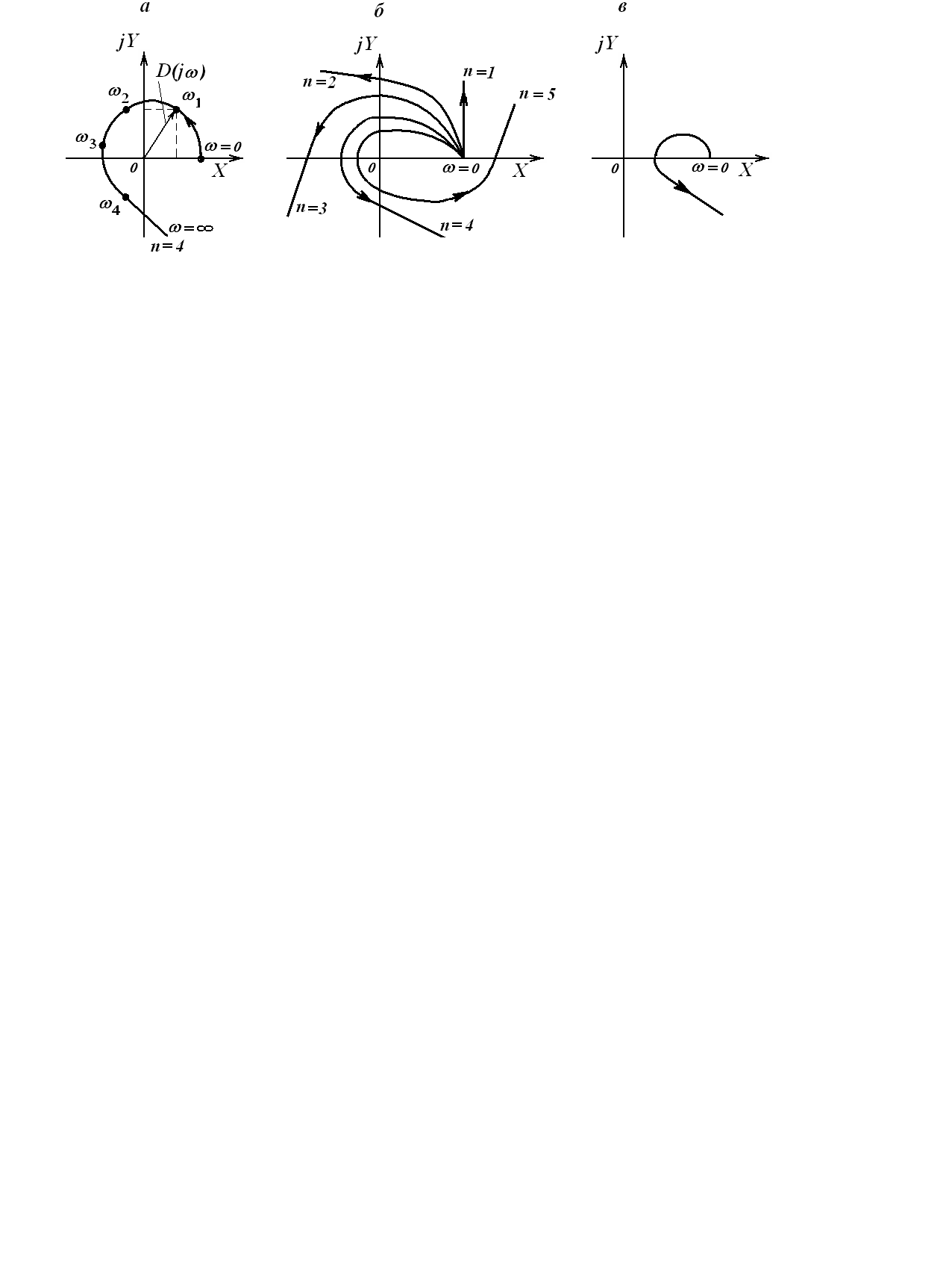где– годограф вектора (т.е. кривая, описанная концом вращающегося вектора на комплексной плоскости);– символ, показывающий, что рядом с ним стоящее действительное число откладывается на оси мнимых чисел.

Символ имеет значения:

(3.58)

Тогда

(3.59)

Выделим вещественную и мнимую части уравнения (3.58):

(3.60)

где иназывают соответственно вещественной и мнимой функциями Михайлова; функцииипредставляют собой модуль и фазу (аргумент) вектора

При изменении частоты от 0 довектор, изменяясь по величине и направлению, будет описывать своим концом в комплексной плоскостинекоторую кривую, называемуюкривой (годографом) Михайлова (рис. 3.22).

Для устойчивости САР требуется, чтобы кривая Михайлова проходила последовательно столько квадрантов, какова степень характеристического уравнения. При этом кривая Михайлова должна огибать начало координат против часовой стрелки (см. рис. 3.22).

Для устойчивости САР требуется, чтобы кривая Михайлова проходила последовательно столько квадрантов, какова степень характеристического уравнения. При этом кривая Михайлова должна огибать начало координат против часовой стрелки (см. рис. 3.22).

Также к частотным относится: критерий устойчивости Найквиста, разработанный в 1932 г. американским ученым Г. Найквистом, позволяющий судить об устойчивости замкнутой системы по виду амплитудно-фазовой характеристики разомкнутой системы; метод основанный на анализе логарифмических частотных характеристик и др. [20].

Рис. 3.22. Кривые Михайлова для устойчивых систем (а и б) и для неустойчивой системы (в)