
ФИЗИКА3 БОЛЬШЕ ГОТОВОГО1 / 1-st / Заготовки / работа 12
.docМинистерство общего и профессионального образования РФ
Санкт – Петербургский государственный горный институт
имени Г.В. Плеханова (технический университет)
Кафедра
общей и технической физики
ЛАБОРАТОРИЯ МЕХАНИКИ
РАБОТА 12
определение момента инерции
твердых тел с помощью маятника максвелла
САНКТ - ПЕТЕРБУРГ
1999
Цель работы - изучение маятника Максвелла и определение с его помощью момента инерции твердых тел.
Общие сведения
Момент инерции тела является мерой инертности тела при вращательном движении, подобно тому как масса тела является мерой инертности тела при поступательном движении. Момент инерции тела зависит от распределения массы тела относительно оси вращения . Для вычисления момента инерции твердого тела относительно данной оси разобьем мысленно тело на большое число весьма малых элементов - материальных точек . Тогда момент инерции тела
![]()
или
![]() ,
,
где mi - масса элемента; ri - расстояние от элемента до оси вращения; - плотность вещества в элементе объема dV, находящегося на расстоянии r от оси вращения. Таким образом, задача нахождения момента инерции сводится к интегрированию.
В данной работе момент инерции определяется экспериментально с помощью маятника Максвелла.
Рис.1
Рис.1
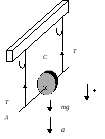
Выведем расчетную формулу для момента инерции маятника на основе закона сохранения энергии. Когда маятник поднят на высоту h, его полная энергия состоит только из потенциальной энергии Eп = mgh. В наинизшем положении маятника Eп = 0, а полная энергия равна сумме кинетических энергий поступательного и вращательного движений:
![]() .
.
Из закона сохранения энергии следует, что полная энергия маятника в верхнем и нижнем положениях должна быть одинакова, т.е.
![]() .
.
Отсюда момент инерции
![]() (1)
(1)
Поскольку поступательное движение маятника возникает только за счет вращательного, то угловая () и линейная (v) скорости связаны соотношением
![]() .
(2)
.
(2)
Подставив уравнение (2) в (1), получим
![]() .
(3)
.
(3)
Для равнопеременного движения связь между h, v и t может быть записана в виде
![]() .
.
Подставив выражение для v в формулу (3), получим окончательно
![]() .
(4)
.
(4)
Формулу (4) можно было бы вывести и на основе уравнений динамики для поступательного и вращательного движения.
Порядок выполнения работы
О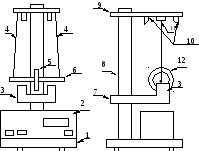 бщий
вид установки представлен на рис.2. В
основании 1 закреплена колонка 2, к
которой прикреплен неподвижно верхний
кронштейн 9 и подвижный нижний кронштейн
7. На верхнем кронштейне находится
электромагнит 10 и фотоэлектрический
датчик 11, а на нижнем кронштейне –
бщий
вид установки представлен на рис.2. В
основании 1 закреплена колонка 2, к
которой прикреплен неподвижно верхний
кронштейн 9 и подвижный нижний кронштейн
7. На верхнем кронштейне находится
электромагнит 10 и фотоэлектрический
датчик 11, а на нижнем кронштейне –
Рис.2
фотоэлектронный датчик 3.
Маятник представляет собой диск 5, закрепленный на оси 6, подвешенной на двух нитях 4 (бифилярный подвес). На диск можно насаживать сменные кольца 12, изменяя таким образом момент инерции системы.
Маятник удерживается в верхнем положении электромагнитом 10. Фотоэлектрические датчики 3 и 11 соединены с электронным секундомером 2. Верхний электронный датчик задает момент начала движения маятника, а нижний - окончания движения (опускания) маятника.
Последовательность проведения измерений следующая:
1) включить в сеть сетевой шнур прибора и нажать кнопку «Сеть»;
2) надеть на диск маятника одно из колец (если оно не надето);
3) отрегулировать длину нити так, чтобы в нижнем положении маятника край кольца находился примерно на 2 мм ниже оптической оси нижнего фотоэлектрического датчика (можно не менять длину нити, а переместить на нужную высоту подвижный нижний кронштейн);
4) если необходимо, произвести корректировку установки маятника так, чтобы его ось была параллельна основанию прибора;
5) проверить, находится ли кнопка «Пуск» в отжатом положении (т.е. включен ли электромагнит);
6) намотать на ось маятника нить подвески, обращая внимание на то, чтобы она наматывалась равномерно, виток к витку; в верхнем положении маятника должен быть зафиксирован электромагнитом;
7) нажать кнопки «Сброс» и «Пуск»;
8) снять отсчет времени падения маятника по прибору;
9) повторить пп.5-8 еще пять-десять раз;
10) по указанию преподавателя провести измерения еще с одним кольцом;
11) по измеренным значениям времени определить среднее значение времени падения маятника
![]()
и по шкале на вертикальной колонке прибора длину маятника h.
При обработке
результатов эксперимента вычислить
общую массу маятника
![]() ,
где m0
- масса
оси; mд
- масса диска; mк
- масса
кольца, и момент инерции маятника
,
где m0
- масса
оси; mд
- масса диска; mк
- масса
кольца, и момент инерции маятника
![]() ,
,
где R0 - радиус оси маятника.
Теоретическое значение момента инерции маятника
![]() ,
,
где J0
- момент инерции оси маятника,
![]() ;
Jк - момент
инерции кольца, надетого на диск,
;
Jк - момент
инерции кольца, надетого на диск,
![]() Jд
- момент инерции диска,
Jд
- момент инерции диска, ![]() Rд и Rк
- радиусы диска и кольца соответственно.
Rд и Rк
- радиусы диска и кольца соответственно.
Для полученного экспериментально значения момента инерции следует вычислить среднюю квадратическую погрешность
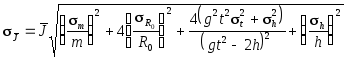 .
.
Затем
с учетом числа измерений n
для доверительной вероятности = 0,68
определить по таблице коэффициент
Стьюдента t (,
n) и рассчитать
![]() .
.
Записать окончательный
результат в форме
![]() ,
сравнить экспериментальное значение
J
с теоретическим Jт.
,
сравнить экспериментальное значение
J
с теоретическим Jт.
Контрольные вопросы
1. Что такое момент инерции материальной точки?
2. Что такое момент инерции твердого тела?
3. От чего зависит величина момента инерции твердого тела?
4. Каков принцип действия маятника Максвелла?
5. Какие силы вызывают поступательное движение маятника?
6. Момент каких сил вызывает вращательное движение маятника?
7. Вывести формулу для определения момента инерции с помощью маятника Максвелла.
