Спектральный тест
Для спектрального теста построены графики ДПФ последовательностей:
Преобразование Фурье последовательности, выработанной с помощью алгоритма маскирования (операция Xor), изображено на рис.3.8, где показаны первые 2000 отсчётов:
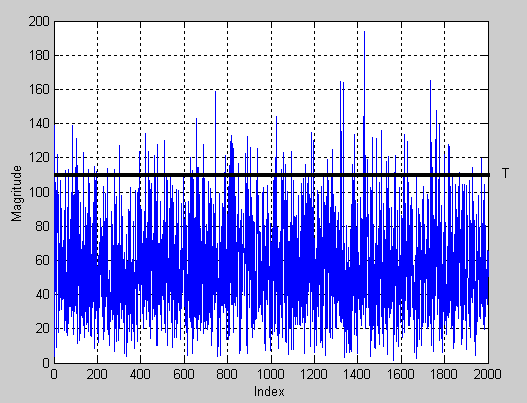
Рис. 3.8 ДПФ последовательности, выработанной с помощью алгоритма маскирования (операция Xor)
Преобразование Фурье последовательности, выработанной с помощью алгоритма маскирования (операция умножение) изображено на рис.3.9, где показаны первые 2000 отсчётов:
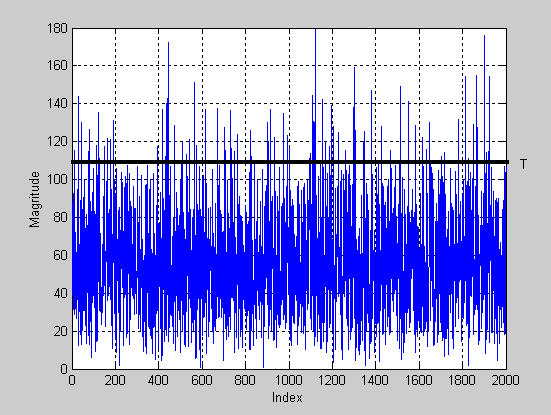
Рис. 3.9 ДПФ последовательности, выработанной с помощью алгоритма маскирования (операция умножение)
Преобразование Фурье последовательности, выработанной с помощью алгоритма маскирования (операция умножение (мод)) изображено на рис.3.10, где показаны первые 2000 отсчётов:
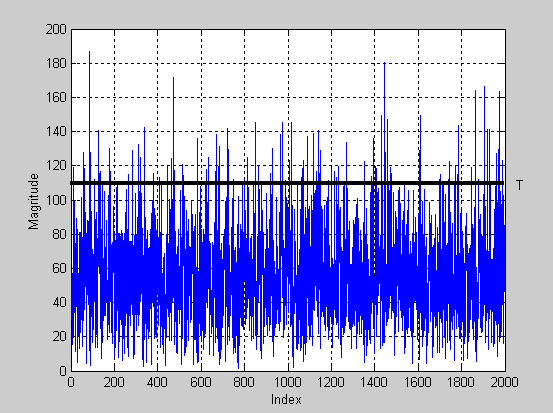
Рис. 3.10 ДПФ последовательности, выработанной с помощью модифицированного алгоритма маскирования (операция умножение)
Тест линейной сложности
Последовательность длиной 1000000 бит, выработанная с помощью алгоритма маскирования (операция Xor), была протестирована с помощью теста линейной сложности (The Linear Complexity Test) из пакета тестов национального института стандартов и технологий (НИСТ).
Линейная сложность последовательности – это минимальное число секций сдвигового регистра с линейной обратной связью (LFSR), который генерирует последовательность.
Для вычисления линейной сложности в тесте используется алгоритм Berlekamp-Massey.
Параметры тестирования:
n = 1000000 – длина последовательности в битах.
M = 1000 – длина одного блока в битах.
K = 6 – число степеней свободы.
Полученные результаты:
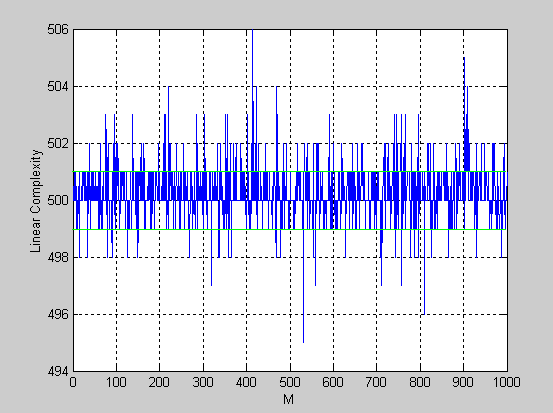
Рис. 3.11 Линейные сложности для 1000 блоков последовательности.
Как показывает рис. 3.11, большинство линейных сложностей имеют значения в окрестности 500, что говорит о том, что тестируемая последовательность очень близка к случайной, т.к. для случайной конечной последовательности длиной n линейная сложность близка к n/2.
Высокая линейная сложность не обязательно гарантирует стойкость генератора, но низкая линейная сложность явно указывает на недостаточную надёжность.
Тестовая статистика
.
Пропорциональность
Значение
v0 = 13; 0,013 0,01047
v1 = 23; 0,023 0,03125
v2 = 120; 0,120 0,125
v3 = 511; 0,511 0,5
v4 = 251; 0,251 0,25
v5 = 64; 0,064 0,0625
v6 = 18; 0,018 0,02078
Предполагается,
что распределение частоты Ti
(в
)
должно быть пропорционально
.
Р-значение = 0.7230.
Т.к. P-значение≥ 0.01, считаем последовательность случайной.
Для наиболее полного представления о характере генерируемой алгоритмом маскирования (операция Xor) последовательности, построимпрофиль линейной сложности.
Профиль линейной
сложности определяет линейную сложность
последовательности по мере её удлинения.
Для случайной конечной последовательности
длиной n
линейная сложность близка к n/2,
что можно видеть рис. 3.12. 
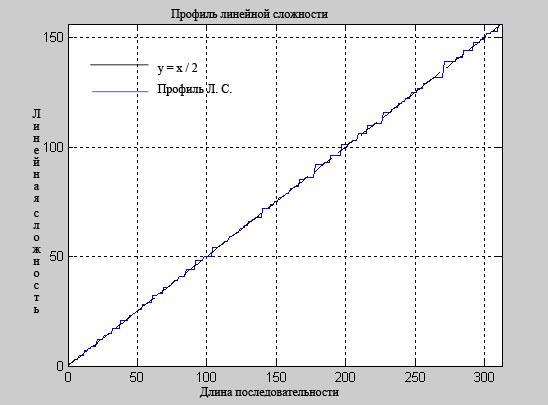
Рис. 3.12 Профиль линейной сложности для алгоритма маскирования (операция Xor).
Аналогичный тест был проведен для последовательности, выработанной с помощью алгоритма маскирования (операция умножение).
Параметры тестирования:
n = 1000000 – длина последовательности в битах.
M = 1000 – длина одного блока в битах.
K = 6 – число степеней свободы.
Полученные результаты:
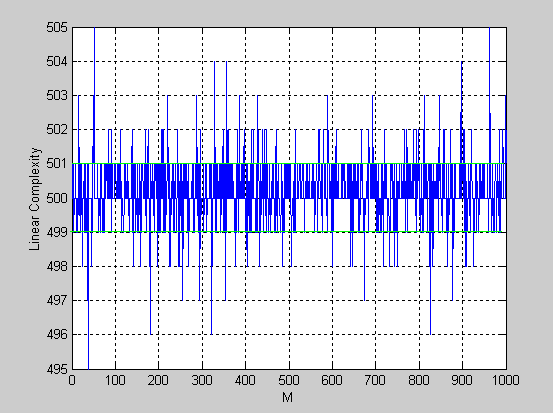
Рис.3.13 Линейные сложности для 1000 блоков последовательности.
Как показывает Рис. 3.13, большинство линейных сложностей также имеют значения в окрестности 500, что говорит о том, что тестируемая последовательность очень близка к случайной, т.к. для случайной конечной последовательности длиной n линейная сложность близка к n/2.
Тестовая статистика
.
Пропорциональность
Значение
v0 = 9; 0,009 0,01047
v1 = 29; 0,029 0,03125
v2 = 124; 0,124 0,125
v3 = 504; 0,504 0,5
v4 = 272; 0,272 0,25
v5 = 47; 0,047 0,0625
v6 = 15; 0,015 0,02078
Р-значение = 0.2515.
Т.к. P-значение≥ 0.01, считаем последовательность случайной.
Рис. 3.14 Профиль линейной сложности для алгоритма маскирования (операция умножение).
Аналогичный тест был проведен для последовательности, выработанной с помощью модифицированного алгоритма маскирования (операция умножение).
Параметры тестирования:
n = 1000000 – длина последовательности в битах.
M = 1000 – длина одного блока в битах.
K = 6 – число степеней свободы.
Полученные результаты:
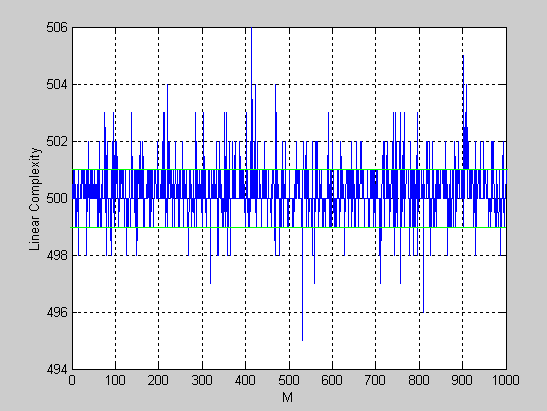
Рис.3.15 Линейные сложности для 1000 блоков последовательности.
Как показывает Рис. 3.15, большинство линейных сложностей также имеют значения в окрестности 500, что говорит о том, что тестируемая последовательность очень близка к случайной, т.к. для случайной конечной последовательности длиной n линейная сложность близка к n/2.
Тестовая статистика
.
Пропорциональность
Значение
v0 = 6; 0,006 0,01047
v1 = 25; 0,025 0,03125
v2 = 116; 0,116 0,125
v3 = 508; 0,508 0,5
v4 = 260; 0,260 0,25
v5 = 60; 0,060 0,0625
v6 = 25; 0,025 0,02078
Р-значение = 0.5099.
Т.к. P-значение≥ 0.01, считаем последовательность случайной.
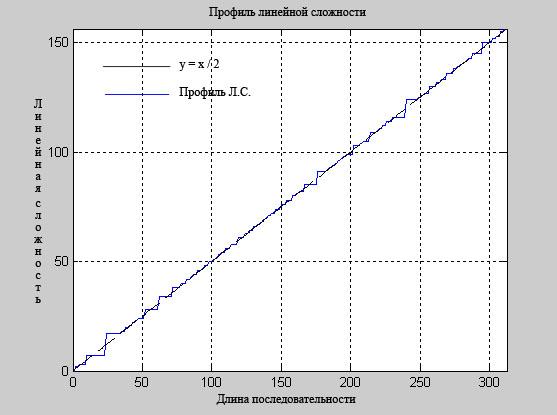
Рис. 3.16 Профиль линейной сложности для алгоритма маскирования (операция умножение).