To Students / Алгоритм Форда-Фалкерсона. Поримеры

Потоки в сетях. Алгоритм Форда – Фалкерсона. Пусть – ориентированный граф без петель и без кратных дуг, имеющий единственный источник, обозначенный , и единственный сток, обозначенный . Все остальные вершины графа будем называть промежуточными. Если каждой дуге графа поставлено в соответствие неотрицательное число (пропускная способность дуги), то говорят, что задана транспортная сеть (или просто сеть) .

Функция , определённая на множестве дуг орграфа и прини­мающая неотрицательные целые значения, называется потоком в сети , если выполняются следующие условия:

1) для любой дуги ;

2) для любой промежуточной вершины графа

,

где – множество вершин, к которым ведут дуги с началом в вершине , и – множество вершин, из которых ведут дуги к вершине .

Величина называется потоком по дуге , а разность

называется дивергенцией потока в вершине .

Таким образом: 1) поток по каждой дуге не должен превышать её пропускной способности; 2) дивергенция потока в произвольной вершине (кроме источника и стока) равна нулю, т. е. сумма потоков по дугам, заходящим в произвольную промежуточную вершину, равна сумме потоков по дугам, исходящим из этой вершины. Это означает, что поток не возникает и не накапливается в промежуточных вершинах.

Данная математическая модель описывает поведение газа или жидкости в трубопроводе, транспортные потоки в сети дорог, пересылку товаров на рынок по различным каналам и т. д.

Величиной потока называется сумма потоков по дугам, исходящим из источника: . Величина потока равна сумме потоков по дугам, заходящим в сток.

Поток в транспортной сети, имеющий наибольшую возможную величину, называется максимальным потоком. В одной и той же сети может быть несколько максимальных потоков (их величины, разумеется, совпадают). Задача о максимальном потоке состоит в следующем: в заданной сети найти поток максимальной величины.

Пусть – поток в сети . Дуга называется насыщенной, если поток по ней равен её пропускной способности: . Поток называется полным, если любой путь в сети из в содержит по крайней мере одну насыщенную дугу. Всякий максимальный поток является полным.

Теорема 6.1. В каждой сети существует максимальный поток.

Определение 6.1. Цепью из вершины в вершину в сети называется последовательность попарно различных вершин и дуг, в которой любые два соседних элемента инцидентны. Если при этом дуга выходит из вершины и заходит в вершину , то она называется прямой дугой цепи. Если же дуга выходит из вершины и заходит в вершину , то она называется обратной дугой цепи.

Пусть – поток в сети и – цепь из в . Для каждой дуги цепи положим:

.

Определение 6.2. Цепь из вершины в вершину называется – дополняющей, если .

Алгоритм отыскания максимального потока в сети

0-й шаг. Построить произвольный поток в сети (можно и ну­левой).

-й шаг. Пусть – поток в сети к началу k-го шага. Для текущего потока ищется – дополняющая цепь . Если такой цепи нет, то максимальный поток найден: это . В противном случае, если – дополняющая цепь найдётся, то поток построится по следующему правилу:

Величина этого потока определяется равенством: .

6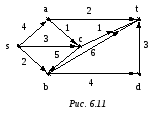.20. Построить максимальный поток в сети, изображённой на рис. 6.11.

6.20. На сетевом графике метка рядом с дугой означает: – пропускная способность дуги , – поток по дуге .

Шаг 0. Начальный поток: для любой дуги сети полагаем (рис. 6.25, а). Величина потока .

Шаг 1. Рассмотрим цепь . Для каждой дуги цепи вычисляем : . Цепь дополняющая. Строим поток : ; ; остальные дуги сети не входят в цепь , для таких дуг (рис. 6.25, b). Величина потока: .

Шаг 2. Рассмотрим цепь . Для каждой дуги цепи вычисляем ,

. Цепь дополняющая. Строим поток : ; ; остальные дуги сети не входят в цепь , для таких дуг (рис. 6.25, с). Величина потока: .

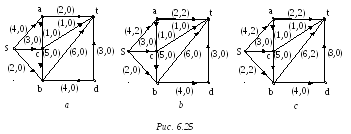
Шаг 3. Рассмотрим цепь . Для каждой дуги цепи вычисляем , . Цепь дополняющая. Строим поток :; ; ; остальные дуги сети не входят в цепь , для таких дуг (рис. 6.25, d). Величина потока: .

Шаг 4. Рассмотрим цепь . Для каждой дуги цепи вычисляем , . Цепь дополняющая. Строим поток : ; ; ; остальные дуги сети не входят в цепь , для таких дуг (рис. 6.25, е). Величина потока: .

Для сети, изображённой на рисунке 6.25, е, дополняющих цепей из вершины в вершину нет. Следовательно, поток является максимальным потоком и его величина равна 8.

6.21. Построить максимальный поток в сети, изображённой на рис. 6.12.

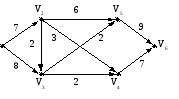
Рис. 6.12

6.21. Шаг 0. Начальный поток: для любой дуги сети полагаем (рис. 6.26, а). Величина потока .

Шаг 1. Рассмотрим цепь . Для каждой дуги цепи вычисляем . Цепь дополняющая. Строим поток ; ; остальные дуги сети не входят в цепь , для таких дуг (рис. 6.26, b). Величина потока: .

Шаг 2. Рассмотрим цепь . Для каждой дуги цепи вычисляем , . Цепь дополняющая. Строим поток ; ; ; остальные дуги сети не входят в цепь , для таких дуг (рис. 6.26, с). Величина потока: .

Шаг 3. Рассмотрим цепь . Для каждой дуги цепи вычисляем , . Цепь дополняющая. Строим поток ; ; ; остальные дуги сети не входят в цепь , для таких дуг (рис. 6.26, d). Величина потока: .

Шаг 4. Рассмотрим цепь . Для каждой дуги цепи вычисляем , . Цепь дополняющая. Строим поток ; ; ; остальные дуги сети не входят в цепь , для таких дуг (рис. 6.26, е). Величина потока: .

Для сети, изображённой на рис. 6.26, e, дополняющих цепей из вершины в вершину нет. Следовательно, поток является максимальным потоком и его величина равна 11.