
- •3. Магнетизм
- •3.1. Магнитное поле. Сила Лоренца
- •3.2. Движение заряженных частиц в электрических и магнитных полях
- •3.3. Сила Ампера
- •3.4. Рамка с током в магнитном поле
- •3.5. Эффект Холла
- •3.6. Вычисление магнитной индукции. Закон Био-Савара-Лапласа
- •3.7. Циркуляция и поток вектора магнитной индукции
- •3.8. Работа по перемещению контура с током в магнитном поле. Работа электродвигателя
- •3.9. Индуктивность
- •3.10. Закон электромагнитной индукции
- •3.11. Правило Ленца
- •3.12. Явления при замыкании и размыкании тока. Энергия магнитного поля
- •3.13. Генераторы и электродвигатели
- •3.14. Трансформаторы
- •3.15. Природа электромагнитной индукции
- •3.16. Магнитное поле в веществе
- •3.17. Теорема о циркуляции магнитного поля в веществе. Напряженность магнитного поля
- •3.18. Молекулярная теория магнетизма
- •3.19. Ток смещения. Уравнения Максвелла
- •3.20. Природа магнетизма
3.6. Вычисление магнитной индукции. Закон Био-Савара-Лапласа
Итак, мы научились рассчитывать силы, действующие на заряженные частицы и токи, находящиеся в магнитном поле. Сами магнитные поля тоже создаются какими-то движущимися зарядами. В этом параграфе мы начинаем обсуждение методов вычисления индукции магнитного поля.
Начнем
с магнитного поля, создаваемого в
пространстве единственным движущимся
со скоростью
![]() зарядом
зарядом![]() .
Этот закон является обобщением опытных
фактов и выражается формулой:
.
Этот закон является обобщением опытных
фактов и выражается формулой:
![]() (3.11)
(3.11)
где
![]()
это вектор, проведенный от заряда
это вектор, проведенный от заряда
![]() к точке, в которой вычисляется магнитное
поле
к точке, в которой вычисляется магнитное
поле![]() (точке наблюдения). Постоянная величина
(точке наблюдения). Постоянная величина![]() ,
Гн/м, называется магнитной постоянной.
,
Гн/м, называется магнитной постоянной.
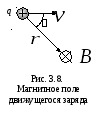
Движущийся
заряд создаёт магнитное поле во всём
окружающем пространстве. Направление
и модуль вектора
![]() зависят от точки наблюдения. В случае
положительного заряда направление
вектора
зависят от точки наблюдения. В случае
положительного заряда направление
вектора![]() совпадает с направлением векторного
произведения
совпадает с направлением векторного
произведения![]() ,
т.е. определяется правилом левой руки
(рис. 3.8).
,
т.е. определяется правилом левой руки
(рис. 3.8).
![]() ,
(3.11,а)
,
(3.11,а)
где
![]()
угол между направлением движения заряда
и вектором
угол между направлением движения заряда
и вектором
![]() .
.
![]() .
.
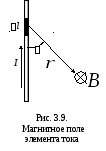
Пусть
по проводнику течет ток
![]() .
Вычислим магнитное поле, создаваемое
малым элементом тока
.
Вычислим магнитное поле, создаваемое
малым элементом тока![]() (рис. 3.9). Если
(рис. 3.9). Если![]()
средняя скорость упорядоченного
движения электронов, тогда согласно
уравнению (3.11,а) магнитное поле, создаваемое
в точке наблюдения одним электроном из
элемента тока:
средняя скорость упорядоченного
движения электронов, тогда согласно
уравнению (3.11,а) магнитное поле, создаваемое
в точке наблюдения одним электроном из
элемента тока:
![]() .
.
Все
свободные электроны элемента тока
создают поля, направленные за плоскость
чертежа (рис. 3.9), поэтому по принципу
суперпозиции величина суммарного поля
элемента тока:
![]() ,
где
,
где![]()
число свободных электронов в элементе
проводника
число свободных электронов в элементе
проводника
![]() .
Величину
.
Величину![]() можно выразить через концентрацию
свободных электронов:
можно выразить через концентрацию
свободных электронов:![]() ,
где
,
где![]()
объем элемента проводника,
объем элемента проводника,
![]()
сечение проводника. Таким образом:
сечение проводника. Таким образом:
![]() .
.
Учитывая,
что сила тока
![]() (см. уравнение (2.23)), получим:
(см. уравнение (2.23)), получим:
![]() . (3.12)
. (3.12)
Уравнение (3.12) определяет магнитное поле, создаваемое элементом тока, и представляет собой закон Био-Савара-Лапласа. Оно было впервые получено французскими физиками Био и Саваром на основании экспериментального материала при содействии математика Лапласа.
Закон
Био-Савара-Лапласа можно записать в
дифференциальной форме (переходя от
малого к бесконечно малому элементу
тока
![]() ):
):
![]() (3.12,а)
(3.12,а)
и в векторной форме:
![]() .
(3.12,б)
.
(3.12,б)
Вектор
![]() направлен вдоль тока.
направлен вдоль тока.
Рассмотрим примеры расчета магнитных полей при помощи закона Био-Савара-Лапласа.
Пример
3.3 Поле
прямого тока.
Найти
магнитное, создаваемое прямолинейным
отрезком провода с током
![]() в произвольной точке пространства.
в произвольной точке пространства.
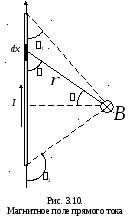
![]() ,
,![]() и расстояния
и расстояния![]() от точки наблюдения до проводника (см.
рис. 3.10). Разобьем весь отрезок провода
на малые элементы длины
от точки наблюдения до проводника (см.
рис. 3.10). Разобьем весь отрезок провода
на малые элементы длины![]() .
Поле одного малого элемента
.
Поле одного малого элемента![]() с координатой
с координатой![]() определяется согласно уравнению
(3.12,а):
определяется согласно уравнению
(3.12,а):
![]() .
.
Поле
в точке наблюдения – есть векторная
сумма полей, создаваемых каждым элементом.
Поля всех элементов направлены за
плоскость чертежа. Следовательно, для
того, чтобы определить величину поля,
надо просуммировать поля всех
элементов, или, «на языке математики»:
проинтегрировать уравнение (3.12,а). Для
этого в уравнении (3.12) нужно перейти к
одной переменной величине (переменной
интегрирования). Удобнее всего в качестве
переменной интегрирования взять угол
![]() (рис. 3.10). Выразим все переменные величины
в уравнении (3.12) через
(рис. 3.10). Выразим все переменные величины
в уравнении (3.12) через![]() .
.
Во-первых,
![]() .
Далее,
.
Далее,![]() .
Берем дифференциалы от обеих частей
этого равенства:
.
Берем дифференциалы от обеих частей
этого равенства:
![]()
![]()
![]()
![]()
![]() .
.
Таким
образом, для поля элемента
![]() получим:
получим:
 .
.
Осталось
выразить через
![]() переменную
переменную![]() :
:![]() .
Следовательно:
.
Следовательно:
![]() .
.
Теперь
интегрируем, учитывая, что все элементы
находятся в пределах углов
![]() от
от![]() (крайний нижний элемент) до
(крайний нижний элемент) до![]() (крайний верхний элемент):
(крайний верхний элемент):
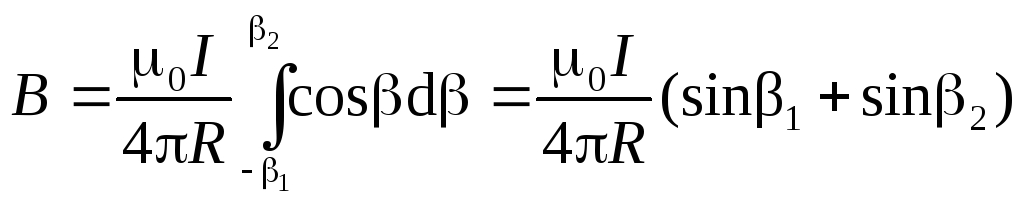 .
.
Переходя
вновь к углам
![]() и
и![]() ,
получим ответ:
,
получим ответ:
![]() . (3.13)
. (3.13)
Частным
случаем формулы (3.13) является поле
бесконечно длинного прямого провода
на расстоянии
![]() от него (
от него (![]() ,
,![]() ):
):
![]() . (3.14)
. (3.14)
Пример
3.4.
Магнитное
поле в центре кругового тока.
Найти
магнитную индукцию, создаваемую круговым
витком радиуса
![]() с током
с током![]() в центре витка.
в центре витка.
Решение.
Разобьем виток на малые элементы
![]() (рис. 3.11). Длину каждого элемента выразим
через радиус витка
(рис. 3.11). Длину каждого элемента выразим
через радиус витка![]() и соответствующий центральный угол
и соответствующий центральный угол![]() :
:![]() .
Тогда, согласно уравнению (3.12, а), магнитное
поле, создаваемое одним элементом тока
в центре витка (
.
Тогда, согласно уравнению (3.12, а), магнитное
поле, создаваемое одним элементом тока
в центре витка (![]() ,
,![]() ):
):
![]() .
.
![]() до
до![]() :
:
![]() .
(3.15)
.
(3.15)
Пример
3.5.
Магнитное
поле на оси кругового тока.
Найти магнитную индукцию, создаваемую
круговым витком радиуса
![]() с током
с током![]() в произвольной точке на оси витка.
в произвольной точке на оси витка.
Решение.
Разобьем виток на малые элементы
![]() (рис. 3.11). Длину каждого элемента выражаем
через радиус витка
(рис. 3.11). Длину каждого элемента выражаем
через радиус витка![]() и соответствующий центральный угол
и соответствующий центральный угол![]() :
:![]() .
Согласно уравнению (3.12,а) магнитное
поле, создаваемое одним элементом тока
в некоторой точке на оси витка, удаленной
на расстояние
.
Согласно уравнению (3.12,а) магнитное
поле, создаваемое одним элементом тока
в некоторой точке на оси витка, удаленной
на расстояние![]() от центра витка, (
от центра витка, (![]() ):
):
![]() .
.
Вектор
![]() перпендикулярен плоскости векторов
перпендикулярен плоскости векторов![]() и
и![]() (рис. 3.11). Вклады в общее магнитное поле
от отдельных элементов направлены в
разные стороны, поэтому суммировать
модули векторов
(рис. 3.11). Вклады в общее магнитное поле
от отдельных элементов направлены в
разные стороны, поэтому суммировать
модули векторов![]() нельзя.
нельзя.
Поскольку
результирующий вектор
![]() будет направлен вдоль оси
будет направлен вдоль оси![]() ,
он представляет собой сумму проекций
векторов
,
он представляет собой сумму проекций
векторов![]() на ось
на ось![]() :
:![]() .
Проекция вектора
.
Проекция вектора![]() на ось
на ось![]() :
:
![]() .
.
Интегрируем
по переменной
![]() :
:
![]() .
.
Учитывая, что
![]() ,
,
![]() ,
,
ответ можно представить в виде:
 . (3.16)
. (3.16)
![]() .
(3.17)
.
(3.17)
Величина
![]() называется поверхностной плотностью
тока. Она определяется для токов, текущих
по некоторым поверхностям. Поверхностная
плотность тока
это сила тока, приходящаяся на единицу
длины перпендикулярного току отрезка.
В нашем случае можно считать, что ток
идет по боковой поверхности соленоида.
Пусть соленоид имеет длину
называется поверхностной плотностью
тока. Она определяется для токов, текущих
по некоторым поверхностям. Поверхностная
плотность тока
это сила тока, приходящаяся на единицу
длины перпендикулярного току отрезка.
В нашем случае можно считать, что ток
идет по боковой поверхности соленоида.
Пусть соленоид имеет длину
![]() ,
состоит из
,
состоит из![]() витков, и по его обмотке течет ток
витков, и по его обмотке течет ток![]() .
Тогда полный ток, текущий по боковой
поверхности соленоида, равен
.
Тогда полный ток, текущий по боковой
поверхности соленоида, равен![]() ,
а поверхностная плотность тока
,
а поверхностная плотность тока![]() .
Формулу (3.17) можно переписать в виде:
.
Формулу (3.17) можно переписать в виде:
![]() .
(3.17,а)
.
(3.17,а)
В
случае, когда длина соленоида намного
превосходит его радиус (![]() ,
,![]() ),
),
![]() .
(3.18)
.
(3.18)
Формула (3.18) еще будет выведена в дальнейшем с помощью теоремы о циркуляции для магнитного поля. Будет показано, что магнитное поле внутри «длинных» соленоидов однородно, так, что формулу (3.18) можно использовать для расчета поля в любой точке внутри соленоида, а не только на его оси.
Во-первых, обратим внимание на то, что силовые линии магнитного поля всегда замкнуты. Вектор магнитной индукции направлен по касательной к линиям (рис. 3.13, а, б) в сторону, указываемую направлением стрелки на силовой линии.
В случае прямого тока (рис. 3.13, а) силовые линии представляют собой коаксиальные окружности с центрами на оси тока. Направление магнитной индукции в любой точке можно определить из закона Био-Савара-Лапласа, записанного в векторном виде (формула 3.12, б). Кроме того, для определения направлений силовых линий существует простое правило, называемое правилом буравчика или правого винта: при вращении буравчика в направлении силовых линий его поступательное движение совпадает с направлением тока.
В случае витка с током (рис. 3.13, б) или соленоида (рис. 3.13, в) направление магнитной индукции на оси витка или соленоида тоже можно определить по правилу буравчика. Направление магнитной индукции совпадает с направлением поступательного движения буравчика при его вращении по току.
Отметим, что картина силовых линий магнитного поля соленоида абсолютно идентична картине силовых линий полосового магнита (рис. 3.13, г). Концы соленоида тоже называют северным и южным полюсами. Силовые магнитные линии во внешнем пространстве соленоида или магнита идут от северного полюса к южному, а во внутреннем пространстве – наоборот.
