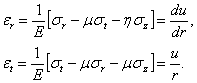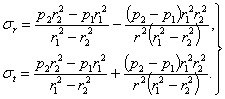Desktop / Документ Microsoft Office Word

Расчет толстостенных цилиндров.

Категория: Лекции по сопромату

   В тонкостенных цилиндрических резервуарах, подвергнутых внутреннему давлению, вполне возможно при вычислениях считать напряжения равномерно распределенными по толщине стенки. Это допущение мало отзывается на точности расчета.

   В цилиндрах, у которых толщина стенок не мала по сравнению с радиусом, подобное предположение повело бы к большим погрешностям. Расчет таких цилиндров дан Ляме и Гадолиным в 1852 — 1854 гг. Работы русского академика А. В. Гадолина в области расчета кривых стержней в применении к расчету прочности артиллерийских орудий создали ему мировую известность. Отечественные артиллерийские заводы (и многие зарубежные) до сих пор проектируют и изготовляют орудия, пользуясь исследованиями Гадолина.

   На Рис.1 изображено поперечное сечение толстостенного цилиндра с наружным радиусом , внутренним; цилиндр подвергнут наружному и внутреннему давлению .

Рис.1. Расчетная схема толстостенного цилиндра.

   Рассмотрим очень узкое кольцо материала радиусом внутри стенки цилиндра. Толщину кольца обозначим . Пусть АВ изображает небольшую часть этого кольца, соответствующую центральному углу .

   Размер выделенного элемента, перпендикулярный к плоскости чертежа, возьмем равным единице. Пусть и будут напряжения, действующие по внутренней и наружной поверхностям элемента АВ, a — напряжения по его боковым граням. По симметрии сечения цилиндра и действующей нагрузки элемент АВ перекашиваться не будет, и касательные напряжения по его граням будут отсутствовать. По граням элемента AB, совпадающим с плоскостью чертежа, будет действовать третье главное напряжение , вызванное давлением на днище цилиндра. Это напряжение можно считать постоянным по всем точкам поперечного сечения цилиндра.

   На элемент AB действуют в плоскости чертежа две силы coставляющие между собой угол , и радиальная сила, равная

   Эта сила направлена в сторону наружной поверхности. Уравновешиваясь, эти три силы составляют замкнутый треугольник abc (Рис.2).

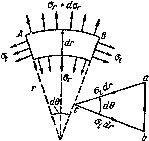Рис.2. Условия равновесия элемента кольца

   Из него следует, что радиальная сила, изображаемая отрезком ab, связана с силой (отрезок са) соотношением

или

;

пренебрегая малыми высшего порядка, получаем:

;

отсюда

(1)

   Условие равновесия дало только одно уравнение для нахождения двух неизвестных напряжений. Задача статически неопределима, и необходимо обратиться к рассмотрению деформаций. Деформация цилиндра будет заключаться в его удлинении и в радиальном, перемещении всех точек его поперечных сечений. Назовем радиальное перемещение точек внутренней поверхности рассматриваемого элемента через u(Рис.3). Точки наружной поверхности переместятся по радиусу на другую величину ; таким образом, толщина dr выделенного элемента увеличится на du, и относительное удлинение материала в радиальном направлении будет 

Рис.3. Геометрическая модель деформации элемента кольца

   В направлении напряжений относительное удлинение будет равно относительному удлинению дугиab, занявшей положение cd; так как относительное удлинение дуги таково же, как относительное удлинение радиуса r, то . По закону Гука

(2)

Так как и определяются одной и той же функцией и то они связаны условием совместности. Дифференцируем по r:

(3)

Это и будет условие совместности деформаций; заменяя в нем значения и по (2), получим второе уравнение, связывающее и :

или

(4)

Подставляя в это уравнение значение разности из (32.1), находим:

или

(5)

   Для совместного решения уравнений (1) и (5) продифференцируем первое по и подставим в него значение из второго; получим:

отсюда дифференциальное уравнение задачи:

(6)

Интеграл этого уравнения будет

(7)

что можно проверить подстановкой.

Постоянные А и В определятся из условий на внутренней и наружной поверхностях цилиндра:

(8)

   Знак минус в правых частях этих формул поставлен потому, что положительными мы приняли растягивающие напряжения (Рис.1).

Из условий (8) получаем:

Пользуясь этими значениями и уравнением (7), получаем окончательные формулы для и :

(9)

   Как видно из этих формул, сумма ( не зависит от r, т. е. относительная деформация вдоль оси цилиндра во всех точках сечения одинакова (так как и одинаково), и сечение остается плоским

Представляет очень большой практический интерес случай когда имеет место только одно внутреннее давление ; тогда

(10)

   График, изображающий распределение напряжений по толщине цилиндра в случае , дан на Рис.3. Так как по абсолютной величине продольное растягивающее напряжение обычно значительно меньше и то прочность цилиндра определяется этими последними. Применяя третью теорию прочности (наибольших касательных напряжений), получаем, что наибольшая разность главных напряжений, равная (для случая )

(11)

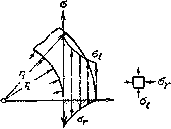Рис.3. Распределение напряжений по толщине цилиндра при 

будет иметь место в точках внутренней поверхности цилиндра и всегда будет по абсолютной величине значительно больше внутреннего давления.

   Таким образом, остаточные деформации появятся прежде всего у внутренней поверхности цилиндра, когда будет равно пределу текучести материала; борьба с их появлением путем увеличения наружного радиуса практически безнадежна, — с увеличением растут и числитель, и знаменатель формулы (11); поэтому разность главных напряжений хотя и убывает, но очень медленно. Однако момент появления пластических деформаций у внутренней поверхности цилиндра далеко не соответствует исчерпанию грузоподъемности конструкции; для правильной оценки прочности цилиндра необходимо перейти к расчету по допускаемым нагрузкам.

Рис.4. Динамика зоны текучести по толщине цилиндра

   Полное исчерпание грузоподъемности произойдет тогда, когда кольцевая пластическая зона, распространяясь от внутренней поверхности цилиндра, дойдет до наружной; состояние разрушения наступит тогда, когда материал у наружной поверхности достигнет состояния, при котором произойдет разрыв. На фиг. 544 показано отношение внутреннего давления , при котором пластическая зона охватывает все сечение, к давлению, соответствующему началу пластических деформаций . Оказывается, что действительная грузоподъемность значительно выше получаемой при обычном методе расчета.

   Упругая грузоподъемность толстостенных цилиндров может быть поднята путем создания начальных напряжений. Для этого необходимо изготовить цилиндр, составленный из двух цилиндров, вставленных один в другой; наружный диаметр внутреннего цилиндра делается несколько больше внутреннего диаметра наружного цилиндра; после одевания наружного цилиндра в нагретом состоянии на внутренний и его остывания по поверхности соприкасания возникнут реакция, сжимающие внутренний и растягивающие внешний цилиндры. Наличие этих начальных напряжений улучшает работу составного цилиндра при внутреннем давлении, как видно из приведенного ниже расчета.

   На Рис.5 изображен составной цилиндр после остывания. Напряжения в тангенциальном направлениибудут равны: для наружного цилиндра (растяжение)

для внутреннего цилиндра (сжатие)

Рис.5. модель составного цилиндра после остывания.

   Установим, какую разницу в радиусах надо дать, чтобы осуществить желательное начальное усилие ; — это начальный наружный радиус внутреннего цилиндра, а — начальный внутренний радиус наружного цилиндра.

   При остывании наружной трубы происходит выравнивание этих радиусов за счет уменьшения на , и увеличения на ; сумма абсолютных величин этих деформаций должна быть равна :

Относительное тангенциальное удлинение материала на внутренней поверхности наружного цилиндра равно

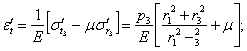
в эту формулу вместо подставлена величина общего для обоих цилиндров радиуса , так как — малая величина и такая замена вводит очень небольшую погрешность. Относительное увеличение радиуса будет тоже ; поэтому

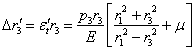
Относительное тангенциальное сжатие материала на наружной поверхности внутренней трубы равно:

укорочение радиуса будет равно:

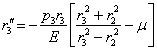
Сумма абсолютных величин и равна по предыдущему

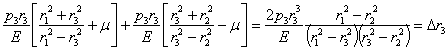
   Таким образом, чтобы обеспечить наличие = принятого нами начального усилия необходимо дать разницу диаметров , равную

   Минимальная температура , до которой надо нагреть наружный цилиндр при надевании его на внутренний, определяется уравнением

(при наших числовых данных : ).

Напряжения в сферических толстостенных сосудах.

   На фиг. 547 изображен элемент, вырезанный из толщи стенки толстостенного сферического сосуда; внутренний радиус этого элемента равен r, а наружный ; напряжения, действующие на этот элемент, изображены на чертеже.

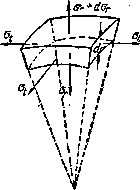Рис.6. фрагмент сферического толстостенного сосуда.

   Составляя уравнения равновесия и совместности, получаем для и значения:

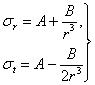
Постоянные А и В могут быть определены из условий на внутренней и внешней поверхностях сосуда при

и 

соответственно, где и — наружный и внутренний радиусы.

Так, при действии внешнего и внутреннего давлений А и В определяются из условий:

на внутренней поверхности,

на внешней поверхности

Отсюда

Тогда

§ 2.16. РАСЧЕТ ТОЛСТОСТЕННЫХ ЦИЛИНДРОВ

Толстостенным называется такой цилиндр, для которого отношение толщины стенки к внутреннему диаметру не менее 1/20.

Рассмотрим задачу о расчете толстостенного цилиндра, подвергающегося действию равномерно распределенных наружного давления  и внутреннего давления  (рис. 3.16, а). Такая нагрузка не может вызывать деформации изгиба цилиндра.

При расчете толстостенных цилиндров нормальные напряжения  в сечениях плоскостями, проходящими через ось О симметрии (см. рис. 3.16, а), нельзя считать равномерно распределенными по толщине стенки, как это делается при расчете тонкостенных цилиндров.

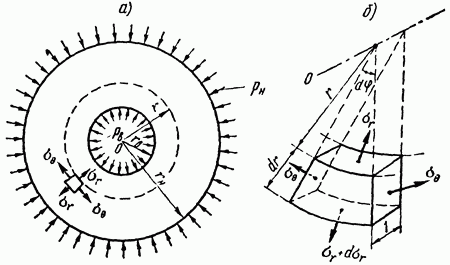
Рис. 3.16

Нормальные напряжения  действующие по цилиндрической поверхности с радиусом  (см. рис. 3.16, а), могут быть того же порядка и даже превышать величины напряжений что при тонкостенных цилиндрах невозможно. Поэтому расчет толстостенных цилиндров нельзя производить по формуле (1.16), применяемой при расчете тонкостенных осесимметричных оболочек.

В связи с полярной симметрией цилиндра и нагрузки нормальные напряжения  и  являются главными напряжениями; в площадках, по которым они действуют, касательные напряжения равны нулю.

Третьим главным напряжением в каждой точке толстостенного цилиндра является напряжение  действующее по площадке, совпадающей с поперечным сечением цилиндра, т. е. с сечением плоскостью, перпендикулярной его оси симметрии.

При выводе расчетных формул рассмотрим открытые цилиндры, т. е. цилиндры, не имеющие днищ. Напряжения  в таких цилиндрах равны нулю.

Точное решение, выполненное методами теории упругости, показывает, что поперечные сечения цилиндра, плоские до его нагружения, остаются плоскими и после нагружения и что, следовательно, относительная деформация  в направлении оси симметрии одинакова во всех точках поперечного сечения. На основании обобщенного закона Гука при 

при 

откуда

Из формулы (3.16) следует, что сумма напряжений о, и  одинакова для всех точек цилиндра.

На рис.  изображен элемент, выделенный из толстостенного цилиндра двумя цилиндрическими поверхностями радиусами , двумя плоскостями, проходящими через ось О симметрии цилиндра и образующими друг с другом угол  и двумя поперечными сечениями, отстоящими друг от друга на расстоянии, равном единице. Все грани элемента совпадают с главными площадками.

Составим условие равновесия элемента в виде суммы проекций действующих на него сил на нормаль к цилиндрическим поверхностям, проведенную через их центры:

Сокращая это выражение на  и пренебрегая бесконечно малыми величинами второго порядка, находим

Заменим в этом уравнении  на  [см. выражение (3.16)]:

или, учитывая, что

получаем

Проинтегрировав последнее уравнение, найдем

где С — постоянная интегрирования.

Постоянные А и С определим из граничных условий на поверхностях цилиндра:

а) на внутренней поверхности цилиндра, т. е. при  и, следовательно,

б) на наружной поверхности цилиндра, т. е. при  и, следовательно,

Решив совместно уравнения (5.16) и (6.16), найдем:

Подставим найденные выражения  и С в уравнение (4.16). После преобразований

После подстановки в уравнение (3.16) выражения 

Равенства (7.16) и (8.16) носят название формул Ламе. В этих формулах расстояние  от точки до оси цилиндра учитывается членами  стоящими в круглых скобках.

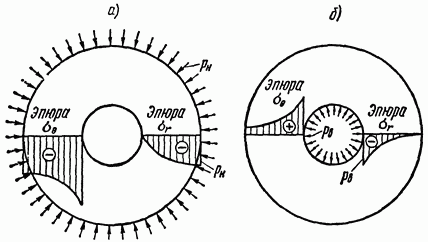
Рис. 4.16

Величины выражений в круглых скобках положительны при любых значениях г.

Следовательно, при действии на цилиндр только наружного или внутреннего давления знаки напряжений  (а также и 09) во всех точках цилиндра одинаковы. В частности, при действии только наружного давления (рис. 4.16, а) напряжения  во всех точках цилиндра отрицательны (сжатие); при действии же только внутреннего давления (рис. 4.16, б) напряжения  во всех точках цилиндра отрицательны (сжатие), а  — положительны (растяжение).