Лабораторная работа № 5. (механика) Определение ускорения свободного падения.

Цель работы:определение ускорения свободного падения в гравитационном поле Земли методом оборотного маятника.

Оборудование: оборотный маятник, математический маятник, секундомер.

Краткая теория.

Колебательным движением, или колебанием, называются процессы или явления, обладающие той или иной степенью повторяемости во времени. Если колебания повторяются через строго определенный промежуток времени, то они называются периодическими, иначе апериодическими. Интервал времени между двумя смежными одинаковыми состояниями колеблющейся системы называется периодом Т:

, (1)

где t – время, за которое совершается N колебаний.

Величина, численно равная числу колебаний, совершаемых колеблющимся телом за единицу времени, называется частотой:

. (2)

В зависимости от типа колеблющейся системы колебания различают механические или электромагнитные, а также их комбинации. Колебания свойственны всем явлениям природы.

Колебания любых физических величин почти всегда связаны с попеременным превращением энергии одного вида в энергию другого вида. Например, колебания груза, подвешенного на нити, можно спровоцировать, задав начальную энергию или отклонением от положения равновесия (сообщением потенциальной энергии), или толкнув маятник (сообщив тем самым кинетическую энергию). Маятник будет совершать колебания, при которых кинетическая и потенциальная энергия будут превращаться друг в друга. Процесс перекачки энергии будет повторяться, пока диссипация (рассеяние) энергии, обусловленное, например, трением, не приведет к полному превращению колебаний.

Колебания бывают следующих видов: гармонические, свободные, затухающие, вынужденные.

Простейшим и наиболее важным типом периодических колебаний является гармоническое колебание. Гармоническими называются колебания, при которых физические величины, описывающие состояние системы, изменяются со временем по синусоидальному или косинусоидальному закону.

При гармонических колебаниях отсутствуют потери энергии, а сами колебания совершаются под действием квазиупругой возвращающей силы (сила, возникающая при отклонении колеблющейся системы от положения устойчивого равновесия и направленная к этому положению). Тогда гармонические колебания описываются следующим уравнением движения (II закон Ньютона):

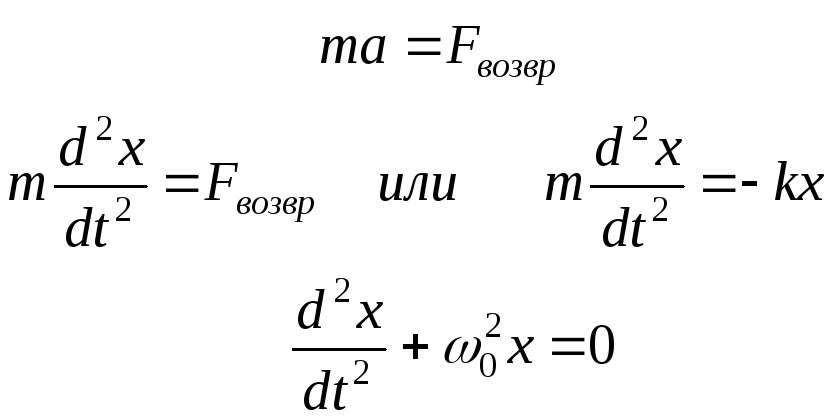, (3)

где - ускорение колеблющейся системы, приобретаемое системой под действием возвращающей силы;

- собственная частота колеблющейся системы массой .

Решение дифференциального уравнения свободных колебаний (3) имеет вид:

, (4)

где х - колеблющаяся величина (например, смещение тела);

А - амплитуда колебаний данной физической величины;

ω₀ - циклическая (угловая) частота колебаний;

φ₀ и φ₁ - начальная фаза колебаний;

φ=(ωt+φ₀) - фаза колебаний.

Уравнение (3) - дифференциальное уравнение гармонических колебаний, а уравнение (4) - решение дифференциального уравнения.

Гармонические колебания незатухающие, это единственный тип колебаний, форма которых не искажается при прохождении через идеальные системы (т.е. через системы в которых отсутствуют силы сопротивления).

Свободные колебания - колебания, которые совершаются при отсутствии внешних воздействий за счет первоначально внесенной энергии (потенциальной или кинетической).

Колебания, зависящие только от параметров системы, называются собственными. Частота этих колебаний называется собственной и обозначается ω₀.

Все реальные свободные колебания являются затухающими. Незатухающие свободные колебания характерны только для идеализированной системы, в которой не действуют силы трения, силы сопротивления среды.

Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии за счет периодического внешнего воздействия. Колебания, возникающие под действием внешней периодически изменяющейся силы, называются вынужденными.

Маятником называется твердое тело, совершающее под действием приложенных сил колебания около неподвижной точки или вокруг оси. Математическим маятником называется идеализированная система из невесомой нерастяжимой нити и материальной точки, совершающая колебания в поле сил тяжести.

Ближе всего по свойствам к математическому маятнику подходит система из очень легкой практически нерастяжимой нити и подвешенного тяжелого груза малых размеров. Центр тяжести такой системы можно считать совпадающим с центром тяжести груза.

К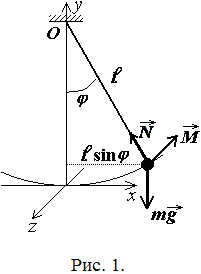огда система находится в покое, сила тяжести уравновешена натяжением нити. Если маятник отклонить от положения равновесия, то результирующая сил тяжестии натяжения нити, будет стремиться вернуть тело в прежнее положение (рис. 1). Так как сила тяжести и сила натяжения нити лежат в одной плоскости, то и колебания маятника будут происходить в той же самой плоскости.

Будем характеризовать отклонение маятника от положения равновесия углом , образованным нитью с вертикалью. Отклонение маятника приводит к возникновению возвращающего момента силы тяжести:

, (5)

где - модуль силы тяжести;

- плечо силы тяжести.

Знак минус в (5) указывает на то, что момент силы тяжести направлен так, что стремится вернуть маятник в положение равновесия.

Запишем уравнение движения маятника. Основное уравнение динамики вращательного движения имеет вид:

, (6)

где - момент инерции маятника относительно оси вращения;

- угловое ускорение.

Таким образом, получаем:

.

Это уравнение можно привести к виду:

. (7)

Рассмотрим малые колебания маятника. При таких колебаниях () можно считать, что. Введем, кроме этого, обозначение

. (8)

Итак, окончательно, получаем уравнение

. (9)

Получено уравнение типа (3). Следовательно, уравнение (9) - это дифференциальное уравнение гармонических колебаний математического маятника. Решением этого уравнения является уравнение вида (4), т.е.:

. (10)

Формула (10) означает, что при малых колебаниях математического маятника около положения устойчивого равновесия, угловое смещение маятника изменяется по гармоническому закону (при отсутствии сил сопротивления).

Зная (8), можно найти период колебаний маятника:

. (11)

Величина , определяемая соотношением (8), называетсясобственной частотой колебаний маятника. Эта величина, также как и период, зависит только от длины нити и ускорения свободного падения, и не зависит ни от массы груза, подвешенного на нити, ни от амплитуды колебаний. Поэтому наблюдения за колебаниями маятника используются для определения ускорения свободного падения . Такие наблюдения имеют большое значение для изучения геологической структуры земной коры в верхних ее слоях. Наличие под землей залежей руды или нефти влияет на численное значение ускорения свободного падения. Поэтому маятники применяют при геологических разведках этих ископаемых.

Физический маятник – это твердое тело, которое может совершать свободные колебания под действием силы тяжести относительно оси, не проходящей через центр масс. В положении устойчивого равновесия центр масс С находится на одной вертикали с точкой подвеса маятника О. При отклонении маятника на некоторый угол φ возникает вращательный момент - момент силы тяжести, стремящийся вернуть маятник в положение равновесия:

, (12)

здесь - масса маятника;- расстояние между точкой подвеса и центром масс маятника. Знак "минус" в формуле (12) имеет тот же смысл, что и в формуле (5).

Запишем теперь уравнение моментов, полагая, что трение на оси отсутствует:

, (13)

где - момент инерции маятника относительно точкиО.

Ограничимся случаем малых колебаний (т.е. ). тогда:

. (14)

Очевидно, что это уравнение аналогично уравнениям (7) и (9). Введем следующее обозначение:

. (15)

Таким образом, получаем уравнение идентичное (9):

. (16)

Уравнение (16) - дифференциальное уравнение гармонических колебаний физического маятника. Решением уравнения (16) является уравнение вида (4), т.е.:

. (17)

Колебания совершаются с собственной частотой, равной:

и периодом

. (18)

Период колебаний физического маятника тем больше, чем больше его момент инерции и чем меньше расстояние от оси до его центра тяжести.

Сравнивая выражения (11) и (18), можно придти к выводу, что физический маятник колеблется с тем же периодом, что и математический, имеющий длину

, (19)

называемой приведенной длиной данного физического маятника. Приведенная длина - это длина такого математического маятника, который с данным физическим маятником имеет одинаковый период колебания. Т.е.:

. (20)

Если l_пр отложить от точки подвеса по прямой, проходящей через точку подвеса и центр масс С, то получится точка О¢ (см. рис. 2), называемая центром качания. Центр качания обладает одним замечательным свойством: при подвешивании маятника в точке О¢ приведенная длина l_пр и период Т₀ получатся теми же, что и при подвешивании в точке О.