General Physics - Thermodinamics archive / ошибки измерений (макет)

Министерство образования Российской Федерации Омский государственный университет

Обработка результатов измерения физических величин

Лабораторный практикум (для студентов физического факультета,

специальность 010400 «Физика»)

1

Обработка результатов измерения физических величин.

Измерением называется определение значения физической величины опытным путем. Значение величины, найденное таким способом, называется результатом измерения. Измерения классифицируются на прямые и косвенные.

Прямым называется измерение, при котором искомое значение величины находится непосредственно из опыта путем отсчета по шкале измерительного прибора, например: измерение длины линейкой, определение температуры тела термометром и т. д.

Косвенным называется измерение, при котором искомое значение величины находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям, например: определение плотности тела по его геометрическим размерам и массе, определение силы тока по напряжению и сопротивлению и т. д.

Как известно, никакое измерение не может быть выполнено абсолютно точно, поэтому результат измере-

ния в той или иной мере отклоняется от истинного значения измеряемой величины. Разница между результатом измерения и истинным значением измеряемой величины называется абсолютной погрешностью измерения и определяется формулой:

xi = xi – X,

где Х – истинное значение измеряемой величины, хi – результат i-того измерения, xi – абсолютная погрешность i- того измерения.

Наряду с абсолютной погрешностью, используется относительная погрешность равная отношению абсолютной погрешности к истинному значению измеряемой величины:

i xi / X.

3

Существует три типа погрешностей: систематические, случайные и промахи.

Систематическими называются погрешности, величина которых не меняется при повторении измерений данной величины при тех же способах измерения. Систематические погрешности возникают в тех случаях, когда не учитывается влияние на результаты эксперимента различных постоянно действующих факторов, например: температуры, давления, сопротивления подводящих проводов и т.д. Источником систематических погрешностей может быть также неточность градуировки измерительного прибора или его неисправность.

Случайными называются погрешности, величина и знак которых меняется непредсказуемым образом при повторных измерениях данной величины в тех же условиях. Источником случайных ошибок может быть и сам экспериментатор из-за несовершенства органов его чувств. Так, например, результаты повторных измерений периода колебаний математического маятника с помощью очень точного секундомера обязательно окажутся несколько отличными друг от друга вследствие того, что моменты нахождения маятника в соответствующих фазах отклонения фиксируются неточно: при пуске секундомера экспериментатор может несколько замешкаться, при его остановке, или, наоборот, поспешить. Случайные погрешности отклоняют результат то в одну, то в другую сторону от истинного значения измеряемой величины, поэтому результаты большого числа измерений симметрично располагаются относительно Х.

метическим результатом серии измерений. Так как при большом числе измерений величина x очень мала, то можно считать, что x X . Чем больше n, тем точнее выполняется это равенство.

4

Промах – это грубая погрешность, вызванная невнимательностью экспериментатора (неверный отсчет показаний прибора, описка при записи показаний и т. д.). Промахи могут сильно исказить результаты измерений, особенно в тех случаях, когда их число невелико. Их следует исключать из результатов измерений.

Нормальный закон распределения случайных погрешностей.

Если погрешности носят чисто случайный характер, то по результатам измерений можно оценить вероятности их появления. Пусть х1, х2…хn – результаты отдельных измерений. Примем, что n достаточно велико, и при оценке погрешностей будем считать, что

X x 1 n xi , n i 1

(1)

xi xi x.

Определив погрешности xi, рассортируем их по величине. Для этого весь диапазон полученных значений xi разобьем на малые одинаковые интервалы и подсчитаем, сколько раз величина ошибки попадает в каждый интервал. Если в интервале номер «k» оказалось заключеноnk значений погрешности, то вероятность попадания погрешности в этот интервал

стей соответствует так называемому нормальному закону, найденному Гауссом. Согласно гауссову распределению, плотность вероятности y и величина погрешности xi связаны соотношением:

5

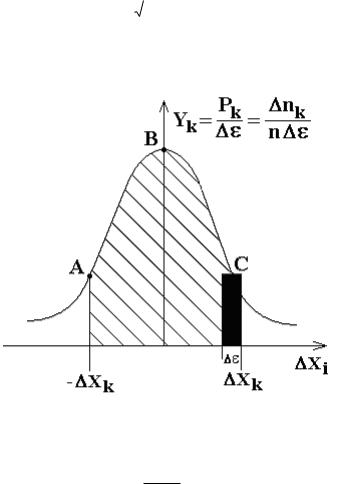
дисперсией распределения. Вид кривой распределения, соответствующий некоторому значению , показан на рис. 1.

Рис. 1. Кривая распределения Гаусса вероятности случайных погрешностей.

P( xk) того, что величина погрешности заключена в интер-

вале xk xk + , определяется формулой:

P( xk) = y( xk)· .

Численно эта вероятность равна площади черного прямоугольника под точкой С с основанием (см. рис. 1). Веро-

6

ятность того, что модуль погрешности не превзойдет некоторого значения, изобразится площадью заштрихованной фигуры АВС с основанием 2 xk.

На рисунке 2 представлены кривые распределения, соответствующие разным . Как видно, с ростом максимум кривой распределения понижается, а ее «крылья» поднимаются. Это означает, что с ростом вероятность малых погрешностей уменьшается, а вероятность больших – растет. Следовательно, чем больше дисперсия распределения2, тем меньше точность измерений.

Рис. 2. Влияние дисперсии на вид кривой распределения вероятностей случайных погрешностей.

Следует отметить, что кривая y( xi) характеризует не конечную серию измерений, а совокупность бесконечного числа измерений данной величины в одних и тех же условиях.

7

Среднеквадратичная погрешность.

Пусть х1, х2…хn – результаты некоторой серии n измерений, проведенных в одинаковых условиях. Как уже подчеркивалось, величина случайной погрешности не постоянна и меняется от опыта к опыту. Возникает необходимость охарактеризовать погрешности результатов отдельных измерений данной серии некоторой средней величиной. Иногда в качестве такой характеристики используют среднюю арифметическую погрешность:

x 1 n xi . n i 1

Однако удобнее использовать так называемую

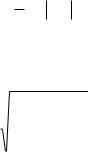
среднеквадратичную погрешность выборки Sn, опреде-

ляемую формулой:

Можно показать, что при достаточно большом числе измерений Sn σ и, следовательно, дисперсия распределения

Таким образом, дисперсия распределения приблизительно равна среднему квадрату погрешности отдельных измерений, найденному при достаточно большом числе n. Для генеральной совокупности (n → ∞) равенство (5) выполняется точно. Из него следует, что величина дисперсии зависит от условий, в которых проводятся измерения: чем благоприятнее условия измерений, тем меньше разброс результатов и меньше дисперсия.

8

Среднеквадратичная погрешность среднего.

Допустим, что мы провели серию n измерений некоторой величины х, результаты которых равны х1, х2,…хn. Наилучшим приближением к истинному значению является величина

x 1 n xi , n i 1

называемая средним выборочным значением измеряемой величины. Если серию по n измерений в каждой повторить m раз, то мы получим m значений x , несколько отличающихся друг от друга и от истинного значения Х измеряемой величины. Погрешности xk xk X являются слу-

чайными и так же, как погрешности отдельных измерений xi = xi – Х, подчиняются гауссову распределению, но с

другой дисперсией x2 < 2 . Величина x2 , называемая

дисперсией среднего, является мерой погрешности среднего значения x , найденного в серии из n измерений. В теории погрешности доказывается, что

Таким образом, среднеквадратичная погрешность среднего результата n измерений в n1/2 раз меньше среднеквадратичной погрешности отдельных измерений.

Доверительный интервал и доверительная вероятность.

Как уже указывалось, для любой конечной выборки x ≠Х. Практически очень важно оценить возможную величину отклонения среднего значения x от истинного Х, то есть, x –Х. Интервал x Х, в который с заданной вероятностью α попадает истинное значение Х измеряемой величины, называется доверительным интервалом, соответст-

9

вующим вероятности α. Вероятность α называется также

доверительной вероятностью или надежностью. Вели-

чина Х характеризует точность оценки. Чем меньше разность x –Х, тем выше точность.

Надежность, соответствующую заданной точности Х, можно вычислить теоретически, воспользовавшись га-

уссовым распределением, если известна дисперсия x2 . Так как x2 σ2/n, то надежность, соответствующая заданной

точности Х, растет с ростом числа измерений и величины дополнительного интервала. Если n мало, то используют распределение, выведенное Госсетом (псевдоним «Стьюдент»).

В распределении Стьюдента плотность распределения вероятностей рассматривается как функция величины

Распределение Стьюдента зависит от n и при n→∞ переходит в распределение Гаусса.

Вычислив по результатам измерений S x и задав ве-

личину X, можно найти t и α, соответствующие данному n. Или, наоборот, задав надежность α, можно вычислить tα,n и соответствующую точность X = tα,n· S x при данном зна-

чении n. Соответствующие друг другу значения α и tα,n при разных n приводятся в специальных таблицах (см. Приложение 1). На практике задание величины X определяется конкретными условиями. В лабораторных условиях обычно довольствуются надежностью α = 0,90; 0,95.

Для оценки доверительного интервала прямых измерений предлагается следующий порядок:

1.Провести серию измерений изучаемой величины Х и оценить среднее выборочное x по формуле:

x1 n xi . n i 1

10