Министерство Образования Российской Федерации

Новосибирский Государственный Технический Университет

Кафедра Прикладной Математики

Задание по Геометрии и алгебре на тему «Линейные пространства и СЛАУ»

Факультет: ПМИ

Группа: ПМ-22

Студент: Рембиш А.В.

Вариант: 21

Преподаватель: Чубич В.М.

Новосибирск 2002

Задания

Цель задания: ознакомление с понятиями ортогонального дополнения, проекции вектора на подпространство, орта вектора к подпространству, ортогональной системы векторов и процедурой ортогонализации Грамма-Шмидта.

Срок выполнения: две недели.

Время защиты: по указанию преподавателя.

Содержание задания

Задача 1. Найдите все базы каждой из двух систем векторов. Определите, эквивалентны ли эти системы. Для каждой из систем векторов найдите такую базу, чтобы линейно-зависимые векторы системы выражались через векторы базы в виде линейной комбинации с целыми коэффициентами. Запишите соответствующие выражения.

Задача 2. Выполните ортогонализацию базиса двумерного подпространства L, заданного одной из систем векторов в задачах 1 или 2 задания 2, и дополните его до ортогонального базиса пространства R₄.

Дано

Задача 1:

Задача 2:

Задача 3:

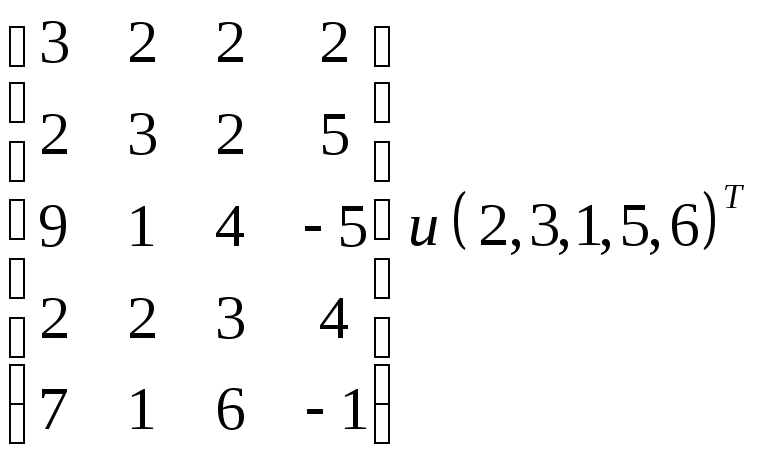
Задание 1

Найдем размерность первой системы векторов – x_i, i = 1, 2, 3, 4:

Получаем, что у данной системы векторов может быть до четырех баз, каждая из которых состоит из трех векторов начальной системы. Найдем те векторы, которые будут являться базами данной системы:

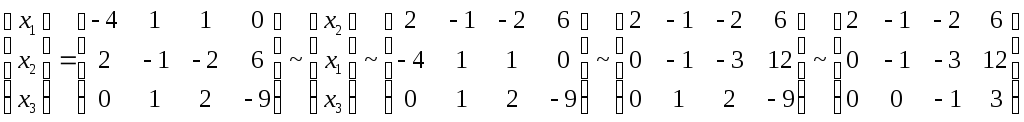
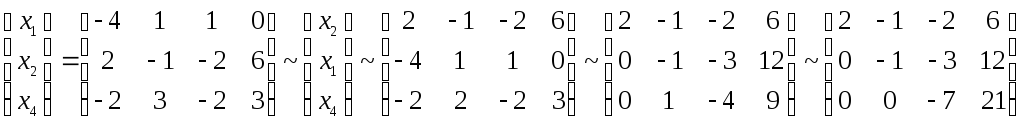
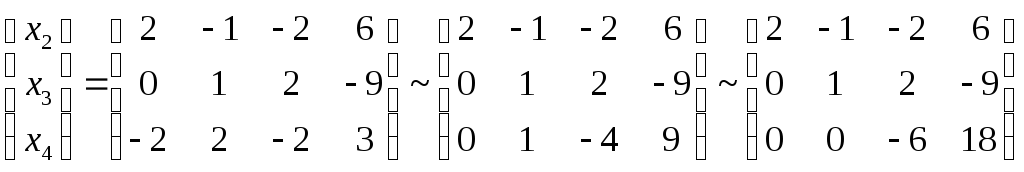
Получили, что базами системы векторов L₁ являются подсистемы .

Проделаем теперь те же действия и для второй системы векторов:

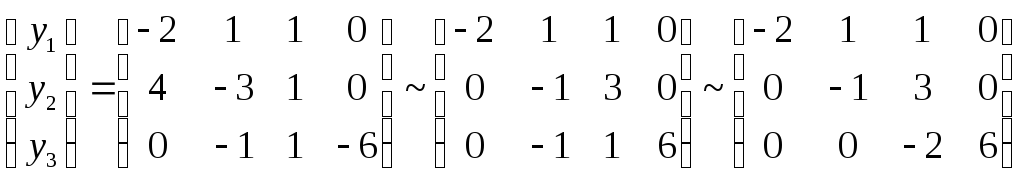
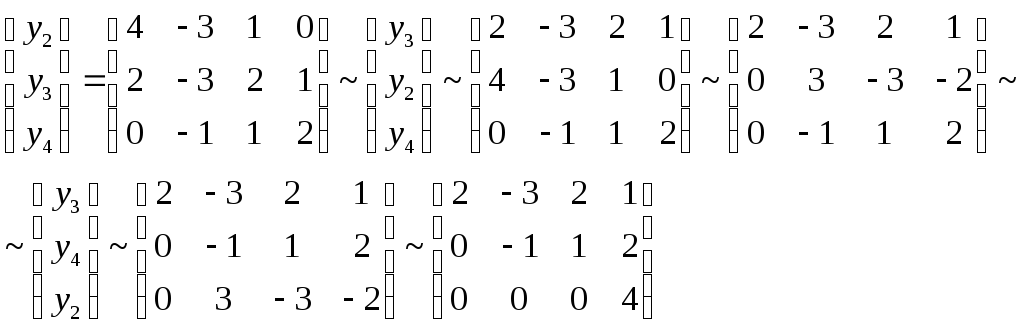
Так же как и в первом случае получаем, что все возможные подсистемы, состоящие из трех векторов, являются базами.

Так как ранги заданных систем векторов совпадают, то системы могут быть эквивалентными. Поэтому проверим их на эквивалентность:

Получили, что ранг объединенной системы векторов не равен рангам начальных систем векторов, и, как следствие, данные системы не эквивалентны.

Теперь выразим линейно зависимые векторы обеих систем через векторы одной из баз:

• ;

• .

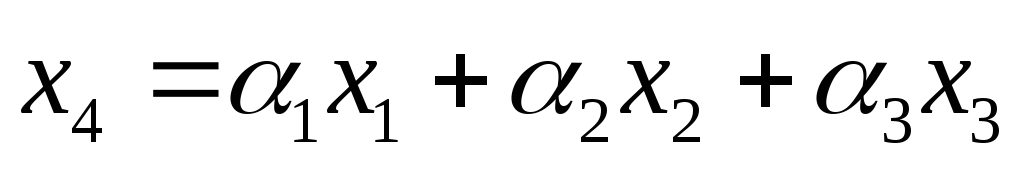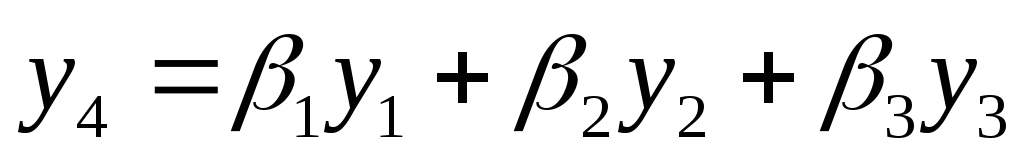Для этого составим и решим две системы уравнений:

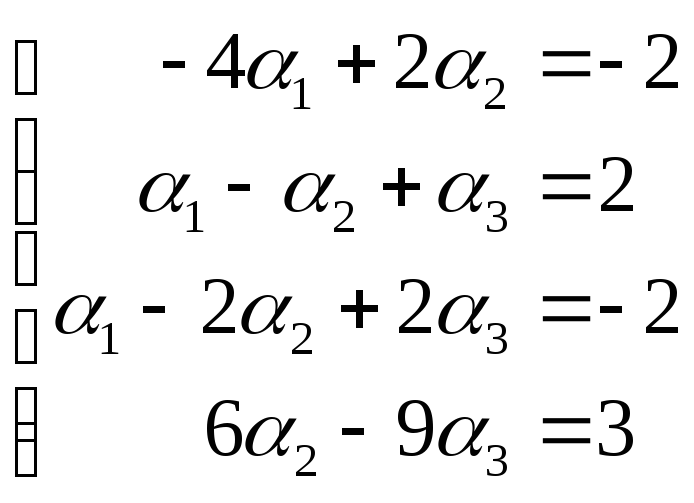
Из системы получаем:

Теперь сделаем проверку полученного результата. Т.к. , то, подставив в это уравнение полученные величины, мы должны получить верное равенство:

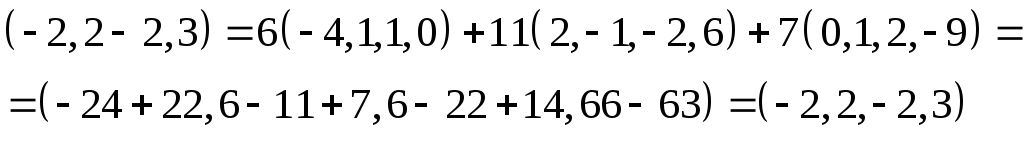
Теперь проделаем то же самое и для второго уравнения:

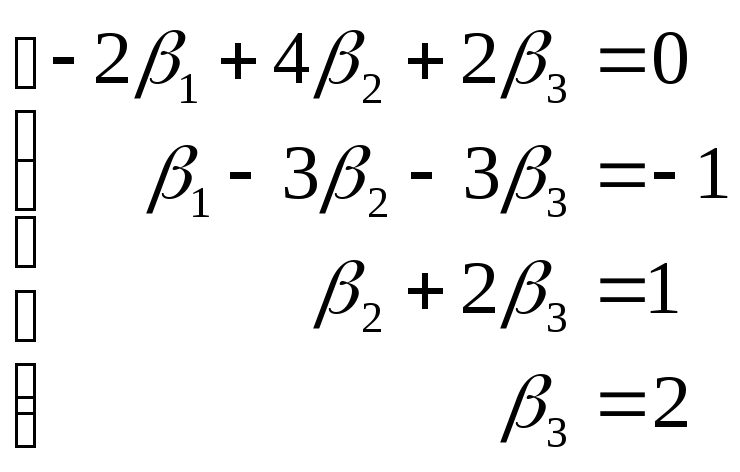
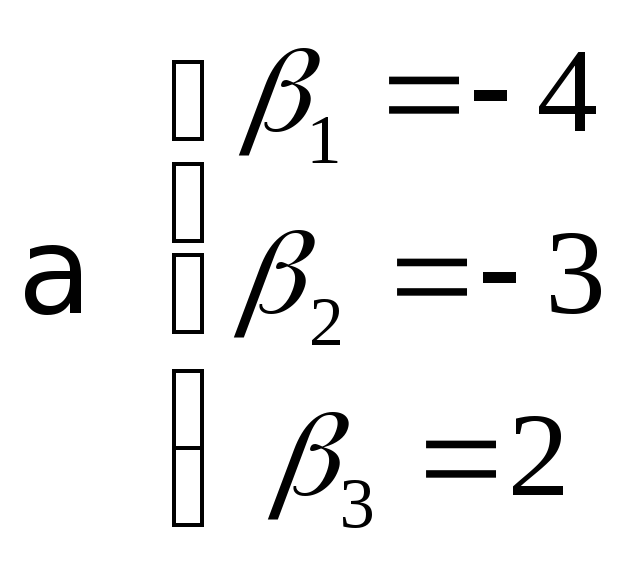
И, наконец, проверка:

Задание 2

Найдем размерность подпространства L₁, порожденного векторами x_i, i = 1,2,3,4:

Найдем размерность подпространства L₂, порожденного векторами y_i, i = 1,2,3,4

Теперь найдем ранг объединенной системы векторов, в которую войдут все линейно независимые векторы обоих подпространств:

Теперь из формулы получаем, что ранг пересечения данных подпространств равен 2.

Обозначим базисные вектора пересечения подпространств через z₁ и z₂. По определению пересечения подпространств:

или

Слева от равенства записаны векторы, вошедшие в базис суммы подпространств. Для векторов, стоящих справа от знака равенства, выберем значения в соответствие с таблицей:

i	1i	2i
1	1	0
2	0	1

Теперь запишем полученные системы и решим их методом Гаусса:

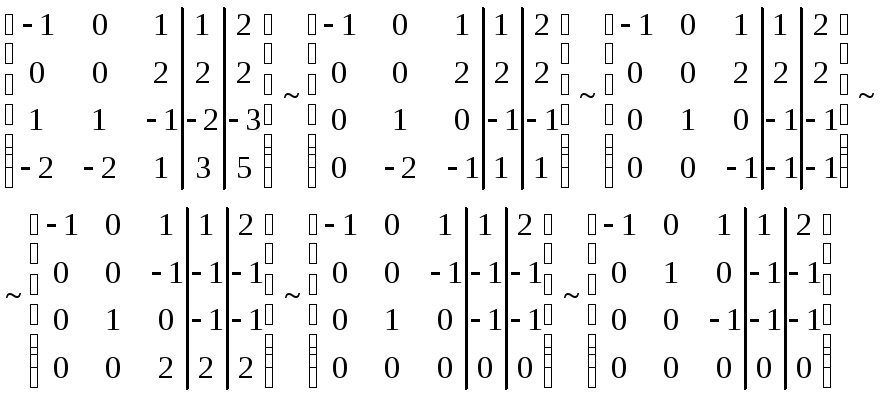
Теперь найдем коэффициенты:

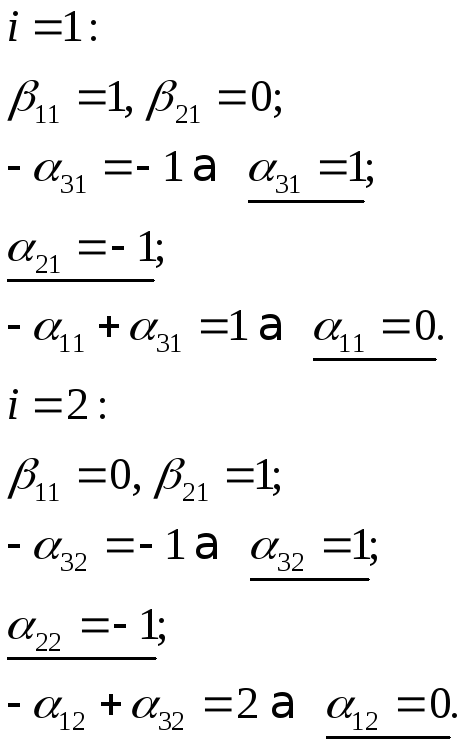
Теперь проверим полученные результаты:

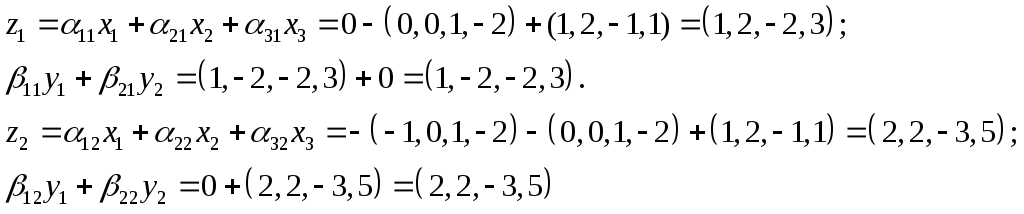
Задание 3

Решим данную СЛАУ с помощью расширенной матрицы:

Т.к. , то данная СЛАУ является совместной. В силу того, что , то получаем, что система имеет одну свободную переменную. Пусть ею будет x₄. Тогда:

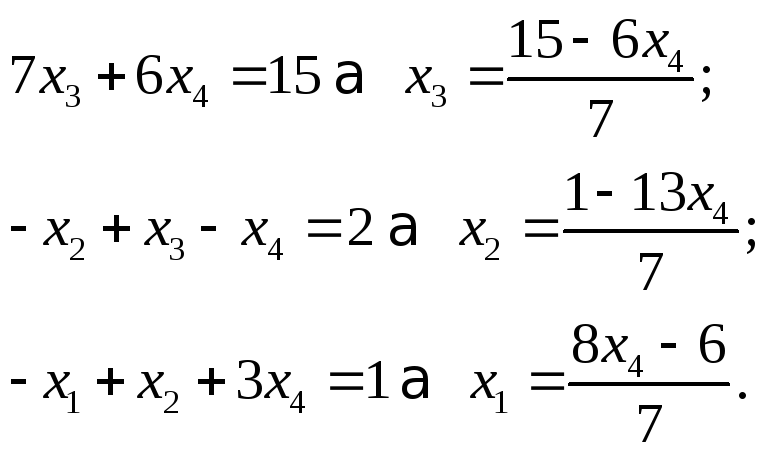
Следовательно, общее решение неоднородной СЛАУ:

Проверим полученное решение:

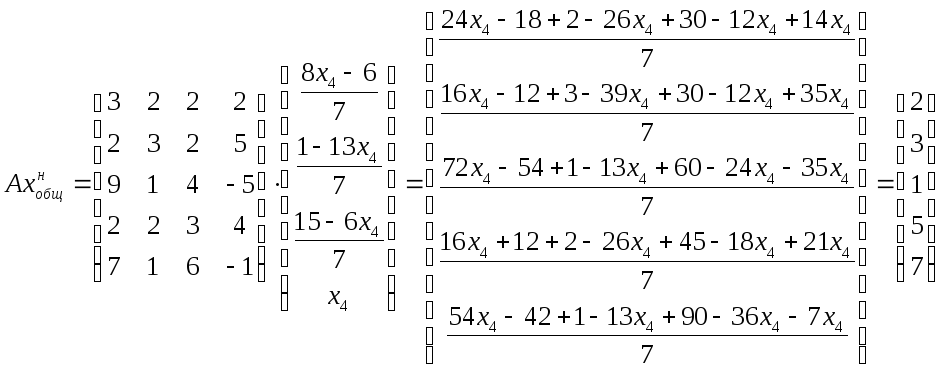
Т.к. мы знаем, что , то получаем:

Т.е. частное решение неоднородной СЛАУ: , а вектор образует фундаментальную систему решений соответствующей однородной СЛАУ.