Практика 36. Выпуклость функции, точки перегиба, асимптоты

36.1.Выпуклость функции

Определение 36.1. Функция f(x) называется в ы п у к л о й или в ы - п у к л о й в н и з на интервале (a; b), если для любых точек x1; x2 2(a; b)

и любой точки x 2 (x1; x2) выполняется неравенство f(x) l(x); где l(x) = )(x2 x) функция, задающая прямую, проходящую

через точки (x1; f(x1)) è (x2; f(x2)), то есть все точки графика f, соответствующие x 2 (x1; x2), расположены ниже отрезка с концами в точках (x1; f(x1)) è (x2; f(x2)), или на этом отрезке.

Определение 36.2. Функция f(x) называется в о г н у т о й или в ы - п у к л о й в в е р х на интервале (a; b), если для любых точек x1; x2 2 (a; b) и любой точки x 2 (x1; x2) выполняется неравенство f(x) l(x); то есть все точки графика f, соответствующие x 2 (x1; x2), расположены выше отрезка с концами в точках (x1; f(x1)) è (x2; f(x2)), или на этом отрезке.

Определение 36.3. Функция f(x) называется с т р о г о в ы п у к л о й в н и з (с т р о г о в ы п у к л о й в в е р х) на интервале (a; b), если для любых точек x1; x2 2 (a; b) и любой точки x 2 (x1; x2) выполняется неравенство f(x) < l(x) (f(x) > l(x)):

Всякий интервал на котором функция (строго) выпукла вверх (вниз) называется интервалом (строгой) выпуклости вверх (вниз) для этой функции.

Теорема 36.1.1 (Достаточное условие выпуклости) . Åñëè f00(x) > 0 (f00(x) < 0) для всех x 2 (a; b), то функция f(x) строго выпукла вниз (вверх) на этом интервале.

Пример 36.1 ( 1307). Исследовать выпуклость функции f(x) = xx; ãäå x > 0.

Поскольку вторая производная этой функции

то по достаточному условию выпуклости в данной области функция строго выпукла вниз.

1

36.2.Точки перегиба

Определение 36.5. Пусть функция f дифференцируема при x = x0 è пусть y = L(x) f(x0)+f0(x0)(x x0) уравнение касательной к графи-

ку функции f в точке (x0; f(x0)). Если разность f(x) L(x) меняет знак при переходе через точку x0, òî x0 называется точкой перегиба функции f, точка (x0; f(x0)) называется точкой перегиба графика функции.

Точку x0, в которой функция f дифференцируема, назовем в о з м о ж н о й т о ч к о й п е р е г и б а, если f00(x0) = 0 или не существует f00(x0).

Теорема 36.2.1 (Первое достаточное условие точки перегиба) . Если функция f(x) дифференцируема в точке x0, дважды дифференцируема в

некоторой проколотой окрестности U0(x0) этой точки и вторая производная f00(x) меняет знак при переходе через точку x0, òî x0 является

точкой перегиба функции f.

Пример 36.2 ( 1301). Найти промежутки выпуклости, вогнутости и точки перегиба графика функции y = x + x5=3.

Найдем вторую производную заданной функции:

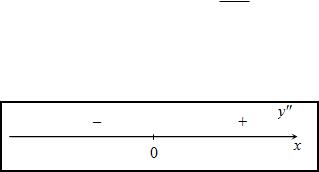
Функция всюду дифференцируема, вторая производная не существует в точке x = 0. Знак второй производной: y00(x) > 0 ïðè x > 0, y00(x) < 0

ïðè x < 0.

Ðèñ. 1: Çíàê x + x5=3 00.

Так как на полупрямой (0; +1) вторая производная y00(x) > 0, òî

на этом промежутке функция выпукла; в силу того, что на полупрямой (1; 0) вторая производная y00(x) < 0 функция вогнута. Так как при

переходе через точку x = 0 вторая производная меяет знак, то эта точ- ка является точкой перегиба функции. Соответственно, (0; 0) точка перегиба графика функции.

2

36.3.Асимптоты графика функции

èëè 1.

Замечание 36.1. Прямая x = a не может быть вертикальной асимптотой, если функция непрерывна в точке x = a. Поэтому вертикальные асимп-

тоты следует искать в точках разрыва функции или на границе области определения.

Определение 36.8. Пусть функция f определена на бесконечном интервале (a; +1). Говорят, что прямая l(x) = kx + b является н а к л о н - н о й а с и м п т о т о й графика функции y = f(x) при x ! +1, если

Теорема 36.3.1 (Критерий наклонной асимптоты). Для того чтобы график функции f(x) имел при x ! +1 наклонную асимптоту y =

kx + b, необходимо и достаточно, чтобы существовали два предельных значения

Замечание 36.2. При k = 0 наклонную асимптоту называют г о р и з о н - т а л ь н о й.

Следствие 36.3.2. Для того чтобы график функции f(x) имел при x ! +1 горизонтальную асимптоту y = b, необходимо и достаточно,

чтобы

lim f(x) = b:

x!+1

Замечание 36.3. Для случая x ! 1 аналогично определяется наклонная асимптота, формулируется критерий и следствие.

Пример 36.3 ( 1492). Найти асимптоты графика функции

p

x2 x2 1 y = 2x2 1 :

Область определения функции X = fx 2 R : jxj 1:g

3

Заметим, что знаменатель в области определения не обращается в ноль, следовательно, функция не имеет точек разрыва на множестве X.

Поэтому вертикальных асимптот нет.

Проверим наличие горизонтальных асимптот. Так как

то горизонтальных асимптот нет, но могут быть наклонные. Действительно,

Следовательно, y = x=2 наклонная касательная графика функции при x ! +1. Теперь, проверим наклонную асимптоту при x ! 1.

Следовательно, y = x=2 наклонная касательная графика функции при x ! 1.

Можно было заметить с самого начала, что f( x) = f(x), и написать уравнение касательной при x ! 1, исходя из симметрии графика относительно оси Oy.

4