Лабораторная работа №12 градуировка шкалы частот генератора переменного напряжения

Цель работы — градуировка шкалы частот генератора переменного напряжения методом биений и методом фигур Лиссажу.

Приборы и принадлежности: два генератора переменного напряжения звуковой частоты, электронный осциллограф, панель для присоединения генераторов и осциллографа.

Краткие сведения из теории

Биениями называются периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний одного направления с близкими частотами. Пусть амплитуды колебаний а₁=а₂=а, частоты  и  +  ( << ). Из уравнений колебаний

y₁=аcost и y₂=аcos(+)t (12.1)

видно, что разность фаз складываемых колебаний все время изменяется так, что колебания оказываются в какой-то момент времени синфазными, через некоторое время — в противофазе и т. д. В зависимости от разности фаз, ампли­туда А результирующего колебания периодически достигает то наибольшего значения A= a₁ + a₂=2a, то наименьшего А=а₁ – а₂ = 0 (рис. 12.1).

Это и есть биения. Уравнение биений можно получить, сло­жив уравнения (12.1):

.

Рис. 12.1

Во втором множителе можно пренебречь членом /2 по сравнению с , так как  << , и рассматривать полученное уравнение как уравнение гармонического колебания с час­тотой  и переменной, медленно изменяющейся амплитудой. Амплитуда биений определяется модулем первого мно­жителя:

.

Частота изменений амплитуды называется частотой биений

_б==|₂ – ₁|. (12.2)

Период изменения амплитуды называется периодом биений: Т_б=1/_б. Метод биений широко применяется на практике для сравнения измеряемой и эталонной частот.

Фигурами Лиссажу называются замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Вид фигур Лиссажу зависит от соотношения между частотами, фазами и амплитудами обоих колебаний. Пусть уравнение взаимно перпендикулярных колебаний вдоль х и у имеют вид:

х = а_хcos(t+₁), у = а_уcos(t+₂).

Частоты этих колебаний равны: _х=_у==2, а начальные фазы ₁ и ₂ различны.

Исключив из уравнений взаимно перпендикулярных коле­баний время t, получим уравнение траектории движения точки, участвующей в обоих колебаниях:

, (12.3)

где  = ₂ – ₁ – разность фаз колебаний.

Полученное уравнение есть уравнение эллипса, оси кото­рого ориентированы произвольно относительно координатных осей хиу. Этот эллипс вписывается в прямоугольник со сторонами 2а_х и 2а_у. Исследуем форму траектории в неко­торых частных случаях, в зависимости от разности начальных фаз .

1. Разность фаз  = ₂ – ₁ = 2n, где n = 0, ±1, ±2 .... В этом случае уравнение (12.3) приводится к виду х/а_х–у/а_у=0, откуда получается уравнение прямой у=(а_у/а_х)х, проходящей через начало координат и расположенной в пер­вом и третьем квадрантах (см. рис. 12.2).

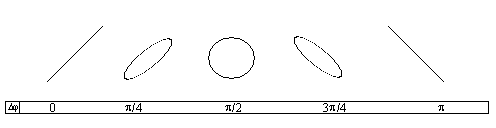
_х : _у= 1 : 1

Рис. 12.2

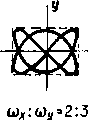
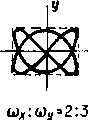
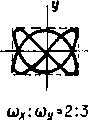
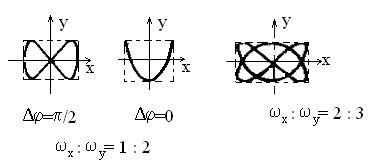
2. Разность фаз  = (2n+1), где n = 0, ±1, ±2, ±3 ...

В этом случае уравнение (12.3) приводится к виду х/а_х + у/а_у =0, откуда следует, что результирующее движе­ние точки представляет собой колебание вдоль прямой у= – (а_у/а_х)х, проходящей через начало координат и расположенной во втором и четвертом квадрантах.

3. Разность фаз =(2n+1)/2, где n = 0, ±1, ±2 .... Уравнение (12.3) может быть представлено в виде . Это уравнение эллипса, приведенного к осям координат (рис. 12.2), причем полуоси эллипса равны соот­ветствующим амплитудам колебаний. При равенстве ампли­туд a_x=a_y=R эллипс вырождается в окружность радиуса R и уравнение принимает вид х²+ y² = R².

Если частоты взаимно перпендикулярных колебаний точно не совпадают, а отличаются на малую величину , то уравнения колебаний можно записать:

х = а_хcos(t+₁), у = а_уcos[t+(t+₂)].

Выражение (t+₂) – ₁ можно рассматривать как раз­ность фаз этих колебаний, медленно изменяющуюся со вре­менем. Вследствие изменения разности фаз эллипс будет непрерывно деформироваться, что мы и наблюдаем при выполнении работы.

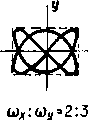
При различных частотах колебаний вдоль осей хиу(_х  _у ) траектории результирующего движения имеют вид довольно сложных кривых. При существенно различных частотах замкнутые кривые не наблюдаются, однако, если частоты колебаний относятся как небольшие целые числа m и n: _х/_у=_х/_у=m/n, то движущаяся точка периодически возвращается в исходное положение. При заданном отношении частот взаимно перпендикулярных колебаний форма фигуры Лиссажу

Фигуры Т_х/Т_у = _х/_у Лиссажу характеризуются следующими свойст­вами. Они вписываются в прямоугольник со сторонами 2а_х и 2а_у. Отношение числа касаний фигурой Лиссажу сторон прямоугольника, в который она вписывается, равно отноше­нию периодов колебаний или обратно отношению частот: N_х/N_y Т_х/Т_у=_х/_у. При заданном отношении частот взаимно перпендикулярных колебаний форма фигуры Лиссажу зависит от разности их фаз (рис. 12.2). Фигуры Лиссажу можно наблюдать на экране электронного осциллографа. Метод фигур Лиссажу — удобный метод исследования соот­ношений между частотами и фазами колебаний.