
- •Методические указания
- •Луганск 2002
- •Методические указания
- •Луганск 2002
- •I. Дифференциальное исчисление функций нескольких переменных
- •II. Неопределенный интеграл
- •1.Интегралы от функций, содержащих квадратный трехчлен
- •2. Интегрирование рациональных дробей
- •3.Интегрирование по частям
- •4. Интегрирование некоторых тригонометрических функций
- •5. Интегрирование некоторых иррациональных функций
- •4. Некоторые геометрические положения определенных интегралов
- •5. Несобственные интегралы
- •IV. Обыкновенные дифференциальные уравнения и их системы
- •Контрольная работа №4 Найти неопределенные интегралы
- •Контрольная работа №5
- •131. .
- •281. 282.
- •Методические указания
- •91034,Г. Луганск,кв Молодежный, 20а
IV. Обыкновенные дифференциальные уравнения и их системы
Дифференциальное уравнение
![]() называется однородным, если функция
называется однородным, если функция![]() зависит от отношения переменных
зависит от отношения переменных![]() (или
(или![]() ).
В этом случае надо ввести новую переменную
).
В этом случае надо ввести новую переменную![]() (или
(или![]() ),
отсюда
),
отсюда![]() .
Уравнение
.
Уравнение![]() примет вид
примет вид![]() ,
и переменные легко разделяются.
,
и переменные легко разделяются.
![]()
Интегрируя, находим решение уравнения.
В задачах №№ 201-210 все дифференциальные
уравнения однородные, т.к. легко получить
отношение переменных
![]() тем или иным способом, а именно, если
тем или иным способом, а именно, если![]() ,
то выносим
,
то выносим![]() в числителе и знаменателе за скобку, а
затем сократим на
в числителе и знаменателе за скобку, а
затем сократим на![]() ,
или выделим
,
или выделим![]() как функцию от
как функцию от![]() и
и![]() .
.
Пример 1. Найти общее решение дифференциального уравнения
![]() .
.
Решение. Выделим
![]() как функцию
как функцию![]() .
Для этого
.
Для этого![]() перенесем в правую часть уравнения с
обратным знаком, а затем это уравнение
разделим на
перенесем в правую часть уравнения с
обратным знаком, а затем это уравнение
разделим на![]()
![]() ,
получим
,
получим
![]() .
.
Замена
![]() ,
отсюда
,
отсюда![]() и
и![]() .
.
Подставив
![]() и
и![]() в уравнение, получим дифференциальное
уравнение с разделяющими переменными
в уравнение, получим дифференциальное
уравнение с разделяющими переменными
![]() или
или![]() ,
или
,
или![]() .
.
Так как
![]() ,
то
,
то![]() .
.
Разделив переменные
![]() и проинтегрировав
и проинтегрировав![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
получим общее решение уравнения.
,
получим общее решение уравнения.
Учитывая, что
![]() ,
то
,
то![]() .
.
Ответ:
![]() .
.
В задачах №№ 211-220 все дифференциальные
уравнения - линейные первого порядка
![]() или уравнения Бернулли
или уравнения Бернулли![]() ,
,![]() и
и![]() .
.
Решение этих уравнений можно искать
в виде
![]() ,
где
,
где![]() и
и![]() ,
в результате чего уравнения записываются
в виде:
,
в результате чего уравнения записываются
в виде:
![]() -
линейное уравнение,
-
линейное уравнение,
![]() - уравнение Бернулли.
- уравнение Бернулли.
Вынесем за скобку во втором и третьем
выражении
![]() и получим
и получим
![]() - линейное уравнение,
- линейное уравнение,
![]() - уравнение Бернулли.
- уравнение Бернулли.
Тогда вместо искомого уравнения получаем два уравнения:
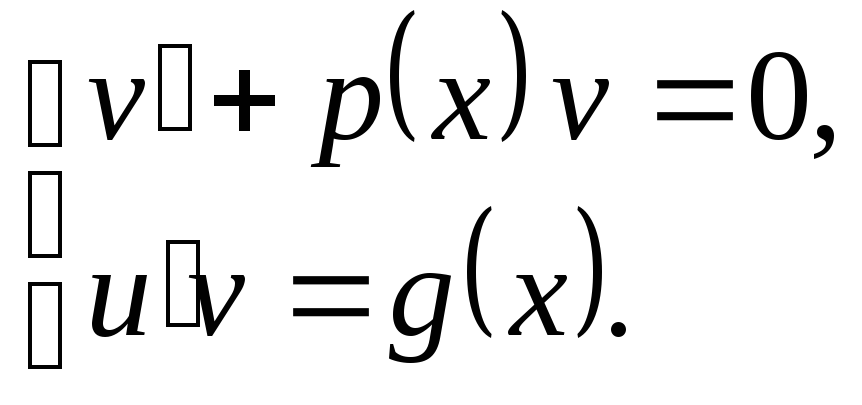 для линейного уравнения
для линейного уравнения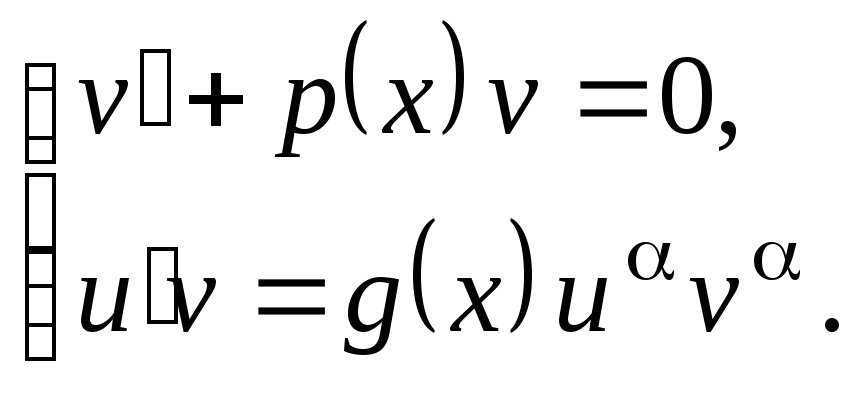 для
уравнения Бернулли.
для
уравнения Бернулли.
Последовательно решая каждое уравнение
системы, получим
![]() и
и![]() ,
а соответственно и
,
а соответственно и![]() ,
т.е. общее решение уравнения.
,
т.е. общее решение уравнения.
Пример 2. Найти частное решение дифференциального уравнения, удовлетворяющее указанному условию
![]() ,
,![]() .
.
Решение: приведем уравнение к виду
линейного или уравнения Бернулли, а для
этого разделим все выражения на
![]()
![]() .
.
Замечаем, что это уравнение Бернулли
т.к.
![]() ;
;
![]() и
и
![]() .
.
Находим решение в виде
![]() ,
тогда
,
тогда![]() .
.
Уравнение примет вид
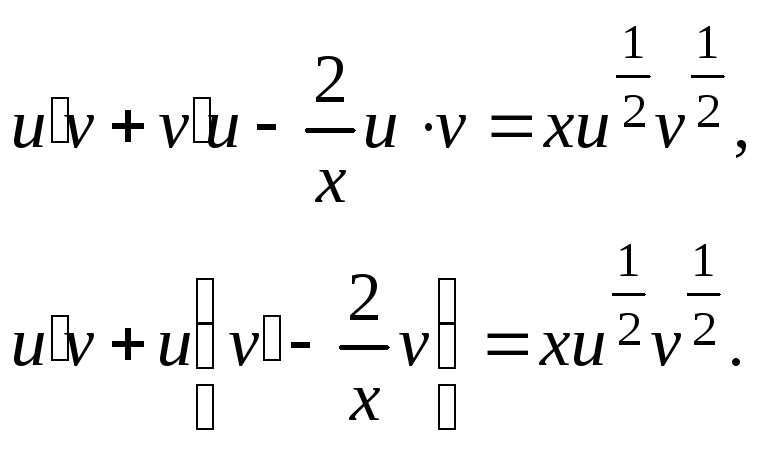
Запишем систему уравнений, для нахождения
![]() и
и![]()

![]() ,
т.к.
,
т.к.![]() ,
то
,
то![]() .
.
Разделив переменные, получим
![]() .
.
Интегрируя, получим
![]()
![]() отсюда
отсюда![]() .
.
Подставляя найденное
![]() во второе уравнение системы, получим
во второе уравнение системы, получим
![]() или
или![]() .
.
Сократив на
![]() ,
разделим переменные учитывая, что
,
разделим переменные учитывая, что![]() :
:
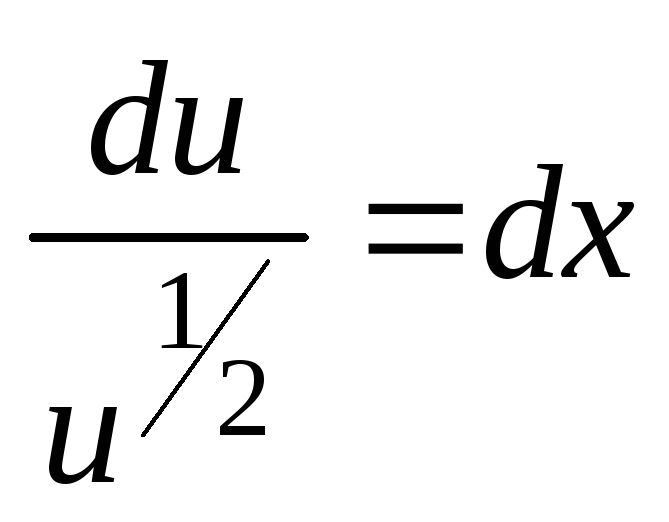 .
.
Проинтегрировав, получим
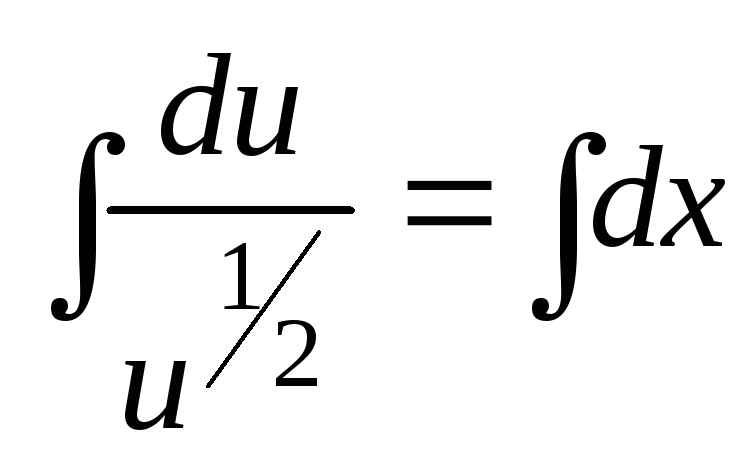 ,
,![]() ;
;![]() ;
;![]() .
.
Таким образом, общее решение имеет вид
![]()
Учитывая начальные условия
![]() выделим из семейства кривых
выделим из семейства кривых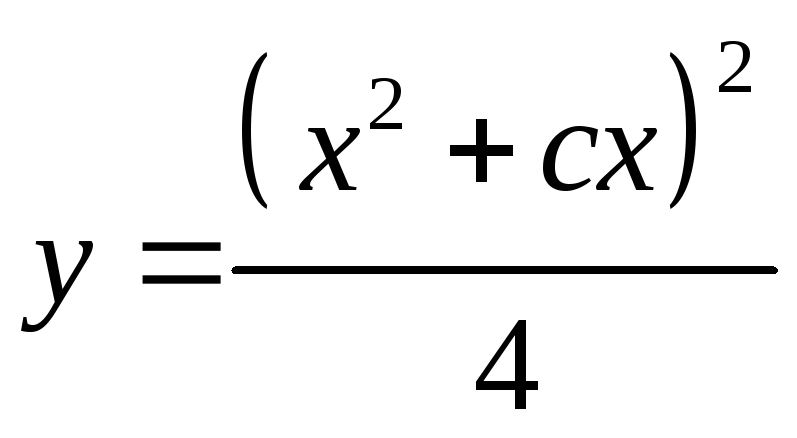 ту кривую, которая проходит через
заданную точку.
ту кривую, которая проходит через
заданную точку.![]() ,
отсюда
,
отсюда![]() и
и![]() Подставим
Подставим![]() в общее решение, получим частное решение
уравнения.
в общее решение, получим частное решение
уравнения.
Ответ:
![]() .
.
В задачах №№ 221-240 заданы дифференциальные уравнения высших порядков, допускающие понижения порядка.
Различают три вида таких уравнений, это:
 - явно выражена производная.
- явно выражена производная.
Заменяя
![]() и интегрируя, получим дифференциальное
уравнение
и интегрируя, получим дифференциальное
уравнение![]() -го
порядка
-го
порядка![]() ,
отсюда
,
отсюда![]() .
.
2)
![]() .
Это уравнение, явно не содержащее
.
Это уравнение, явно не содержащее![]() .
Замена
.
Замена![]()
![]()
![]() приводит к уравнению
приводит к уравнению![]() -го
порядка
-го
порядка
![]()
3)
![]() Уравнение не содержит явно переменную
Уравнение не содержит явно переменную![]() Замена
Замена![]()
![]() приводит к уравнению
приводит к уравнению![]() -го
порядка
-го
порядка
![]()
![]()
Даны дифференциальные уравнения второго порядка, допускающие понижения порядка. Найти частное решение, удовлетворяющее указанным начальным условиям.
Пример 3.
![]()
![]()
![]()
Решение: Выделим явно
![]() ,
получим
,
получим![]() . Уравнение вида
. Уравнение вида![]() .
.
Так как
![]() ,
то
,
то![]() или интегрируя, получим
или интегрируя, получим![]()
![]() .
.
Так как
![]() то
то
![]() .
.
Интегрируя, получим
![]() .
.
Используем интегрирование по частям
![]() ;
;![]() ;
;
![]() ;
;![]() .
.
![]() .
.
Снова используем интегрирование по
частям, вычисляя интеграл
![]() .
.
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
Итак,
![]() .
.
Учитывая начальные условия, найдем![]() и
и![]() из найденных величин
из найденных величин![]() и
и![]() .
.
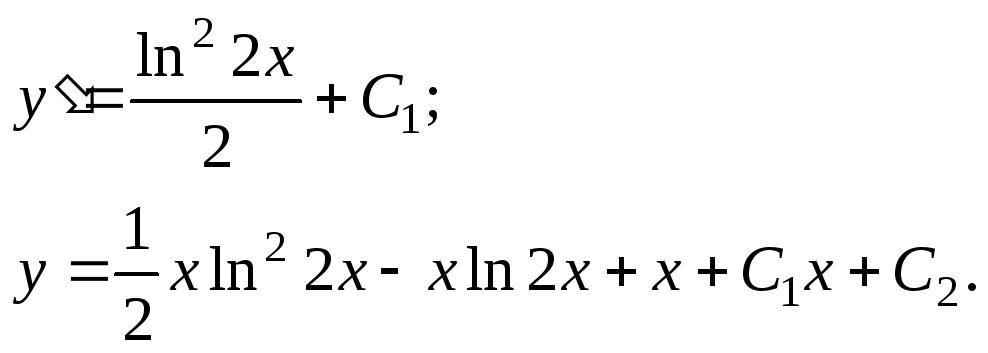
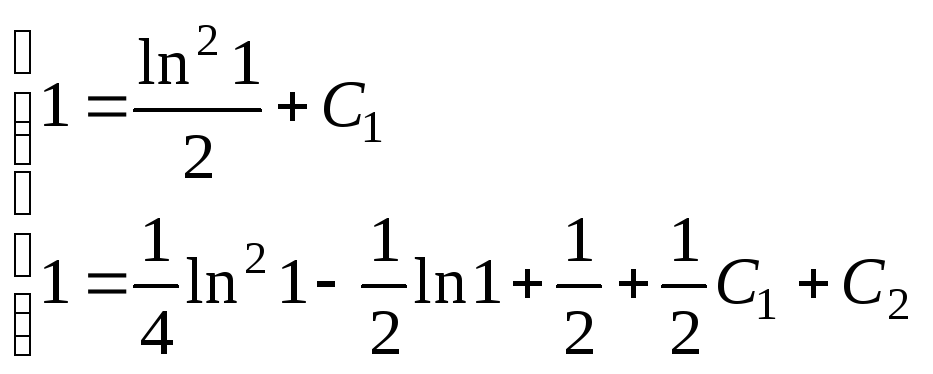 .
.
Так как
![]() ,
то
,
то
![]() .
.
Подставляя в общее решение, имеем:
![]() .
.
Ответ:
![]()
Пример 4.
![]() ,
,![]() ,
,![]() .
.
Решение: Уравнение вида
![]() .
.
Замена
![]() ,
,![]() .
.
![]() - линейное уравнение первого порядка.
Решение
- линейное уравнение первого порядка.
Решение![]() ,
,
![]() ,
,
![]() ,
,
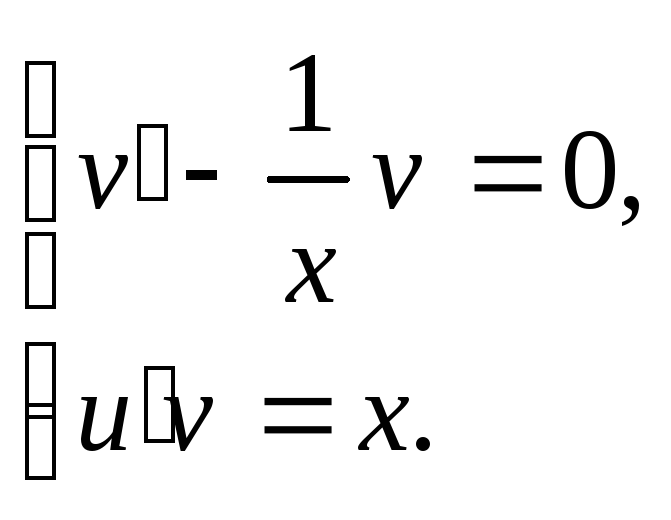
Решение первого уравнения системы:
![]() ,
,![]() ,
отсюда
,
отсюда![]() или интегрируя, получим
или интегрируя, получим
![]() ,
,![]() .
.
Подставляя во второе уравнение системы, получим
![]() ,
,![]() ,
,![]() .
.
Интегрируя, получим
![]() .
.
Так как
![]() ,
то
,
то![]() .
.
Учитывая, что
![]() ,
то
,
то![]() и
и![]() .
Интегрируя, получим
.
Интегрируя, получим
![]() .
.
Учитывая начальные условия, найдем
![]() и
и![]() из найденных величин
из найденных величин![]() и
и![]() .
.
![]() ,
,![]() .
.


Итак
![]() .
.
Ответ:
![]() .
.
Пример 5.
![]() ;
;![]() ;
;![]() .
.
Решение: уравнение вида
![]() .
.
Замена
![]() ,
,![]() .
Подставив замену в уравнение, получим
.
Подставив замену в уравнение, получим
![]() .
.
Сократим на
![]() ;
(
;
(![]() ,
отсюда
,
отсюда![]() частное решение) получим
частное решение) получим![]() .
.
Учитывая, что
![]() ,
получим
,
получим![]() .
Разделим переменные
.
Разделим переменные![]() .
Проинтегрировав выражение, получим
.
Проинтегрировав выражение, получим![]() ;
;![]() ,
или
,
или![]() .
Учитывая начальные условия
.
Учитывая начальные условия![]() ,
,![]() ,
получим
,
получим![]() .
.![]() .
.
Тогда
![]() .
Так как
.
Так как![]() ,
то
,
то![]() или
или![]() .
.
Интегрируя, получим
![]() ,
,![]() .
Учитывая, что
.
Учитывая, что![]() ,
,![]() ,
получим
,
получим![]() .
Отсюда
.
Отсюда![]() .
.
Итак,
![]() ,
отсюда найдем
,
отсюда найдем![]() .
.
![]() .
.
Ответ:
![]() .
.
В задачах №№ 241-260 все дифференциальные уравнения - линейные неоднородные с постоянными коэффициентами и специальной правой частью (ЛНДУ).
Л НДУ
– 2-го порядка имеет вид
НДУ
– 2-го порядка имеет вид![]() ;
;![]() .
.
Установлено, что, если правая часть
уравнения имеет вид, наиболее широко
встречающийся на практике,
![]() ,
то частное решение ЛНДУ находится
в виде:
,
то частное решение ЛНДУ находится
в виде:
![]() .
.
где
![]() -
число совпадений характеристики правой
части
-
число совпадений характеристики правой
части![]() с корнями характеристического уравнения,
с корнями характеристического уравнения,![]() .
.![]() и
и![]() - многочлены с неопределенными
коэффициентами, которые находим методом
неопределенных коэффициентов.
- многочлены с неопределенными
коэффициентами, которые находим методом
неопределенных коэффициентов.
Тогда решения искомого уравнения есть
![]() .
.
Пример 6. Найти частное решение, удовлетворяющее указанным начальным условиям.
![]() ,
,![]() ,
,![]() .
.
Решение: структура общего решения уравнения
![]() .
.
Составим характеристическое уравнение
![]() ,
отсюда
,
отсюда![]() и
и![]() .
.
Для данной задачи
![]() ,
,
где
![]() ,
,![]() .
.
Найдем частное решение для
![]() и
и![]() .
.
Можно представить:
![]()
Для
![]()
![]()
Тогда
![]()
Подставим это решение в уравнение, а для этого найдем первую и вторую производную
![]()
|
1 |
| |
|
-2 |
| |
|
1 |
| |
|
| ||
Сократим на 2 и приравняем коэффициенты
при
![]() и
и![]()
![]()
![]()
Итак
![]()
Для![]() имеем
имеем
Тогда
![]()
![]() .
.
Упрощая, получим
![]()
Находим производные
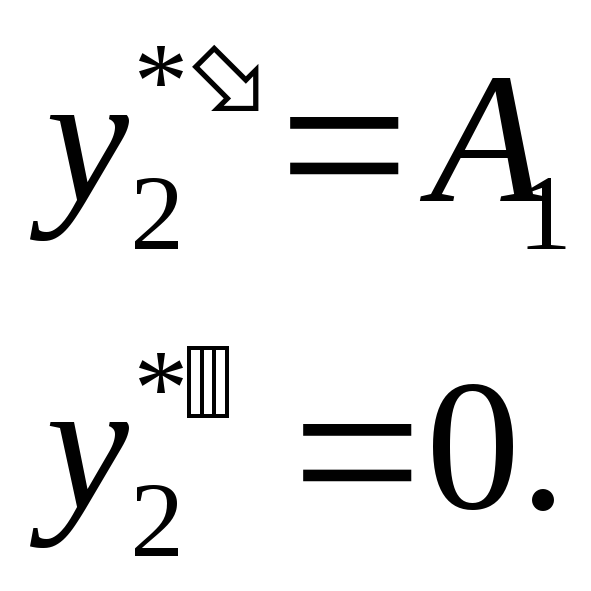
Подставим в уравнение
![]()
Приравнивая коэффициенты при одинаковых
степенях, найдем
![]() и
и![]()
![]()
![]()
Итак
![]() .
.
Общее решение уравнения
![]() .
.
Учитывая начальные условия
![]() ,
,
найдём
![]() и
и![]() Для этого найдём
Для этого найдём![]()
![]()
![]()
Итак

Или
![]()
![]()
Частное решение, удовлетворяющее указанным начальным условиям, есть
![]()
Ответ:
![]()
В задачах 261-270 заданы системы дифференциальных уравнений, решения которых можно найти методом исключения.
Пример 7. Решить систему уравнений и выделить частное решение, удовлетворяющее указанным начальным условиям.
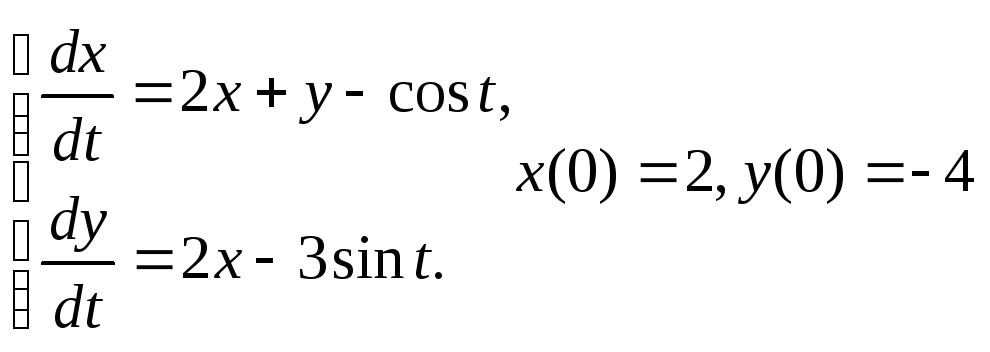 .
.
Решение.
Из первого уравнения системы найдём
![]() .
.
![]() отсюда найдём
отсюда найдём![]()
Теперь
![]() и
и![]() подставим во второе уравнение системы.
подставим во второе уравнение системы.
![]()
отсюда
![]() .
.
Получим дифференциальное уравнение второго порядка со специальной правой частью.
Структура общего решения его
![]() .
.
Составим характеристическое уравнение
![]() тогда его корни
тогда его корни
![]() .
.
![]()
Рассмотрим
![]() .
.
Итак,
![]() .
.
|
-2
-1
1 |
|
![]()
или
![]() .
.
Приравниваем коэффициенты при
![]()
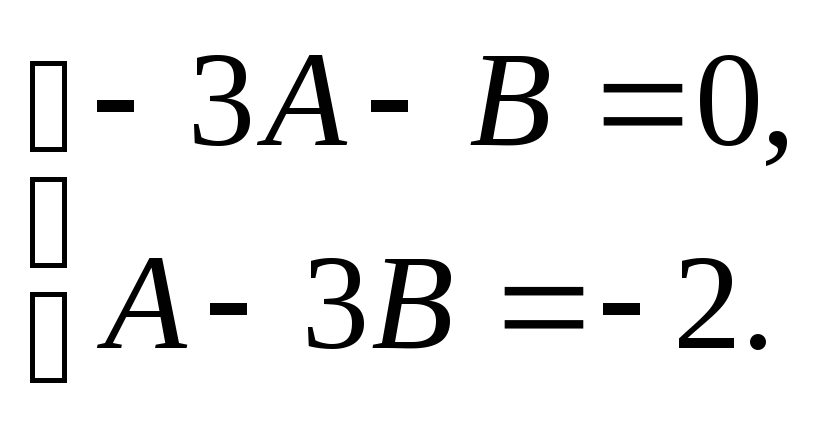
![]()
![]()
Итак ,
![]() тогда
тогда![]()
Теперь найдём
![]() Учитывая, что
Учитывая, что![]() получим
получим
![]() ,
,
![]() .
.
Итак, общее решение системы есть
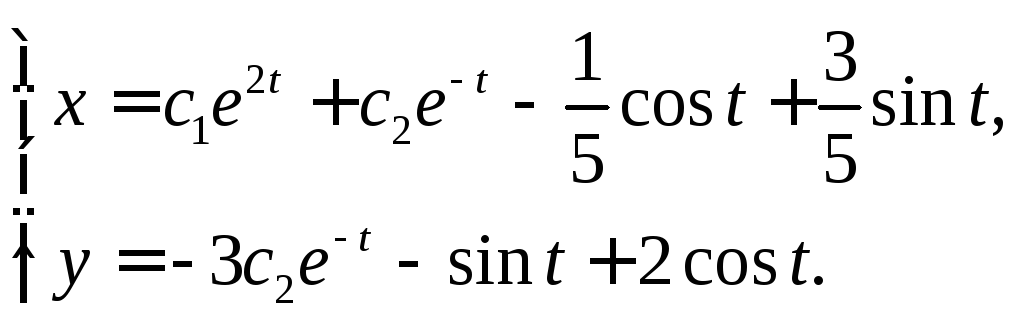
Учитывая начальные условия
![]() ,
найдем
,
найдем![]()

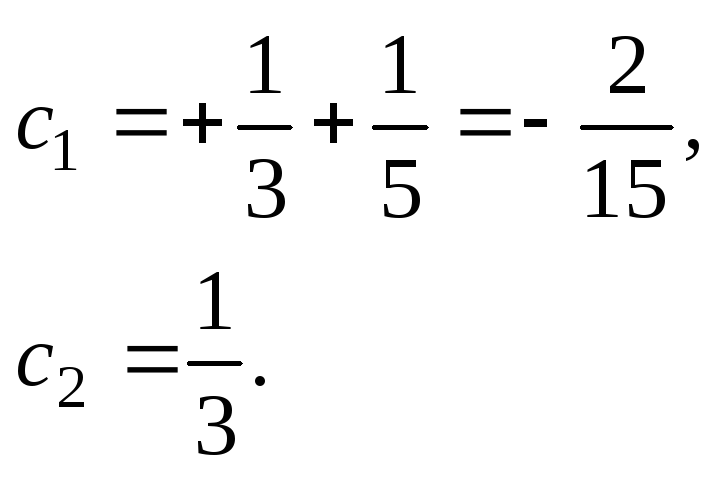
Ответ:
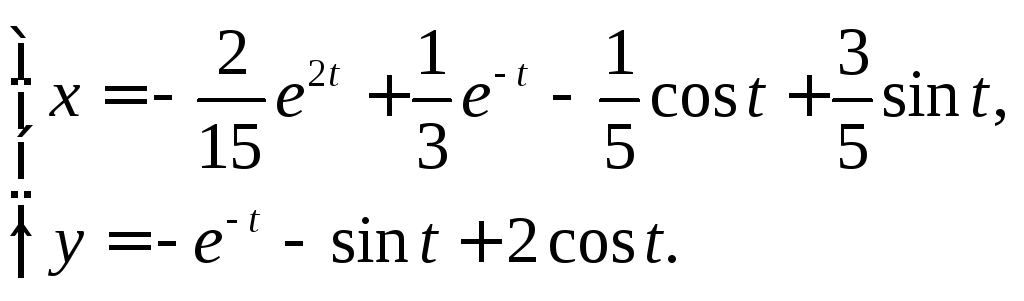
В примерах 271-280 рассмотрены задачи, при решении которых надо составить дифференциальное уравнение, и, решив его, ответить на поставленный вопрос задачи.
Пример 8. Найти кривую, проходящую через точку (3;2), для которой отрезок любой её касательной, заключенный между координатными осями, делится пополам в точке касания. Построить кривую.
Решение. Пусть,
![]() есть
середина касательной
есть
середина касательной![]() по условию являющаяся точкой касания
(точки
по условию являющаяся точкой касания
(точки![]() -
это точки пересечения касательной с
осями
-
это точки пересечения касательной с
осями![]()
![]() В
силу условия
В
силу условия![]() Угловой коэффициент касательной к
кривой в точке
Угловой коэффициент касательной к
кривой в точке![]() равен
равен![]()
![]()
![]()
Это и есть дифференциальное уравнение искомой кривой. Преобразовав, получим:
![]()
и, следовательно,
![]() или
или![]() Используя
начальное условие, определим
Используя
начальное условие, определим![]() Итак, искомая кривая есть гипербола
Итак, искомая кривая есть гипербола![]() .
.
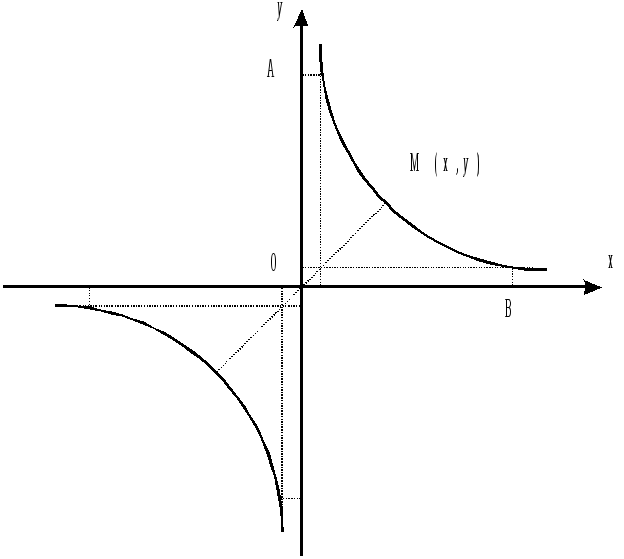
![]()
