Дин. системы / 17-18 лекция. 5.2

5.2. Тегіс динамикалық жүйелер

Динамикалық жүйелердің қозғалысын n-өлшемді евклидтік кеңістіктігінде қарастырайық.

функциясы t бойынша үзіліссіз дифференциалданатыны жиі болып шығады. t бойынша осы функцияның туындысын фазалық жылдамдық (яғни күйлердің өзгеру жылдамдығы) деп атайық және оны деп белгілейміз. Сөйтіп, - нүктесіндегі фазалық жылдамдық. Стационарлы жүйенің фазалық жылдамдығы тек осы жүйенің күйіне ғана байланысты болады. х нүктесіндегі фазалық жылдамдықды әдетте деп белгілейді, және оның күйге қатысты тәуелділігін дифференциалдық теңдеу ретінде жазады:

Стационарлы жүйелермен салыстырғанда, стационар емес жүйенің х нүктесіндегі фазалық жылдамдықғы тек қана х күйінің функциясы емес, сонымен қатар t уақытының функциясы болып табылады. (5.1) дифференциалдық теңдеудің аналогы ретінде келесі теңдеу болады:

Күйлер Е кеңістігімен қатар оған изоморфты болып келетін фазалық жылдамдықтар кеңістігін қарастырамыз. Оның Е сияқты өлшемі бар болады, бірақ оның нүктелері фазалық нүктелер болып табылады. Е және арасындағы изоморфтылық қатынасымен берілуі мүмкін, мұндағы – уақыттың өлшем бірлігі. Осындай белгілеулер кезінде (5.1) теңдеуінің f оң жағы әр нүктесіне фазалық жылдамдығына пропорционал болып келетін векторын қояды. Осы векторлардың барлық жиынтығын динамикалық жүйенің бағыттарының өрістері деп аталады.

Анықтама 1. Динамикалық жүйе тегіс деп аталады, егер оның қозғалысы оң f жағы х және t бойынша үзіліс дифференциалданатын (5.1) немесе (5.2) теңдеуімен сипатталса.

Егер - (5.1) теңдеуінің жеке шешімі болса, яғни -ді оң және сол жағына қойғанда, (5.1) қатынасы тепе-теңдікке айналатын болса, онда оны түрінде жазуға болады, мұндағы - бастапқы шарттар. Қатты дене қозғалысының динамикасын зерртеу есептерінде фазалық координаттар ретінде көбінесе кеңістік координаттарын және олардың жылдамдықтарын таңдайды.

Сызықты стационарлы динамикалық жүйелер

Е – өрісіндегі соңғы өлшемді векторлық кеңістігі болсын, ал – стационарлы динамикалық жүйесінің қозғалысы, оның фазалық кеңістігі Е болсын. Бізді θ бейнесі сызықты оператор болып табылатын жағдайы қызықтырады, яғни кез-келген скаляры үшін және кез-келген x пен y векторлары үшін қатынасы дұрыс болып табылады.

Анықтама 1. Кері динамикалық жүйесі сызықты деп аталады, егер оның Е фазалық кеңістігі векторлық кеңістік болса, ал θ қозғалысымен анықталатын бейнесі кез-келген уақыттың бекітілген моменттерінде сызықты оператор болып табылады.

Тегіс сызықты стационарлы динамикалық жүйелердің қозғалысы (5.1) түріндегі оң жағында фазалық жылдамдығы үшін теңдеуі тұратындай дифференциалдық теңдеулерімен және сипатталу қажет. f оң жағы Е-ні –де бейнелейтін оператор болып табылады. Бірақ осы жағдайда, жаза отырып, мұндағы А – сызықты оператор, күйден тәуелді фазалық жылдамдығы үшін теңдеуін аламыз. Ол біртекті сызықты дифференциалдық теңдеуімен беріледі:

(5.3) теңдеуінде х – n-өлшемді күйлердің векторы болып табылады, - сызықты оператор. (5.3) жазуына тек қана вектор-операторлы емес, сондай-ақ матрицалық мағынасын еңгізетін боламыз. Сонымен қатар, х – n-өлшемді вектор-бағана, ал А – оператордың матрицасы.

мұндағы – бастапқы шарттардың векторы, ал операторы

қатынасымен анықталады. (5.5) қатынасында t уақыты – скаляр, сондықтан операторын басқа қарапайым функцияларын сияқты уақыт бойынша дифференциалдауға болады. Сондай-ақ, осыдан (5.4) – (5.3) теңдеуінің шешімі екені шығады.

Ең қарапайым жағдайда, сипаттамалық А көпмүшелігінің [яғни ] әр түрлі n нақты түбірлері бар болса, онда Е кеңістігінде А операторының меншікті векторларынан тұратын базис бар болады. Бұл базисте А операторының матрицасы канондық жоран формасы түрінде болады, яғни

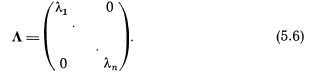
түріндегі диагонал матрицасы. Егер L деп А-ны канондық жордан формасына әкелетін ерекше емес матрицаны белгілесек, онда деп алып, және осы теңдеуді (5.3) апарып қойсақ, онда

қатынасы матрицалық теңдікті анықтайды.

Егер (5.7) теңдеуін y вектор-бағанының координаттары үшін теңдеулер жүйесі түрінде жазсақ, онда тәуелсіз бірінші ретті дифференциалдық теңдеулер жүйесін аламыз:

оның шешімін түрінде жазуға болады. Әр қозғалыс сайын сызықты операторымен байланысқан.

Осы сызықты операторының матрицасын жалып жағдайда келесі түрде жазса болады:

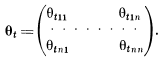
Дифференциалдық теңдеулер теориясында бағандары дифференциалдық теңдеулердің сызықты тәуелсіз шешімдері болып табылатын матрицаларды шешімдердің фундаменталды матрицалары деп аталатынын есімізге түсіріп кетейік. Сөйтіп, динамикалық жүйенің қозғалысын анықтайтын сызықты операторының матрицасы –қозғалыс дифференциалдық теңдеулерінің шешімдерінің нормаланған фундаменталды матрицасы болып табылады.

Меншікті векторлардан тұратын базисте [яғни (5.7) теңдеуі үшін] шешімдердің нормаланған фундаменталды жүйесі қарапайым диагоналды түрде болады:

Және тағы да жалпы жағдайда, сипаттамалық көпмүшенің түбірлері арасында еселіктер бар болса, онда А матрицасының канондық жордан формасының диагоналды болуы онша қажет емес. Жалпы жағдайда, канондық формасын келесі түрде жазсақ болады:

сөйтіп, матрицасы өлшемді блоктарынан тұратын болады. (5.8) теңдеуінің аналогы матрицалық дифференциалдық теңдеуі болып табылады:

(5.11) түріндегі әр теңдеуінің нормаланған фундаменталды матрицаларын арқылы белгілейміз. екені анық. деп алып,

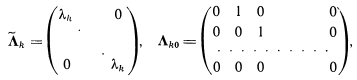
бар болады.

(5.11) түріндегі әр теңдеуінің нормаланған фундаменталды матрицасы келесі түрінде жазылатындығы тікелей тексеріледі: