
09-01-2015_09-46-11 / Лекция 10. ТВ и МС
.pdf
Лекция 10 Числовые характеристики случайных величин. Математическое ожидание и
ее свойства. Определение дисперсии. Свойства дисперсии. Ковариация , коэффициент корреляции и их свойства.
Математическое ожидание дискретной случайной величины
Пусть случайная величина ξ– есть некоторый денежный выигрыш в азартной игре. Хотелось бы заранее , оценить, на какой средний выигрыш можно
рассчитывать , начиная игру. |
|
|
Пусть , например, игра состоит в бросании игральной кости : |
выигрыш в |
|
(тг ) при каждом бросании равен числу, выпавшему на |
грани . Пусть игральную |
|
кость бросили n раз. При этом единица выпала m1 |
раз, двойка m2 |
раз, и т.д. |
( m1 + m2 + …+m6 =n ) Общий выигрыш составит |
|
|
S = 1m1 +2m2 +3m3 +4m4 +5m5 +6m6
Значит, на одно бросание приходится средний выигрыш, равный
s =S/n= 1/n(1m1 +2m2 +3m3 +4m4 +5m5 +6m6 )= 1m1/n +2m2 /n+3m3 /n +4m4/n +5m5/
n+6m6/n
Ксожалению, эту величину можно посчитать только после опытов.
Заметим, что величины mi/n (i=1,2,..,6) есть относительные частоты выпадения числа i . Из закона статистической устойчивости ( фундаментального
свойства случайного события) |
нам известно, что при большом числе испытаний |
||||||||||||
относительная частота |
стабилизируется около |
значения вероятности. Поэтому , |
|||||||||||
чтобы |
оценить |
средний выигрыш до игры |
, можно заменить в формуле |
||||||||||
относительные частоты на соответствующие вероятности – ведь вероятности |
|||||||||||||
можно просчитать до игры, не проводя экспериментов. |
|||||||||||||
Таким образом , s ≈ m = 1p1 +2p2 +3p3 +4p4 +5p5 +6p6 |
|||||||||||||
p1 =p2 =p3 = p4 = p5 = p6 =1/6 , |
|
|
|
m = (1+2+3+4+5+6)/6=3,5 |
|||||||||
С бросанием игральной кости |
связана случайная величина ξ |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ |
|
x |
x |
|
x |
x |
x |
x |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
1/6 |
1/6 |
|
1/6 |
1/6 |
|
|
1/6 |
1/6 |
|
|
|
Математическим ожиданием конечной случайной величины ξ |
||||||||||||
|
|
|
|
|
|
|
ξ = |
|
|
i=1,2,…,n |
|||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
называется число Mξ = x1 p1 + x2 p2 +…+xn pn =  xi pi
xi pi
Математическое ожидание случайной величины характеризует ее среднее , «ожидаемое» значение (прогноз)
29

Если дискретная случайная величина ξ принимает счетное множество значений x1 , x2 , …,xn ,… , то математическое ожидание такой дискретной
случайной величины называется сумма ряда : Mξ =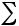 xi pi
xi pi
Так как ряд может расходиться , то соответствующая случайная величина может и не иметь математическое ожидания Пример Бросание монеты до первого появления герба. Пусть случайная величина ξ характеризует число бросаний монеты.
ξ |
2 |
22 |
… |
2i |
… |
p |
1/2 |
1/22 |
… |
1/2i |
… |
Эта случайная величина не имеет математического ожидания
2i /2i = 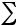 1=∞
1=∞
На практике, как правило, множество возможных значений случайной величины распространяется лишь на ограниченный участок оси абсцисс и, значит, математическое ожидание существует.
Свойства математического ожидания
1. Математическое ожидание постоянной равно ей самой : Мс=с
Доказательство. По определению с= 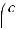
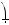 Mc=c 1=c
Mc=c 1=c
2.Если случайная величина ξ принимает только неотрицательные значения ξ ≥
0, то Mξ ≥ 0
3.M(cξ) = cMξ
Доказательство. |
|
M(cξ) = cx1 p1 +cx2 p2 +…+cxm pm =c |
= cMξ |
|||
4. M( ξ |
η) = Mξ |
Mη |
|
|
||
Доказательство. |
|
M( ξ + η)= |
(xi + yj )pij = |
|
||
| где pij =P{ ξ =xi ,η =yj } совместные вероятности ξ и η | = |
||||||
= xi |
pij + |
yj pij |
= xi(pi1 |
+pi2 +…) + yj(p1j +p2j |
+…)= = xipi + |
|
yjqj = Mξ |
+ |
Mη |
|
|
|
|
5. Для любой случайной величины справедливо равенство M(ξ - Mξ) =0
Доказательство . M(ξ - Mξ) = Mξ - M(Mξ) = Mξ - Mξ =0 использовали свойства 4) и 1)
Случайная величина |
= ξ - Mξ называется центрированной |
30

6. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:
M( ξ η) = Mξ Mη
Доказательство. По определению M( ξη) = 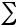 xi yj pij = | однако ξ и η
xi yj pij = | однако ξ и η
независимы pij |
=pi qj | |
|
= |
xi yj pi qj = ( |
xipi )( yjqj ) = Mξ Mη |
Итак, математическое ожидание характеризует среднее значение случайной величины. Говорят, что математическое ожидание – характеристика положения или центральных тенденций.
|
|
|
5.3.2. Дисперсия |
|
|
|||
|
Дисперсией случайной величины ξ |
называется число Dξ = M(ξ - Mξ)2 |
||||||
Дискретная случайная величина (ξ - Mξ)2 |
распределена по закону |
|||||||
|
|
|
|
|
|
|
|
|
|
(ξ - Mξ)2 |
(x1 - Mξ)2 |
(x2 - Mξ)2 |
… |
|
(xi - Mξ)2 |
…. |
|
|
P |
P1 |
P2 |
…. |
|
Pi |
….. |
|
и по определению математического ожидания , дисперсия дискретной случайной величины вычисляется по формуле :
Dξ=  (xi - Mξ)2 pi
(xi - Mξ)2 pi
Число σ =  называется среднеквадратичным отклонением или стандартным отклонением случайной величины ξ .
называется среднеквадратичным отклонением или стандартным отклонением случайной величины ξ .
Свойства дисперсии
1.D ξ ≥ 0; D ξ = 0 ξ = const
2.D ( cξ) = c2 D ξ
Доказательство .D (cξ )=M (cξ - M(cξ ) )2 = M(cξ - c Mξ)2 =M(c2 (ξ - Mξ)2 ) = c M (ξ - Mξ)2 = c2 D ξ
! В частности D ( -ξ) = D ξ
3. Сдвиг на константу не меняет дисперсии D (ξ + c ) = D ξ
Доказательство. D (ξ + c ) =M [ ξ + c – M(ξ + c) ]2 = M [ ξ + c – Mξ - c ]2 = M [ ξ
–Mξ ) ]2 = D ξ
Вчастности в качестве константы можно взять (- М ξ ) . Тогда получаем , что
дисперсия центрированной случайной величины = ξ - Mξ |
равна дисперсии |
ξ , т.е. D = D ξ |
|
Из свойств 2) и 3) D(aξ + b)=a2 Dξ |
|
31
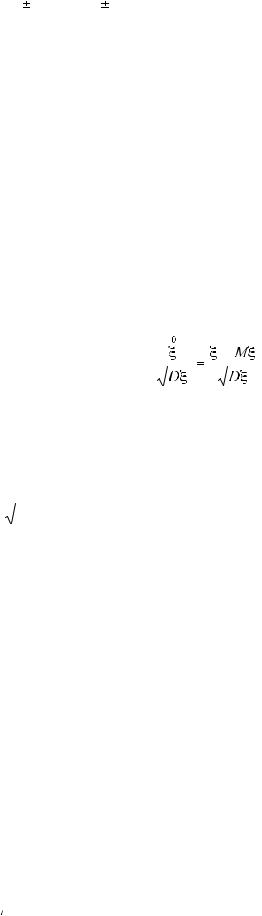
4. D ( ξ η) = Dξ |
Dη |
( ξ и η независимы ) |
Доказательство. |
D(ξ + η ) = M[(ξ + η ) – M(ξ + η ) ]2 = |
|
M[(ξ – Mξ ) + (η - Mη ) ]2 =
=M[(ξ – Mξ )2 +2(ξ – Mξ ) (η - Mη ) + (η - Mη )2 ]= M(ξ – Mξ )2 + M (η - Mη )2 +2M[(ξ – Mξ ) (η - Mη )]
По условию случайные величины ξ и η независимы , следовательно независимы и центрированные случайные величины ξ – Mξ , η - Mη . Значит
M[(ξ – Mξ ) (η - Mη )] =M(ξ – Mξ )M (η - Mη ) =0 5. D ξ =Mξ2 - (Mξ)2
Доказательство.
D ξ = M(ξ - Mξ)2 =M[ ξ2 -2 ξ Mξ+(Mξ )2 ] = Mξ2 - 2M(ξMξ) + M(Mξ)2 = Mξ2 - 2Mξ Mξ + (Mξ)2=Mξ2 - (Mξ)2
Случайная величина ξ*= |
|
|
|
|
|
|
|
|
|
называется стандартизированной |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
( нормированной) .
Стандартизированная случайная величина имеет нулевое математическое ожидание и единичную дисперсию
Mξ* =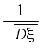 M(ξ - Mξ) =0
M(ξ - Mξ) =0
Dξ* =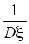 D(ξ - Mξ)=
D(ξ - Mξ)=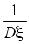 Dξ =1
Dξ =1
Пример В урне 3 черных и 2 белых шара . Из урны наугад вынимают 2 шара. Случайная величина ξ – число белых шаров среди вынутых. Найти закон распределения ξ , математическое ожидание и дисперсию.
Решение.
ξ |
0 |
1 |
2 |
р |
0,3 |
0,6 |
0,1 |
|
|
|
|
P(ξ=0)=(3/5)(2/4)=0,3 P(ξ=1)=(2/5)(3/4)+ (3/5)(2/4)==0,6 P(ξ=2)=(2/5)(1/4)=0,1
Mξ=0 0,3+1 0,6+2 0,1=0,8
Dξ= 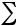 (xi - Mξ)2 pi =(0-0,8)2 0,3+(1-0,8)2 0,6+(2-0,8)2 0,1=0,36
(xi - Mξ)2 pi =(0-0,8)2 0,3+(1-0,8)2 0,6+(2-0,8)2 0,1=0,36
Теперь вычислим дисперсию по формуле свойства 5) Mξ2=0 0,3+1 0,6+4 0,1=1
D ξ =Mξ2 - (Mξ)2 =1- 0,82 =0,36
32

Моменты высших порядков
Математическое ожидание и дисперсия являются частными случаями более общего понятия как моменты случайных величин .
Начальным моментом k-го порядка случайной величины ξ называется
αk = Mξk
Следовательно, математическое ожидание α1 = Mξ - это начальный момент первого порядка.
Центральным моментом k -го порядка случайной величины ξ называется
k =M(ξ- Mξ)k
1 = M(ξ - Mξ) =02 = M(ξ - Mξ)2 = Dξ
Т.е. дисперсия - это центральный момент второго порядка.
Центральные моменты можно выразить через начальные моменты , например для k =2 :
D ξ =Mξ2 - (Mξ)2 =α2 - (α1 )2
5.3.3. Ковариация и корреляция случайных величин
Ковариацией случайных величин ξ и η называется число
(5.2) cov (ξ , η ) = M(ξ - Mξ )( η -Mη)
Свойства ковариации
1)cov (ξ , η) = cov (η, ξ )
2)cov (ξ , ξ ) =Dξ
Доказательство cov (ξ , ξ ) =M( ξ - Mξ )2 =Dξ 3) cov (ξ+ c1 , η + c2 ) = cov (ξ , η)
Доказательство
cov (ξ+ c1 , η+ c2 ) =M(ξ+ c1 –M(ξ+ c1))( η+ c2 – M(η + c2 ))=
| M(aξ + b )= aMξ + b | = M(ξ+ c1 –Mξ -c1)( η+ c2 – Mη- c2 ) = = M(ξ –Mξ )( η– Mη) = cov (ξ , η)
4) cov (c1 ξ + c2 η, ζ )=c1 cov (ξ , ζ)+ c2 cov (η , ζ) , c1 , c2 = const
Доказательство
cov (c1 ξ + c2 η, ζ )=M(c1 ξ + c2η- M(c1 ξ + c2 η))( ζ-Mζ) =
= M(c1 ξ + c2η- c1 Mξ - c2 Mη )( ζ-Mζ) = M(c1 (ξ - Mξ ) +c2 (η - Mη))( ζ-Mζ)= =M(c1 (ξ - Mξ ) (ζ -Mζ)+c2 (η - Mη) (ζ-Mζ)) =
=c1 M(ξ - Mξ ) (ζ-Mζ)+c2 M(η - Mη ) (ζ-Mζ) =c1 cov (ξ , ζ)+ c2 cov (η , ζ)
5) D(ξ η) = Dξ + Dη 2 cov (ξ ,η ) |
ξ , η |
(5.3) |
|
Доказательство. |
D(ξ + η)=Dζ=M(ζ - Mζ)2= M(ξ + η -M(ξ + η))2= |
||
= M(ξ + η -Mξ - Mη)2 =M(ξ- Mξ + η - Mη)2 =
=M(ξ- Mξ)2 +2M(ξ- Mξ)( η - Mη)+M(η - Mη)2 = Dξ + Dη + 2 cov (ξ ,η ) 6) (5.4) cov (ξ , η) = Mξ η- Mξ Mη
33
Доказательство. |
cov (ξ , η ) = M(ξ - Mξ )( η -Mη) = |
|
=M(ξη -ξ Mη-η Mξ + Mξ Mη)= Mξ η - MηMξ - MξMη+ Mξ Mη= Mξη- Mξ Mη |
||
7) Если ξ и η независимы, то cov (ξ , η) = 0 |
|
|
Доказательство. |
Так как Mξi ξj = Mξi Mξj , если ξ и η независимы, то из (5.4) |
|
следует, что cov (ξ , η) = 0 |
|
|
Для независимых случайных величин cov (ξ , η) = 0 |
, следовательно, если |
|
cov (ξ , η) ≠ 0 , то случайные величины ξ и η зависимы |
||
Ковариационной матрицей случайного вектора |
ξ = (ξ1 , ξ2 , …,ξn ) |
|
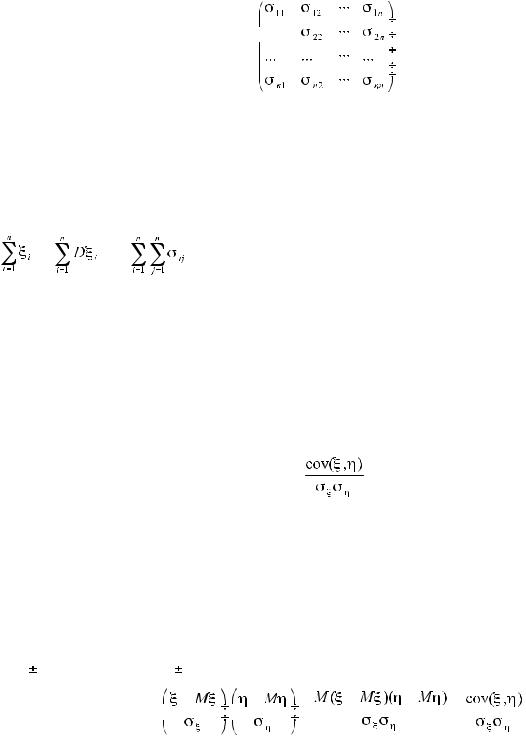
называется матрица Σ , элементами которой являются ковариации
σij = cov (ξi , ξj ) :
Σ = 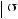
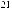
Из свойств ковариации вытекает, что ковариационная матрица является симметричной σij= σji и ее диагональные элементы равны дисперсиям случайных
величин |
ξ1 , ξ2 , …,ξn : σii =Dξi |
|
|
Используя введенные обозначения, заметим, что формула (5.3) может быть |
|
обобщена на любое число слагаемых |
||
D( |
)= |
+ 2 |
Ковариация характеризует не только степень зависимости двух случайных величин, но и их разброс, рассеяние. Кроме того, она – величина размерная, ее размерность определяется произведением размерностей случайных величин. Это
затрудняет использование ковариации для оценки степени |
зависимости для |
различных случайных величин. Этих недостатков лишен |
коэффициент |
корреляции. |
|
Коэффициентом корреляции двух случайных величин называется отношение их ковариации к произведению средних квадратичных отклонений этих величин:
ρξη =
Коэффициент корреляции есть безразмерная величина
Свойства коэффициента корреляции
1) |
ρξη |
= ρηξ |
|
|
|
|
|
|
|
|
|
|
|||||||||
2) |
Коэффициент корреляции принимает значения на отрезке [-1;1] : |
||||||||||||||||||||
|
|
-1 |
|
≤ ρ ≤ 1 |
|
|
|
|
|
||||||||||||
Доказательство. Обозначим через |
X= (ξ - Mξ) /σξ |
|
, Y =( η - Mη) /ση |
||||||||||||||||||
MX=MY=0; DX = DY = 1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
D(X |
Y) = DX + DY 2 cov (X ,Y ) |
|
|
|
|
|
|||||||||||||||
cov( X, Y )=M(X,Y)=M |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
= |
|
=ρξη |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
34

Следовательно, D( X Y ) = 2 2ρξη ≥0 , т.е. |
1 ρξη ≥0 |
1+ ρξη ≥0 , ρξη ≥ -1 , |
|
1 - ρξη ≥0 , ρξη ≤ 1 |
|
-1 ≤ ρ ≤ 1 |
|
3) Если случайные величины ξ и η независимы, то ρξη =0. Доказательство. Так как ξ и η независимы , то cov (ξ ,η ) =0
Случайные величины называются некоррелированными, если их коэффициент корреляции равен нулю.
Если случайные величины независимы, то они некоррелированы. Обратное утверждение, вообще говоря, неверно: из некоррелированности двух случайных величин еще не следует их независимость
4) | ρξη |
| = 1 ξ и η связаны линейной зависимостью, т.е. |
||||||||
η = aξ + b |
, |
где |
а и b - постоянные, причем ρξη =1 , если a > 0 и |
||||||
ρξη = -1 , если a < 0. |
|
|
|
|
|
|
|||
Доказательство. Обозначим через |
X= (ξ - Mξ) /σξ |
, Y =( η - Mη) /ση |
|||||||
Тогда D(X |
Y)=M(X |
|
Y)2 – (M(X |
Y))2 = |
|
||||
| т.к. случайные величины Х и У центрированные , то (M(X Y))2 =0 | |
|||||||||
= M(X |
Y)2 = DX + DY |
2 cov (X ,Y ) |
|
|
|||||
Поэтому |
M(X |
Y)2 =2 |
2ρξη |
≥0 |
|
|
|
||
ρξη = |
1 , 2 2ρξη = 0 |
|
|
|
|
|
|
||
|
|
Т.е., если |
ρξη=1 , то |
1- ρξη =0 |
|
||||
|
|
|
если |
ρξη=-1 , то |
1+ ρξη =0 |
|
|||
Следовательно, |
M(X |
|
Y)2 =0 |
при |
ρξη = |
1 |
|||
Равенство математического ожидания неотрицательной случайной величины нулю означает , что сама случайная величина тождественно равна нулю
(X |
Y)2 =0 |
(X |
Y) =0 |
Вернувшись к исходным переменным , получаем
(ξ - Mξ) /σξ |
( η - Mη) /ση = 0 , |
ρξη = 1 , |
|||||
Следовательно, |
|
|
|
|
|
||
η = Mη |
|
(ξ - Mξ) |
|
|
|
||
|
|
|
|
||||
Если обозначим |
b = Mη |
|
Mξ , a = ± |
|
|
||
|
|
||||||
То получим , что |
η = aξ + b. |
|
|
|
|||
Коэффициент корреляции можно рассматривать как характеристику линейной взаимозависимости случайных величин ξ и η
35
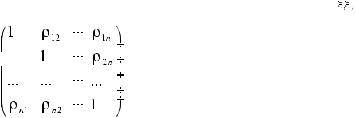
Корреляционной матрицей случайного вектора ξ = (ξ1 , ξ2 , …,ξn ) называется матрица R , элементами которой являются коэффициенты корреляции ρij = 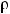
R=
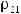
Диагональные элементы R равны единице, т.к.
ρij =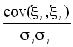 =1
=1
36
