Новая папка / s_r_6_vishka

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

Чорноморський державний університет імені Петра Могили

Факультет комп’ютерних наук

Кафедра прикладної та вищої математики

Самостійна робота № 6

Тема: «Звичайнi диференцiальнi рiвняння вищих порядкiв»

Варіант №11

Виконав:

студентка 101 групи

Спеціальності «Комп’ютерні науки»

Костік Світлана Сергіївна

Перевірив:

доктор технічних наук,

професор кафедри прикладної

та вищої математики

Дихта Леонід Михайлович

Миколаїв 2014

Завдання 10.11

Умова:

Знайти загальний розв’язок диференціального рівняння

Розв’язання:

Розділимо обидві частини на :

Це рівняння Ейлера. Його розв’язком буде сума загального та частинного розв’язку:

Тоді загальний розв’язок буде виглядати так:

Знайдемо частинний розв’язок неоднорідного рівняння:

Тоді сумарний розв’язок:

Відповідь:

Завдання 11.11

Умова:

Знайти розв’язок задачі Коші:

Розв’язання:

Продиференціюємо наступну заміну змінної:

Запишемо рівняння з новими змінними:

Оскільки , то

Проінтегруємо ліву і праву частини рівняння:

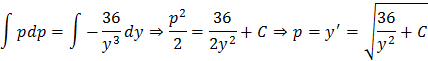
Використовуємо , :

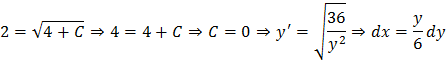
Визначаємо значення константи А:

Таким чином:

Відповідь:

Завдання 12.11

Умова:

Знайти загальний розв’язок диференціального рівняння:

Розв’язання:

- це неоднорідне лінійне диференціальне рівняння 3-го порядку. Його розв’язком є сума загального розв’язку однорідного рівняння і частинного розв’язку неоднорідного. Знайдемо загальний розв’язок, склавши характерне рівняння:

Тоді загальний розв’язок:

Тепер знаходимо частинний розв’язок неоднорідного рівняння:

Тоді повний розв’язок диференціального рівняння:

Відповідь:

Завдання 13.11

Умова:

Знайти загальний розв’язок диференціального рівняння:

Розв’язання:

- це неоднорідне лінійне диференціальне рівняння 3-го порядку. Його розв’язком є сума загального розв’язку однорідного рівняння і частинного розв’язку неоднорідного. Знайдемо загальний розв’язок, склавши характерне рівняння:

Тоді загальний розв’язок:

Тепер знаходимо частинний розв’язок неоднорідного рівняння:

Запишемо три похідні цього розв’язку:

Знайдемо коефіцієнти:

Складемо систему з двох рівнянь:

Підставимо ці значення в формулу для частинного розв’язку неоднорідного рівняння і знайдемо його:

Тоді повний розв’язок диференціального рівняння:

Відповідь:

Завдання 14.11

Умова:

Знайти загальний розв’язок диференціального рівняння:

Розв’язання:

- це неоднорідне лінійне диференціальне рівняння 2-го порядку. Його розв’язком є сума загального розв’язку однорідного рівняння і частинного розв’язку неоднорідного. Знайдемо загальний розв’язок, склавши характерне рівняння:

Тоді загальний розв’язок:

Тепер знаходимо частинний розв’язок неоднорідного рівняння:

Тоді загальний розв’язок:

Відповідь:

Завдання 15.11

Умова:

Знайти загальний розв’язок диференціального рівняння:

Розв’язання:

- це неоднорідне лінійне диференціальне рівняння 2-го порядку. Його розв’язком є сума загального розв’язку однорідного рівняння і частинного розв’язку неоднорідного. Знайдемо загальний розв’язок, склавши характерне рівняння:

Тоді загальний розв’язок:

Тепер знаходимо частинний розв’язок неоднорідного рівняння:

Тоді загальний розв’язок:

Відповідь:

Завдання 16.11

Умова:

Знайти розв’язок задачі Коші:

Розв’язання:

- це неоднорідне лінійне диференціальне рівняння 2-го порядку.

Знайдемо загальний розв’язок, склавши характерне рівняння:

Тоді загальний розв’язок:

Тепер знаходимо частинний розв’язок неоднорідного рівняння, використовуючи метод варіацій довільних постійних. Для цього перейдемо від довільних констант

і до функцій і :

(*)

Накладемо додаткову умову:

Разом з рівнянням, яке ми отримуємо після підстановки функції (*) в вихідне диференціальне рівняння, ми отримуємо систему рівнянь з двома змінними:

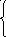
Виразимо через за допомогою першого рівняння цієї системи:

Використавши друге рівняння системи, отримаємо наступні вирази:

(де B - константа)

Тепер знайдемо :

(де A - константа)

Знайдемо першу похідну від отриманого виразу:

Знайдемо А і В:

Тоді розв’язок задачі Коші виглядатиме так:

Відповідь: