- •Понятие предела последовательности
- •Вычисление пределов вида
- •Вычисление пределов вида
- •Вычисление пределов вида
- •Понятие предела функции
- •Понятие непрерывности функции в точке
- •Вычисление пределов вида
- •Вычисление пределов вида
- •Вычисление пределов вида
- •Вычисление пределов вида
- •Вычисление пределов вида
- •Вычисление пределов вида
Понятие предела последовательности
Постановка задачи.Пользуясь определением предела последовательности, доказать, что
![]()
План решения.
1.
По определению число
![]() называется
пределом числовой последовательности
называется
пределом числовой последовательности![]() ,
если
,
если![]() .
Это
означает, что
.
Это
означает, что![]() неравенство
неравенство![]() имеет
решение
имеет
решение![]() .
.
2.
Находим, при каких
![]() справедливо
неравенство
справедливо
неравенство
![]() ,
,
т.е.
решаем это неравенство относительно
![]() .
.
3.
Если решение имеет вид
![]() ,
то
,
то![]() –
предел числовой последовательности
–
предел числовой последовательности![]() .
.
Замечание.
Если решение неравенства![]() нельзя
представить в виде
нельзя
представить в виде![]() ,
то число
,
то число![]() не
является пределом последовательности.
не
является пределом последовательности.
Задача
1.Доказать, что![]() (указать
(указать![]() ).
).
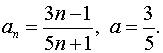
Покажем,
что для любого ![]() существует такой номер
существует такой номер![]() ,
что
,
что![]() для
всех
для
всех![]() .
.
 .
.
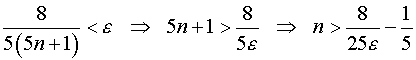 .
.
Из
последнего неравенства следует, что
можно выбрать
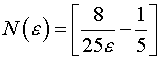 (квадратные
скобки означают целую часть) и при любых
(квадратные
скобки означают целую часть) и при любых![]() будет
выполняться неравенство
будет
выполняться неравенство![]() .
Значит, по определению предела
последовательности
.
Значит, по определению предела
последовательности
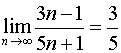 .
.
Вычисление пределов вида
Постановка задачи.Вычислить предел
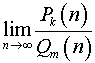 ,
,
где
![]() ,
,
![]() .
.
План решения.
Здесь
![]() –
многочлен степени
–
многочлен степени![]() (бесконечно
большая последовательность порядка
(бесконечно
большая последовательность порядка![]() )
и
)
и![]() – многочлен степени
– многочлен степени![]() (бесконечно
большая последовательность порядка
(бесконечно
большая последовательность порядка![]() ).
).
1.
Вынесем в числителе множитель
![]() ,
получим
,
получим![]() ,
где
,
где![]() .
.
2.
Вынесем в знаменателе множитель
![]() ,
получим
,
получим![]() ,
где
,
где![]() .
.
3. Имеем
 .
.
4. Получаем, что
если
![]() ,
то
,
то ;
;
если
![]() ,
то
,
то ;
;
если
![]() ,
то по теореме о пределе частного
,
то по теореме о пределе частного
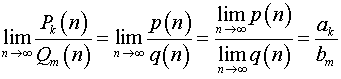 .
.
Задача 2. Вычислить пределы числовых последовательностей.

Вычисление пределов вида
Постановка задачи. Вычислить предел
 ,
,
где
![]() –
бесконечно большая последовательность
порядка
–
бесконечно большая последовательность
порядка![]() и
и![]() –
бесконечно большая последовательность
порядка
–
бесконечно большая последовательность
порядка![]() (
(![]() ).
).
План решения.
1.
Вынесем в числителе множитель
![]() ,
получим
,
получим![]() ,
где
,
где![]() .
.
2.
Вынесем в числителе множитель
![]() ,
получим
,
получим![]() ,
где
,
где![]() .
.
3. Имеем
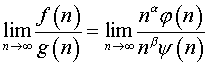 .
.
4. Получаем, что
если
![]() ,
то
,
то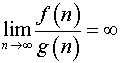 ;
;
если
![]() ,
то
,
то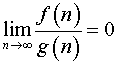 ;
;
если
![]() ,
то по теореме о пределе частного
,
то по теореме о пределе частного
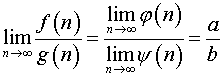 .
.
Задача 3. Вычислить пределы числовых последовательностей.

Вычисление
пределов вида
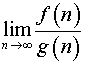
Постановка задачи.Вычислить предел
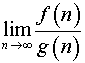 ,
,
где
![]() –
бесконечно большая последовательность
порядка
–
бесконечно большая последовательность
порядка![]() и
и![]() –
бесконечно большая последовательность
порядка
–
бесконечно большая последовательность
порядка![]() (
(![]() ).
).
План решения.
1.
Вынесем в числителе множитель
![]() ,
получим
,
получим![]() ,
где
,
где![]() .
.
2.
Вынесем в числителе множитель
![]() ,
получим
,
получим![]() ,
где
,
где![]() .
.
3. Имеем
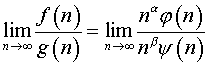 .
.
4. Получаем, что
если
![]() ,
то
,
то ;
;
если
![]() ,
то
,
то ;
;
если
![]() ,
то по теореме о пределе частного
,
то по теореме о пределе частного
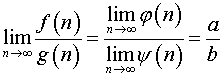 .
.
Замечание.Иногда необходимо привести выражение, стоящее после знака предела, к соответствующему виду.
Задача 4. Вычислить пределы числовых последовательностей.
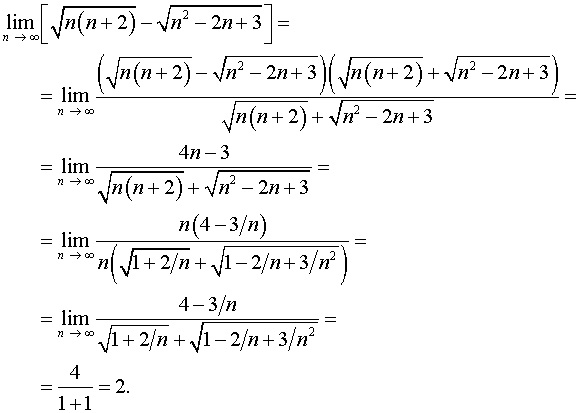
Вычисление
пределов вида
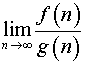
Постановка задачи. Вычислить предел
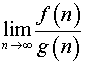 ,
,
где
![]() –
бесконечно большая последовательность
порядка
–
бесконечно большая последовательность
порядка![]() и
и![]() –
бесконечно большая последовательность
порядка
–
бесконечно большая последовательность
порядка![]() (
(![]() ).
).
План решения.
1.
Вынесем в числителе множитель
![]() ,
получим
,
получим![]() ,
где
,
где![]() .
.
2.
Вынесем в числителе множитель
![]() ,
получим
,
получим![]() ,
где
,
где![]() .
.
3. Имеем
 .
.
4. Получаем, что
если
![]() ,
то
,
то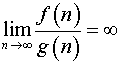 ;
;
если
![]() ,
то
,
то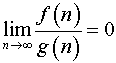 ;
;
если
![]() ,
то по теореме о пределе частного
,
то по теореме о пределе частного
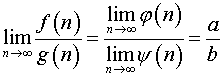 .
.
Замечание. Иногда необходимо привести выражение, стоящее после знака предела, к соответствующему виду.
Задача 5. Вычислить пределы числовых последовательностей.
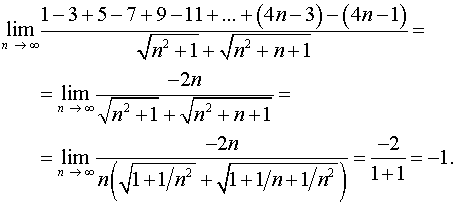
Вычисление пределов вида
Постановка задачи.Вычислить предел последовательности
![]() ,
,
где
![]() и
и![]() .
.
План решения.
1. Преобразуем выражение под знаком предела так, чтобы использовать второй замечательный предел, т.е. выделим единицу:
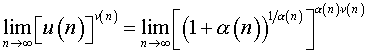 ,
,
где
![]() –
бесконечно малая последовательность
при
–
бесконечно малая последовательность
при![]() .
Так как
.
Так как![]() при
при![]() ,
то
,
то
![]() .
.
2.
Если
![]() (
(![]() )
и
)
и![]() ,
то
,
то
![]() .
.
Следовательно, если существует предел
![]() ,
,
то окончательно имеем
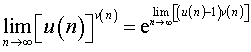 .
.
Задача 6. Вычислить пределы числовых последовательностей.