
Краткая теория
В механике под ударом следует понимать кратковременное взаимодействие двух или более тел, возникающее в результате их соприкосновения. Например, столкновение шаров, удар молота о наковальню, попадание пули в мишень и т.д.
В качестве меры механического взаимодействия тел при ударе вместо ударной силы F служит ее импульс за время удара, т.е. величина
![]() = Fсрt,
= Fсрt,
где Fср— средняя сила удара,t— время удара.
Е сли
импульс за время удараtизменяется на конечную величину(m),
то из второго закона динамики получим
сли
импульс за время удараtизменяется на конечную величину(m),
то из второго закона динамики получим
Fсрt =(m). (1)
Измеряя время удара, можно определить из выражения (1) среднюю силу при ударе Fср.
Рассеяние механической энергии при ударе характеризуется коэффициентом восстановления скорости Кс,а также коэффициентом восстановления энергии Кэ. Коэффициент восстановления скорости определяется как отношение модуля скорости взаимного удаления центров тяжести тел после удара к модулю скорости их сближения до удара в проекции на общую нормаль к поверхности тел в точке их соприкосновения. Эта нормаль называетсялиниейудара(nnна рисунке 4).
Обозначим: А — точка контакта, О1, О2— центры тяжести тел,1nи2n– проекции на линию удара скоростей первого и второго тела до удара;u1nиu2n— проекции на линию удара тех же тел после удара. Тогда коэффициент восстановления скорости будет равен
u2n – u1n
Кс = (2)
2n – 1n
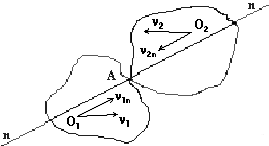
Рис.4
Коэффициент восстановления энергии зависит от системы отсчета. Он определяется как отношение суммарной кинетической энергии тел после удара Wк” к суммарной кинетической энергии тел до удара Wк’:
Кэ=Wк”/Wк’. (3)
Величины Кси Кэсвязаны между собой. Величина коэффициента восстановления зависит от физических свойств материалов соударяющихся тел, от их формы, а так же в сильной степени зависит от масс соударяющихся тел.
Для абсолютноупругогоудараКэ= 1, дляабсолютнонеупругогоудараКэ= 0, в реальных случаях 0 < Кэ < 1.
В настоящей работе рассматривается удар шаров, подвешенных в виде маятников, причем один шар до удара покоится (2= 0). Удар происходит в положении, соответствующем равновесию тел, и являетсяцентральнымипрямым. Это значит, что при ударе центры тяжести тел лежат на линии удара, а их относительная скорость параллельна линии удара.
Применяя к ударяющимся шарам закон сохранения импульса, можем написать:
для упругого удара
m11 = m1u1 + m2u2, (4а)
для абсолютно неупругого удара
m11 = (m1 + m2)u, (4б)
Здесь m1,m2– массы ударяющихся шаров;u1,u2– скорости шаров после упругого удара;u– скорость шаров после абсолютно неупругого удара.
При прямом центральном ударе, который рассматривается в данной работе, проекции скоростей тел на общую нормаль к их поверхностям в месте соударения совпадают с соответствующими скоростями тел: 1n = 1; u1n = u1 и т.д. Следовательно, выражение (2) для определения коэффициента восстановления скорости Кс переписывается в виде
u2 – u1
Кс = - (5)
2 – 1
Задания данной работы предусматривают проверку выражений закона сохранения импульса при упругом (4а) и абсолютно неупругом (4б) ударах и нахождение коэффициентов восстановления Кс и Кэ (3). Для выполнения этих заданий необходимо знать величины скоростей тел до и после соударения. Скорости шаров до и после удара можно определить, зная высоту, с которой тела начинают движение до удара, и высоту их подъема после удара. Без учета потерь энергии на преодоление сил сопротивления на основании закона сохранения энергии получаем:
для опускающегося шара
1
=
![]() ,
,
для поднимающихся шаров
u1
=
![]() и u2
=
и u2
=
![]() ,
,
где 1 – скорость первого шара до удара;
u1 и u2 – скорости шаров после соударения;
h1 – высота бросания первого шара, h1’ и h2’ – высоты поднятия шаров после соударения.
Поскольку на установке непосредственно измеряются углы, на которые отскакивают шары после удара, и угол бросания, скорость шаров будем определять из соотношений
1
= 2![]() sin(0/2);
u1
= 2
sin(0/2);
u1
= 2![]() sin(1/2);
u2
= 2
sin(1/2);
u2
= 2![]() sin(2/2),
(6)
sin(2/2),
(6)
где L — расстояние от точки подвеса до центра тяжести шаров, 0 — угол бросания, 1 и 2 — углы отскока первого и второго шаров.
