
Matematika / Математика. Сборник заданий, часть 1
.pdf
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«ЧЕРЕПОВЕЦКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Факультет общих математических и естественнонаучных дисциплин
Кафедра математики
МАТЕМАТИКА
Часть 1
ВВЕДЕНИЕ В ДИСКРЕТНУЮ МАТЕМАТИКУ
Учебно-методическое пособие
Череповец
2012
Рассмотрено на заседании кафедры математики, протокол № 10 от 22.05.12 г. Одобрено редакционно-издательской комиссией Факультета общих математи-
ческих и естественнонаучных дисциплин ЧГУ, протокол № 3 от 29.05.12 г.
Составители: Т.В. Гордобаева, Г.А. Киселёва, С.А. Парыгина, Н.В. Плотникова, И.А. Сенатова
Рецензенты: О.А. Кашинцева, канд. техн. наук, доцент (ЧГУ); В.А. Окунева, канд. физ.-мат. наук, доцент (ЧГУ)
Научный редактор: А.В. Толстиков, канд. физ.-мат. наук, проф.
© Коллектив авторов, 2012 © ФГБОУ ВПО «Череповецкий госу-
дарственный университет», 2012
2
Введение
Настоящее учебно-методическое пособие подготовлено для студентов первого курса различных направлений подготовки бакалавриата и специалитета. Пособие состоит из трех частей, охватывающих такие разделы дисциплины «Математика» как: «Введение в дискретную математику», «Линейная алгебра. Аналитическая геометрия» и «Введение в математический анализ. Дифференциальное и интегральное исчисление функции одной переменной».
Пособие предназначено для организации самостоятельной работы студентов по указанным разделам дисциплины «Математика» и рекомендуется для использования в рейтинговой оценке успеваемости студентов.
Часть 1 данного пособия «Введение в дискретную математику» состоит из двух тем: «Алгебра множеств» и «Алгебра высказываний». По теме «Алгебра множеств» студентам предлагаются задания на нахождение отношений между множествами, задание множеств различными способами, в том числе с помощью операций над множествами, а также наглядное представление множеств с помощью диаграмм Эйлера-Венна. По теме «Алгебра высказываний» – задания на доказательство справедливости равносильностей и законов логики.
3
1.АЛГЕБРА МНОЖЕСТВ
1.1Отношения между множествами
Задание 1.1.1. Определить отношения, которыми связаны следующие множества.
Номер |
Множества |
|
варианта |
||
|
||
|
|
|
1 |
2 |
|
|
|
|
1 |
А = {1, 3, 7, 9}, В = {1, 2, 3, 5, 7, 9, 10}, С = {3, 7}, |
|
D ={1, {3}, 7, 9} |
||
|
||
|
|
|
2 |
А = {2, 5, 8}, В = {1, 2, 4, 5, 7, 8, 9}, С = {8}, D = {8, 5, 2} |
|
|
|
|
3 |
А = {4, 5, 7, {8}}, В = {1, 2, 4, 5, 7, 8, 10}, С = {5, 7}, |
|
D = {4, 5, 7, 8} |
||
|
||
|
|
|
4 |
А = {3, 5, 7}, В = {2, 3, 5, 7, 8, 9, 10}, С = {7, 5, 3}, D = {{3}, 7, 5} |
|
|
|
|
5 |
А = {5, 3, 11, 9}, В = {1, 2, 3, 5, 7, 9, 11}, С = {3, 5}, |
|
D = {{3, 5}, 11, 9} |
||
|
||
|
|
|
6 |
А = {2, 4, 9}, В = {1, 2, 3, 4, 7, 9, 11}, С = {4}, D = {2, {4}, 9} |
|
|
|
|
7 |
А = {1, 2, 8, 9}, В = {1, 2, 3, 5, 7, 8, 9}, С = {2, 8}, |
|
D = {8, {1}, 2, 9} |
||
|
||
|
|
|
8 |
А = {1, 2, 7, 12}, В = {1, 2, 3, 5, 7, 9, 12}, С = {2, 1,7, 12}, |
|
D = {1, {2}} |
||
|
||
|
|
|
9 |
А = {5, 10, 8}, В = {1, 2, 5, 8, 9, 10}, С = {8}, D = {5, {8}, 10} |
|
|
|
|
10 |
А = {3, 8, 9}, В = {1, 2, 3, 5, 8, 9, 10}, С = {3, 9}, |
|
D = {{3}, 8, 9} |
||
|
||
|
|
|
11 |
А = {3, 7, 12}, В = {1, 2, 3, 5, 7, 9, 12}, С = {7, 3, 3}, |
|
D = {7, {12}, 3} |
||
|
||
|
|
|
12 |
А = {4, 5, 10, 8}, В = {1, 2, 4, 5, 8, 9, 10}, С = {8}, |
|
D = {5, {8}, 10, 4} |
||
|
||
|
|
|
13 |
А = {2, 8, 9, 11}, В = {1, 2, 5, 7, 8, 9, 11}, С = {2, 8}, |
|
D = {8, {11}, 2, 9} |
||
|
||
|
|
|
14 |
А = {1, 3, 9}, В = {1, 2, 3, 5, 7, 9, 10, 11}, С = {3, 1, 9}, |
|
D = {{3}, 1, 9} |
||
|
||
|
|
|
15 |
А = {2, 7, {8}}, В = {1, 2, 4, 5, 7, 8, 10}, С = {2, 7}, D = {2, 7, 8} |
|
|
|
|
16 |
А = {-1, 0, 5}, В = {-1, 0, 3, 4, 5, 7}, С = {-1, 0, 2, 5, {7}}, D = {7} |
|
|
|
4
|
Окончание |
|
|
1 |
2 |
|
|
17 |
А = {4, 6}, В = {4, 5, {6}, 7}, С = {-3, 0, 2, 3, 4, 5, 6, 7}, |
|
D = {4, 5, 6, 7} |
18 |
А = {0, 3, 5, 8, 9}, В = {8, 5, {0}, 3, 9}, С = {-1, 0, 3, 4, 5, 7, 8, 9}, |
|
D = {{0}} |
19 |
А = {{2, 8}}, В = {1, 5, 2, 4, 6, 7, 8}, С = {2, 8}, D = {2} |
|
|
20 |
А = {-4, -2, 0, 4, 6}, В = {6, 0, 4}, С = {4}, D = {{4}, 6, 0} |
|
|
21 |
А = {3, 2, 1}, В = {-4, -1, 1, 2, 3, 5, 7, 9}, С = {3}, D = {{3}, 1, 2} |
|
|
22 |
А = {-1}, В = {0, 2, 4, 6, -3, -6, -1}, С = {-1, 5, 2}, D = {{-1}, 2, 5} |
|
|
23 |
А = {0, 3, 8}, В = {-1, 0, 1, 2, 3, 4, 7, 8}, С = {3, 0, 8}, D = {{0}} |
|
|
24 |
А = {1, 2, 3, 5, 7, 9}, В = {7, 2, 5}, С = {2, 7}, D = {{5}, 2, 7} |
|
|
25 |
А = {-1, 5}, В = {-2, -1, 0, 2, 4, 5, 8}, С = {{5, -1}}, D = {-1} |
|
|
26 |
А = {-2, -1, 0, 3, 4, 5, 8}, В = {{8, -2}}, С = {0, -2, 4, 8}, D = {-2, 8} |
|
|
27 |
А = {5, 8, 10}, В = {1, 2, 3, 5, 8, 9, 10}, С = {5, 5, 8}, D = {8, {10}, 5} |
|
|
28 |
А = {{4, 1}}, В = {1, 5, 2, 4, 6, 7, 8}, С = {1, 4}, D = {4} |
|
|
29 |
А = {0, 6, 2, 8}, В = {0, 2, 3, 6, 7, 8, 10}, С = {6, 8}, D = {6, {0}, 2, 8} |
|
|
30 |
А = {2, 4, 7, 10}, В = {1, 2, 4, 5, 7, 9, 10}, С = {4, 2}, |
|
D = {{4, 2}, 10, 7} |
Образец выполнения задания 1.1.1.
Определить отношения, которыми связаны следующие множе-
ства: А = {0, 2, 8, 10}, В = {0, 1, 2, 4, 5, 8, 9, 10, 11}, С = {2}, D = {8, {2}, 10, 0}.
Р е ш е н и е.
Два множества А и В могут быть связаны следующими отношениями: А = В (множество А равно множеству В), А В (множество А включено во множество В) и А В (множество А строго включено во множество В).
Таким образом, необходимо для каждой пары исходных множеств А, В, С, D указать то отношение, которое связывает их наилучшим образом (в смысле выполнения соответствующих определений).
5
Тогда имеем следующие отношения между исходными множествами:
1)А В (каждый элемент множества А принадлежит множеству
Ви во множестве В есть элементы, не принадлежащие множеству
А);
2)С В (единственный элемент множества С, являющийся числом 2, принадлежит множеству В и во множестве В есть элементы, не принадлежащие множеству С);
3)С А (элемент множества С принадлежит множеству А и во множестве А есть элементы, не принадлежащие множеству С).
Отношения между множествами, которые мы нашли, в данном примере образуют цепочку: С А В .
Так как множеству D принадлежит элемент {2}, который по своей математической природе представляет собой множество, состоящее из числа 2, а ни в одном из множеств А, В, С такого элемента нет (каждому из этих множеств принадлежит элемент, представляющий собой просто число 2), то множество D не связано никакими отношениями со множествами А, В и С.
О т в е т: А В , С В , С А или С А В .
|
|
1.2 Операции над множествами |
|
|
|
|
|
|
|||
|
Задание 1.2.1. Найти множества (A È B)\(A Ç B), |
|
, |
|
и изо- |
||||||
А |
В |
||||||||||
бразить их на диаграммах Эйлера-Венна. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||
|
Номер |
|
Множества А и В |
Универсальное |
|
||||||
|
варианта |
|
множество U |
|
|||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
2 |
|
3 |
|
|
|||
|
|
|
|
|
|
|
|
||||
|
1 |
A = {x| x Z, |
– 2 |
≤ x < 2}, |
|
U = {x| x Z, |
|
||||
|
B = {x| x = 2n – 3, |
n N, |
n ≤ 4} |
x [– 4, 7]} |
|
||||||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||
|
2 |
A = {x| x Z, |
– 3 |
≤ x < 0}, |
|
U = {x| x Z, |
|
||||
|
B = {x| x = – 2n +1, n N, |
n ≤ 5} |
x [– 11, 0]} |
|
|||||||
|
|
|
|||||||||
|
|
|
|
|
|
||||||
|
3 |
A = {x| x = 3n +1, |
n N, n < 5}, |
U = {x| x Z, |
|
||||||
|
B = {x| x Z, |
5 < x < 12} |
|
x [2, 14]} |
|
||||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
6
|
|
|
|
|
Продолжение |
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
4 |
A = {x| x = n – 2, |
n N, |
n ≤ 5}, |
U = {x| x Z, |
|
|
B = {x| x Z, |
– 2 |
≤ x ≤ 1} |
x [– 4, 5]} |
|
||
|
|
|||||
|
|
|
|
|
||
5 |
A = {x| x = n + 3, |
n N, 3 ≤ n < 7}, |
U = {x| x Z, |
|
||
B = {x| x Z, |
5 ≤ x ≤ 8} |
|
x [2, 11]} |
|
||
|
|
|
||||
|
|
|
|
|
||
6 |
A = {x| x Z, |
3 ≤ x < 10}, |
U = {x| x Z, |
|
||
B = {x| x = 2n+1, n N, n < 4} |
x [2, 17]} |
|
||||
|
|
|||||
7 |
A = {x| x = 2n – 1, |
n N, 2 ≤ n ≤ 4}, |
U = {x| x Z, |
|
||
B = {x| x Z, |
4 < x ≤ 9} |
|
x [1, 10]} |
|
||
|
|
|
||||
|
|
|
|
|
|
|
8 |
A = {x| x = 3n – 2, |
n N, |
n ≤ 3}, |
U = {x| x Z, |
|
|
B = {x| x Z, |
1 < x ≤ 4} |
|
x [0, 10]} |
|
||
|
|
|
||||
|
|
|
|
|
|
|
9 |
A = {x| x = n – 4, |
n N, |
n ≤ 5}, |
U = {x| x Z, |
|
|
B = {x| x Z, |
– 3 < x ≤ 3} |
x [– 4, 6]} |
|
|||
|
|
|||||
|
|
|
|
|
|
|
10 |
A = {x| x =5n – 4, |
n N, |
n ≤ 3}, |
U = {x| x Z, |
|
|
B = {x| x Z, |
0 ≤ x ≤ 6} |
|
x [– 1, 12]} |
|
||
|
|
|
||||
|
|
|
|
|||
11 |
A = {x| x =4 – n , n N, n ≤ 3}, |
U = {x| x Z, |
|
|||
B = {x| x Z, |
–3 |
≤ x < 1} |
|
x [– 5, 6]} |
|
|
|
|
|
||||
|
|
|
|
|
|
|
12 |
A = {x| x = n2 |
– 5, |
n N, |
n < 5}, |
U = {x| x Z, |
|
B = {x| x Z, |
–2 |
≤ x < 5} |
|
x [– 5, 12]} |
|
|
|
|
|
||||
|
|
|
|
|
|
|
13 |
A = {x| x Z, |
1 < x ≤ 6}, |
|
U = {x| x Z, |
|
|
B = {x| x = 2n, |
n N, n ≤ 2} |
x [– 2, 8]} |
|
|||
|
|
|||||
14 |
A = {x| x =2n – 7, |
n N, |
n ≤ 4}, |
U = {x| x Z, |
|
|
B = {x| x Z, |
– 2 |
≤ x < 2} |
x [– 6, 4]} |
|
||
|
|
|||||
|
|
|
|
|
|
|
15 |
A = {x| x = n2 |
+ 1, |
n N, |
n < 4}, |
U = {x| x Z, |
|
B = {x| x Z, |
2 ≤ x < 6} |
|
x [1, 11]} |
|
||
|
|
|
||||
|
|
|
|
|||
16 |
A = {x| x = – 5n + 10, n N, 2 ≤ n < 5}, |
U = {x| x Z, |
|
|||
B = {x| x Z, |
– 10 |
≤ x < – 4} |
x [– 12, 1]} |
|
||
|
|
|||||
|
|
|
|
|||
17 |
A = {x| x = – 2n + 5, n N, n ≤ 5}, |
U = {x| x Z, |
|
|||
B = {x| x Z, |
– 4 |
≤ x < 2} |
x [– 7, 6]} |
|
||
|
|
|||||
|
|
|
|
|
|
|
18 |
A = {x| x Z, |
0 ≤ x ≤ 5}, |
|
U = {x| x Z, |
|
|
B = {x| x = 3n – 5, |
n N, |
n < 6} |
x [– 3, 11]} |
|
||
|
|
|||||
|
|
|
|
|
||
19 |
A = {x| x = (n – 2 )2, n N, |
3 ≤ n < 6}, |
U = {x| x Z, |
|
||
B = {x| x Z, |
3 < x ≤ 10} |
x [0, 12]} |
|
|||
|
|
|||||
|
|
|
|
|
||
20 |
A = {x| x = 1 – 2 n, |
n N, 3 ≤ n < 7}, |
U = {x| x Z, |
|
||
B = {x| x Z, |
– 12 ≤ x < – 6 } |
x [– 14, – 4]} |
|
|||
|
|
|||||
|
|
|
|
|
|
|
7

|
|
|
|
|
Окончание |
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
3 |
|
|
|
|
|
|
||
21 |
A = {x| x = 4 – 3 n, |
n N, 1 < n < 5}, |
U = {x| x Z, |
|
||
B = {x| x Z, |
– 10 ≤ x < – 4 } |
x [– 11, 0]} |
|
|||
|
|
|||||
|
|
|
|
|
|
|
22 |
A = {x| x Z, |
2 ≤ x < 9}, |
|
U = {x| x Z, |
|
|
B = {x| x = 2n + 2, |
n N, n ≤ 4} |
x [1, 12]} |
|
|||
|
|
|||||
|
|
|
|
|
|
|
23 |
A = {x| x Z, |
– 6 |
< x ≤ – 3}, |
|
U = {x| x Z, |
|
B = {x| x = – n – 3, |
n N, |
n ≤ 5} |
x [– 9, – 2]} |
|
||
|
|
|||||
|
|
|
|
|
||
24 |
A = {x| x = – 5 |
+ n, n N, 5 < n ≤ 9}, |
U = {x| x Z, |
|
||
B = {x| x Z, |
– 1 |
≤ x < 4} |
|
x [– 3, 5]} |
|
|
|
|
|
||||
|
|
|
|
|
|
|
25 |
A = {x| x Z, |
0 < x ≤ 5}, |
|
U = {x| x Z, |
|
|
B = {x| x = – 2 + 2n, n N, |
n < 4} |
x [– 1, 7]} |
|
|||
|
|
|||||
|
|
|
|
|
|
|
26 |
A = {x| x Z, |
0 ≤ x ≤ 5}, |
|
U = {x| x Z, |
|
|
B = {x| x = – 4 + 2 n, n N, 3 ≤ n < 6} |
x [– 2, 8]} |
|
||||
|
|
|||||
|
|
|
|
|
||
27 |
A = {x| x = – 3 n +3, n N, |
n ≤ 4}, |
U = {x| x Z, |
|
||
B = {x| x Z, |
– 7 |
≤ x < – 1} |
|
x [– 10, 1]} |
|
|
|
|
|
||||
|
|
|
|
|
|
|
28 |
A = {x| x Z, |
3 < x ≤ 8}, |
|
U = {x| x Z, |
|
|
B = {x| x = (n + 1)2, n N, |
n ≤ 2} |
x [0, 10]} |
|
|||
|
|
|||||
29 |
A = {x| x =5n – 3, |
n N, n < 4}, |
U = {x| x Z, |
|
||
B = {x| x Z, |
6 < x ≤ 13} |
|
x [1, 14]} |
|
||
|
|
|
||||
|
|
|
|
|
|
|
30 |
A = {x| x Z, |
– 4 < x ≤ 4}, |
|
U = {x| x Z, |
|
|
B = {x| x = – n + 2, n N, |
n ≤ 3} |
x [– 5, 5]} |
|
|||
|
|
|||||
|
|
|
|
|
|
|
Образец выполнения задания 1.2.1.
Найти множества (A È B) \ (A Ç B), А , В и изобразить их на диаграммах Эйлера-Венна, если A = {x| x Z, – 12 ≤ x < – 5},
B = {x| x =1 – 4 n, n N, n < 5}, U = {x| x Z, x [– 16, – 1]}.
Р е ш е н и е.
Множество А = {x| x Z, – 12 ≤ x < – 5} задано указанием характеристического свойства, перечислим его элементы:
A = {– 12, – 11, – 10, – 9, – 8, – 7, – 6}.
8
Множество В = {x| x =1 – 4 n, n N, n < 5} задано с помощью порождающей процедуры, найдем его элементы. Начальный набор значений параметра n определяется условиями, что n – это натуральное число, меньшее пяти. Учитывая, что наименьшее натуральное число – это 1, получим: n = 1, 2, 3, 4. Тогда:
− |
при n = 1, находим x = 1 – 4 |
· 1 |
= – 3; |
− |
при n = 2, находим x = 1 – 4 |
· 2 |
= – 7; |
− |
при n = 3, находим x = 1 – 4 |
· 3 |
= – 11; |
− |
при n = 4, находим x = 1 – 4 |
· 4 |
= – 15. |
Перечислим элементы множества В:
В = {– 15, – 11, – 7, – 3}.
Универсальное множество U = {x| x Z, x [– 16, – 1]} задано указанием характеристического свойства, перечислим его элементы:
U = {– 16, – 15, – 14, – 13, – 12, – 11, – 10, – 9, – 8 |
, – 7, – 6, – 5, |
– 4, – 3, – 2, – 1}. |
|
Далее, зная элементы каждого из множеств А и В, найдем элементы множеств A È B (объединение множеств А и В) и A Ç B (пересечение множеств А и В), опираясь на соответствующие определения операций объединения и пересечения множеств.
Тогда получим:
A È B = {– 15, – 12, – 11, – 10, – 9, – 8, – 7, – 6, – 3},
A Ç B = {– 11, – 7}.
Отсюда найдем разность множеств A È B и A Ç B, опираясь на соответствующее определение операции разности, тем самым получим искомое множество (A È B)\(A Ç B):
(A È B) \ (A Ç B) = {– 15, – 12, – 10, – 9, – 8, – 6, – 3}.
9
Множества А и В найдем, используя определение операции отрицания множеств, в соответствии с которым
|
|
А = U \ A = {– 16, – 15, – 14, – 13, – 5, – 4, – 3, – 2, – 1} |
, |
|
|
|
= U \ B ={– 16, – 14, – 13, – 12, – 10, – 9, – 8, – 6, – 5, |
– 4, – 2, –1}. |
|
В |
||||
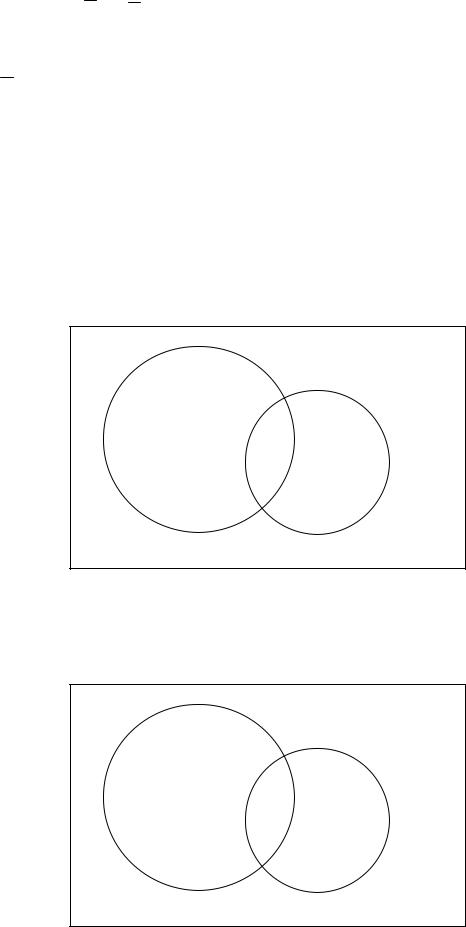
Изобразим полученные множества на диаграммах ЭйлераВенна.
I. Множество (A È B) \ (A Ç B) будем изображать по действиям. 1. Диаграмма Эйлера-Венна для множества A È B:
A
|
.-12 |
|
|
.-9 |
|
.-10 |
.-7 |
.-15 |
|
|
|
|
.-11 |
|
.-8 |
.-6 |
.-3 |
|
|
U
B
A È B
2. Диаграмма Эйлера-Венна для множества A Ç B:
U
A
|
.-12 |
|
|
.-9 |
|
.-10 |
.-7 |
.-15 |
|
|
|
|
.-11 |
|
B
.-8 |
.-6 |
.-3 |
|
|
A Ç B
10
