Итерация 2.

Выбираем узел 2 как базовый, т.е. проверяем, приведет ли его использование к более коротким цепям. Вычеркиваем в матрице D₁ вторую строку и второй столбец. Вычеркиваем также столбцы 6,7,8, так как они содержат элементы, равные , принадлежащие базовой строке, и строки 6,7,8, так как они содержат элементы, равные , принадлежащие базовому столбцу. Исключаем также диагональные элементы. Остается исследовать элементы (1,3); (1,4); (1,5); (3,1); (3,4); (3,5); (4,1); (4,3); (4,5); (5,1); (5,3); (5,4). Здесь улучшены могут быть только оценки d¹₁₃, d¹₁₅, d¹₃₁, d¹₄₅, d¹₅₁, d¹₅₄, равные .

d²₁₃=min[d¹₁₃; d¹₁₂+d¹₂₃]=min[;9+2]=11;

d²₃₁=min[d¹_31; d¹₃₂+d¹₂₁]=min[;2+9]=11;

d²₁₅=min[d¹₁₅; d¹₁₂+d¹₂₅]=min[;9+7]=16;

. . .

Таким образом, r²₁₃ = r²₃₁ = r²₁₅ = r²₄₅ = r²₅₁ = r²₅₄ =2; остальные элементы r²_ij остаются без изменений. Новые матрицы имеют вид:

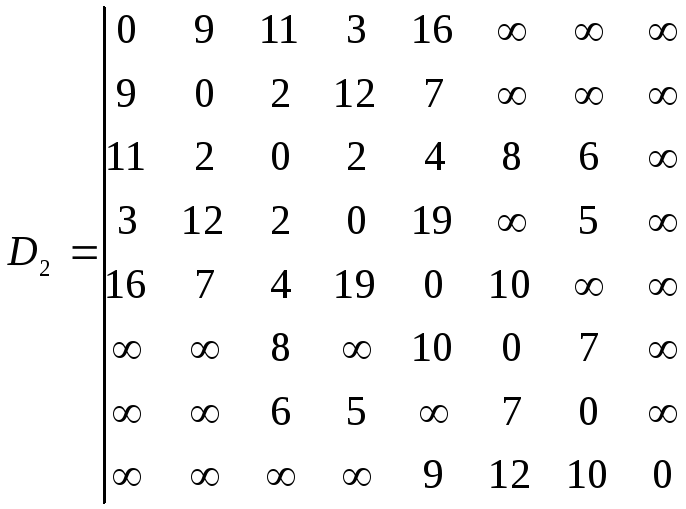
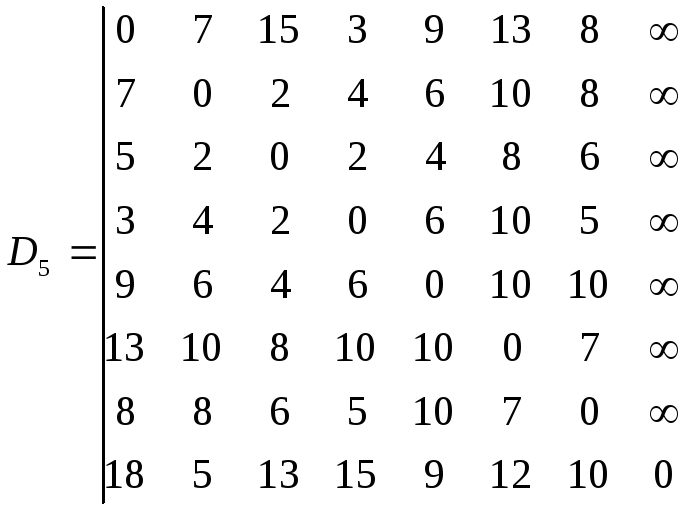
Аналогично получаем матрицы D_j и R_j, j = 3,…,8. Матрицы D_j и R_j, j=5,6,7,8, остаются без изменений. Следовательно, оптимальное решение соответствует матрицам D₅ и R₅, определяющим и оптимальное расстояние для передачи между объектами, и последовательность передачи информации.

Алгоритм «Приписывания меток»

На первом этапе последовательно приписываются метки вершинам исходного графа до тех пор, пока не будет помечена искомая вершина. На втором этапе по приписанным меткам восстанавливается искомый путь.

Пусть задан граф, у которого дуги (рёбра) не взвешены и вершины пронумерованы индексом . Требуется найти кратчайший путь из вершины  в вершину , т.е. путь , состоящий из наименьшего числа дуг. Через  обозначим множество всех вершин, в которые исходят дуги из вершины .

Этап 1. На нулевом шаге вершине  приписываем метку . На первом шаге всем вершинам  приписываем метки . На каждом последующем шаге  действуем следующим образом: если вершина  помечена меткой , то всем еще непомеченным вершинам  приписываем метку . Этап 1 заканчивается на некотором шаге , как только вершина  окажется отмеченной меткой .

Этап 2. Коль вершина  помечена меткой , то кратчайший путь  состоит из  дуг, причем, у каждой из этих дуг  метка начала  на единицу меньше метки конца : . Тогда для нахождения  достаточно проследовать от вершины  к вершине  с меткой , от вершины  к вершине  с меткой  и т.д., пока не дойдем до вершины . Если вершин с одинаковой меткой несколько, то выбирается любая.

Алгоритм «Ветвей и границ»

Метод ветвей и границ (англ. branch and bound) — общий алгоритмический метод для нахождения оптимальных решений различных задач оптимизации, особенно дискретной и комбинаторной оптимизации. По существу, метод является вариацией полного перебора с отсевом подмножеств допустимых решений, заведомо не содержащих оптимальных решений.

Метод ветвей и границ был впервые предложен Ленд и Дойг в 1960 г. для решения задач целочисленного программирования.