3. Задание

Используя задачу лабораторной работы на тему «Решение ЗЛП симплекс-методом» согласно варианту как прямую задачу, требуется:

3.1. Сформулировать в экономических терминах двойственную задачу и составить ее математическую модель;

3.2. Используя решение исходной задачи и соответствие между двойственными переменными, найти компоненты оптимального плана двойственной задачи – двойственные оценки.

3.3. Указать наиболее дефицитный и недефицитный ресурс, если он имеется.

3.4. С помощью двойственных оценок обосновать рациональность оптимального плана, сопоставив оценку затрат израсходованных ресурсов и максимальный доход от реализации продукции по всему оптимальному плану и по каждому виду продукции в отдельности.

Тема: Решение транспортных задач

1. Цель работы

2. Закрепить знания построения математической модели транспортной задачи

3. Научится строить первый опорный план задачи методов наименьших тарифов

4. Научится находить оптимальное решение задачи методом потенциалов

2. Теоретические сведения

Под термином «транспортные задачи» понимается широкий круг задач не только транспортного характера. Общим для всех этих задач, как правило, распределение ресурсов находящихся у m производителей (поставщиков), по n потребителям этих ресурсов. К наиболее часто встречаются следующие транспортные задачи:

• Прикрепление потребителей ресурса к производителям;

• Привязка пунктов отправления к пунктам назначения;

• Взаимная привязка грузопотоков прямого и обратного направления;

• Некоторые задачи оптимальной загрузки оборудования;

• Оптимальное распределение объемов выпуска между заводами –изготовителями;

• Распределение по должностям и др.

1. Постановка задачи и ее математическая модель

Имеется m пунктов отправления (поставщиков) грузов :

А₁, А₂, А₃,…. ,А_i,….., А_m,

на которых сосредоточены запасы какого-либо однородного груза в объемах соответственно :

а₁, а₂, а₃,…. ,а_i,….., а_m.

Величина а_i определяет максимально возможные размеры поставок грузов из пунктов отправления. Суммарный запас груза у поставщиков составляет

_m

 а_i

ⁱ

Кроме того, имеются n пунктов назначения (получателей):

В₁, В₂, В₃,…. ,В_j,….., В_n,

которые подали заявки на грузы в объемах соответственно:

b₁, b₂, b₃,…. ,b_j,….., b_n.

_n

Суммарная величина заявок составляет b_j .

^j

Стоимость перевозок одной единицы груза от поставщика А_i к потребителю В_j обозначим через C_ij (транспортный тариф) и составим матрицу транспортных издержек. В качестве критерия оптимальности выбираем суммарные издержки по перевозке грузов.

Тогда транспортная задача формулируется таким образом:

Необходимо составить оптимальный план т.е. найти такие значения объемов перевозок грузов (х_ij)от поставщиков А_i к потребителям В_j, чтобы вывести все от поставщиков, удовлетворить заявки потребителей и обеспечить минимальные транспортные расходы на перевозку груза. Все исходные данные транспортной задачи можно записать в виде таблицы, которую называют транспортной. Тарифы пишем в правом верхнем углу, распределенные грузы в середине клетки

Пункты отправления	Пункты назначения						Запасы ai
	В1	В2	…..	Вj	….	Вn
A1	C11 X11	C12 X12		C1j X1j		C1n X1n	a1
A2	C21 X21	C22 X22		C2j X2j		C2n X2n	A2
Ai	Ci1 Xi1	Ci2 Xi2		Cij Xij		Cin Xin	Ai
Am	Cm1 Xm1	Cm2 Xm2		Cmj Xmj		Cmn Xmn	Am
Заявки bj	b1	B2		bj		bn

Математическая постановка транспортной задачи заключается в определении плана перевозок (матрица Х), который удовлетворяет следующим условиям

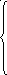_n

 x_ij = a_i i=(1 2 …m) ( сумма по строчкам)

^j=1

_m

 x_ij = b_j j=(1 2 …n) (сумма по столбикам)

ⁱ⁼¹

x_ij>=0 j=(1 2 …n) i=(1 2 …m)

и обеспечивает минимальное значение целевой функции

_{m n}

F(X)=   c_ij x_ij min

^{I=1 j=1}

В рассмотренной модели предполагается, что суммарные запасы равны суммарным потребностям т.е.

_{m n}

 a_i =  b_j

^{i=1 j=1}

Такая модель называется закрытой. А любая транспортная задачи, у которой суммарный запас совпадает с суммарными потребностями, имеет решение. Если это условие не соблюдается, модель называется открытой.

В этом случае вводят или фиктивного пункт назначения (если запасы превышают заявки), или фиктивного отправления (если заявки превышают запасы). И получают закрытую модель. Соответствующие тарифы фиктивных пунктов считаются равными нулю.