Тема: Решение двойственных задач линейного программирования

1.Цель работы

1. Изучить теоретический материал по решению двойственных задач линейного программирования.

2. Научиться записывать математическую модель для двойственной задачи линейного программирования.

3. Изучить методы решения двойственных задач линейного программирования.

2. Теоретические сведения

Любой задаче линейного программирования можно поставить в соответствие другую задачу, сформули­рованную по стандартным правилам таким образом, что решение любой из них является и решением другой задачи. Такие задачи на­зываются взаимодвойственными.

2.1 ПОСТРОЕНИЕ ДВОЙСТВЕННОЙ ЗАДАЧИ

Двойственная обратная задача — задача линейного программи­рования, формулируемая с помощью определенных правил непо­средственно из условий исходной, или прямой задачи. В литерату­ре по линейному программированию в большинстве случаев рас­сматриваются формулировки двойственной задачи, соответствую­щие различным формам прямой задачи, которые, в свою очередь, определяются типом ограничений, знаками переменных и направ­лением оптимизации (максимизация или минимизация). Опыт по­казывает, что на начальной стадии изучения теории линейного про­граммирования детали различных формулировок двойственной за­дачи нередко затрудняют восприятие материала.

Рассмотрим обобщенную формулировку двойственной зада­чи линейного программирования, которая применима к любой форме представления прямой задачи. В основу такой формули­ровки положен тот факт, что использование симплекс-метода тре­бует приведения любой задачи линейного программирования к стандартной форме. Так как все методы вычислений, основан­ные на соотношениях двойственности, предполагают непосред­ственное использование симплекс-таблиц, формулировка двой­ственной задачи в соответствии со стандартной формой прямой задачи представляется достаточно логичной. Следует, однако, помнить, что приводимая ниже формулировка двойственной задачи является обобщенной в том смысле, что она применима ко всем формам прямой задачи.

Прямая задача линейного программирования в стандартной форме записывается следующим образом:

максимизировать

п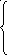ри ограничениях:

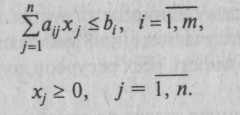
Чтобы сформулировать условия двойственной задачи, проведем симметричное структурное преобразование условий прямой задачи в соответствии со следующими правилами:

1. каждому ограничению прямой задачи соответствует переменная двойственной задачи;

2. каждой переменной прямой задачи соответствует ограниче­ние двойственной задачи;

3. коэффициенты при некоторой переменной, фигурирующие в ограничениях прямой задачи, становятся коэффициентами левой части соответствующего ограничения двойственной задачи, а коэффициент, фигурирующий при той же переменной в выражении для целевой функции прямой задачи, становится постоянной пра­вой части этого же ограничения двойственной задачи.

На примере задачи планирования товарооборота двойственная задача формулируется следующим образом:

определить оценку (неявную стоимость) единицы каждого вида ресурсов y_j (i=1,m), чтобы при заданных объемах ресурсов b_i, при­были c_j, нормах расхода ресурсов a_ij минимизировать оценку всех ресурсов торгового предприятия, затраченных на организацию тор­гового процесса.

Запишем математическую модель двойственной задачи:

Определить вектор Y= (у_ь у₂, ..., у_т), который удовлетворяет ограничениям

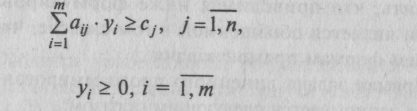
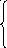
обеспечивает минимальное значение целевой функции

Ограничения по переменным y_i показывают, что стоимость всех ресурсов, затраченных на продажу единицы j группы товаров, должна быть не меньше дохода, получаемого при реализации единицы у группы товаров, а общая стоимость всех ресурсов должна быть минимизи­рована.

В целом двойственная задача по отношению к исходной состав­ляется согласно следующим правилам:

1. Число переменных в двойственной задаче равно числу ограни­чений в прямой задаче.

2. Матрица коэффициентов системы ограничений двойственной задачи получается из матрицы коэффициентов системы ограни­чений прямой задачи путем транспонирования.

3. Система ограничений двойственной задачи записывается в виде неравенств противоположного смысла неравенствам системы ограничений прямой задачи.

4. Свободными членами системы ограничений двойственной зада­чи являются коэффициенты функции цели прямой задачи.

5. Двойственная задача решается на минимум, если целевая функция прямой задачи задается на максимум, и наоборот.

6. Коэффициентами функции цели двойственной задачи служат свободные члены системы ограничений прямой задачи.

7. Если переменная прямой задачи х_j >=0, то j-е условие системы ограничений двойственной задачи является неравенством, если x_j — любое число, то j-е условие двойственной задачи представ­ляет собой уравнение.

8. Если i-е соотношение прямой задачи является неравенством, то соответствующая оценка i-го ресурса — переменная y_i >=0, если i-е соотношение представляет собой уравнение, то переменная двойственной задачи у_i — любое число.

Решение прямой задачи дает оптимальные объемы в структуре товарооборота торгового предприятия, а решение двойственной — оптимальную систему оценок ресурсов, используемых для реализа­ции товаров.

Если найти оптимальный план прямой задачи, то можно получить оптимальный план двойственной задачи.

Установим соответствие между переменными прямой и двойст­венной задач в симплексной таблице 1.

Таблица 1 – Соотношения переменных

Переменные прямой задачи (заголовок симплексной таблицы)	Переменные двойственной задачи (их значения расположены в индексной строке оптимальной симплексной таблицы)
основные x1, x2, …, xn	дополнительные ym+1, ym+2, …, ym+n
дополнительные xn+1, xn+2, …, xn+m	основные y1, y2, … , ym

Согласно сопряженным парам переменных из решения прямой задачи, можно получить решение двойственной, не решая ее, и на­оборот, из решения двойственной задачи - решение прямой.

2.2 ПРИМЕР РЕШЕНИЯ ДВОЙСТВЕННОЙ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Условие задачи. Коммерческое предприятие, располагающее матери­ально-денежными ресурсами, реализует три группы товаров А, В и С. Плановые нормативы затрат ресурсов на 1 тыс. руб. товарообо­рота, доход от продажи товаров на 1 тыс. руб. товарооборота, а также объем ресурсов заданы в таблице 2.

Определите плановый объем продажи и структуру товарообо­рота так, чтобы доход торгового предприятия был максимальный.

Таблица 2– Плановые нормативы

Виды материально-денежных ресурсов	Норма затрат материально-денежных ресурсов на 1 тыс руб товарооборота			Объем ресурсов bi
	Группа А	Группа В	Группа С
Рабочее время продавцов, чел-ч	0,1	0,2	0,4	1100
Площадь торговых залов, м2	0,05	0,02	0,02	120
Площадь складских помещений, м2	3	1	2	8000
Доход, тыс руб	3	5	4	Max

Решение. Запишем математическую модель задачи.

Определим вектор X= (x₁, х₂, х₃), который удовлетворяет усло­виям

0,1х₁ + 0,2х₂ + 0,4*х₃<=1100

0,05х₁ + 0,02х₂ + 0,02х₃ <= 120

Зх₁ +х₂ + 2х₃ <= 8000

х₁ > =0, х₂ > =0, х₃ >=0

и обеспечивает максимальное значение целевой функции

F(X) = 3х₁ + 5х₂ + 4х₃ -> max.

Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных х₄, х₅, х₆:

0,1х₁ + 0,2х₂ + 0,4х₃ + х₄ ⁼ 1100

0,05х₁ + 0,02х₂ + 0,02х₃+х₅=120

Зх₁ + х₂ + 2х₃ + х₆ = 8000.

Решим систему уравнений относительно базисных переменных.

х₄ = 1100 - (0,1х₁ + 0,2х₂ + 0,4х₃),

х₅ = 120 - (0,05х₁ + 0,02х₂ + 0,02х₃),

х₆ = 8000 - (Зх₁ + х₂ +3х₃).

Функцию цели запишем в виде уравнения:

F(Х) = 0 - (-Зх₁ - 5х₂ - 4х₃).

Полагая, что свободные переменные х₁ = 0, х₂ = 0, х₃ = 0, полу­чим первый опорный план X₁= (0, 0, 0, 1100, 120, 8000), F(X₁) = 0, в котором базисные переменные х₄ = 1100,х₅ = 120, х₆ =8000. Сле­довательно, товары не продаются, доход равен нулю, а ресурсы не используются. Полученный первый опорный план запишем в симп­лексную таблицу 3.

Таблица 3 – Симплексная таблица

План	Базисные переменные	Значения базисных переменных	Значения коэффициентов при переменных						δi
			Х1	Х2	Х3	Х4	Х5	Х6
I	Х4 Х5 Х6	1100 120 8000	0,1 0,05 3	0,2 0,02 1	0,4 0,02 2	1 0 0	0 1 0	0 0 1	5500 6000 8000
Индексная строка	F(X1)	0	-3	-5	-4	0	0	0
II	X2 X5 X6	5500 10 2500	0,5 0,04 2,5	1 0 0	2 -0,02 0	5 -0,1 -5	0 1 0	0 0 1	11000 250 1000
Индексная строка	F(X2)	27500	-0,5	0	6	25	0	0
III	Х2 Х1 Х6	5375 250 1875	0 1 0	1 0 0	2,25 -0,5 1,25	6,25 -2,5 1,25	12,5 25 -62,5	0 0 1
Индексная строка	F(X3)	27625	0	0	5,75	23,75	12,5	0

На третьей итерации таблицы 2 получаем план III, который явля­ется оптимальным, так как все коэффициенты в индексной строке >=0.

Оптимальный план можно записать так:

X = (250, 5375, 0, 0, 0, 1875), F(Х) = 27 625 тыс. руб.

Следовательно, необходимо продавать товаров первой группы А – 250 ед., а второй группы В — 5375 ед. При этом торговое предпри­ятие получает максимальный доход в размере 27 625 тыс. руб. То­вары группы С не реализуются.

В оптимальном плане среди базисных переменных находится дополнительная переменная х₆. Это указывает на то, что ресурсы третьего вида (площадь складских помещений) недоиспользована на 1875 м², так как переменная х₆ была введена в третье ограниче­ние задачи, характеризующее собой использование складских по­мещений этого ресурса.

Составим двойственную задачу к прямой задаче планирования товарооборота, которая решена симплексным методом.

Прямая задача	Двойственная задача
Х=(х1, х2, х3) при 0,1х1+0,2х2+0,4х3<=1100 0,05х1+0,02х2+0,02х3<=120 3х1+х2+2х3<=8000 х1, х2, х3>=0 F(X)=3x1+5x2+4x3 –> max	Y=(y1, y2, y3) при 0,1у1+0,05у2+3у3>=3 0,2у1+0,02у2+у3>=5 0,4у1+0,02у2+2у3>=4 у1, у2, у3 >=0 Z(Y)=1100y1+120y2+8000y3 –> min

Задачи образуют симметрическую пару двойственных задач. Решение прямой задачи дает оптимальный план товарооборота по реализации трех групп товаров, а решение двойственной — опти­мальную систему оценок ресурсов, используемых в процессе реа­лизации.

Решение прямой задачи получено симплексным методом. Оп­тимальный план товарооборота:

X = (250; 5375; 0; 0; 0; 1875); F(X) = 27 625 тыс. руб.

Используя последнюю итерацию прямой задачи (план III симп­лексной таблицы 2), найдем оптимальный план двойственной зада­чи.

Оптимальный план двойственной задачи равен:

Y= (23,75; 12,5; 0; 0; 0; 5,75); Z(Y) = 27 625.

Подставим оптимальный план прямой задачи в систему огра­ниченной математической модели планирования товарооборота:

0,1 * 250 + 0,2 * 5375 + 0,4 * 0 = 1100;

0.05 * 250 + 0,02 * 5375 + 0,02 * 0 = 120;

3 * 250 + 1 * 5375 + 2 * 0 < 8000.

Первое и второе ограничение прямой задачи выполняются как равенства. Это означает, что ресурсы первого и второго видов пол­ностью используются в оптимальном плане, являются дефицитны­ми и их оценки отличны от нуля (у₁ > 0, у₂ > 0). Третье ограничение выполняется как стро­гое неравенство, т. е. ресурс третьего вида израсходован не полно­стью, остаток его в оптимальном плане х₆* = 1875. Значит, ресурс третьего вида не является дефицитным и цены в оптимальном пла­не не имеет у₃= 0.

Таким образом, положительную двойственную оценку имеют лишь те виды ресурсов, которые полностью используются в опти­мальном плане. Поэтому двойственные оценки определяют дефи­цитность ресурсов.

При подстановке оптимальных двойственных оценок в систему ограничений двойственной задачи получим:

0,1 * 23,75 + 0,05 * 12,5 +3*0 = 3;

0,2 * 23,75 + 0,02 * 12,5 +1*0 = 5;

0,4 * 23,75 + 0,02 * 12,5 + 2 * 0 > 4.

Первое и второе ограничения двойственной задачи выполня­ются как равенства. Это означает, что двойственные оценки ресур­сов, используемых для реализации единицы товаров первой и вто­рой групп, равны в точности доходам. Поэтому продавать эти виды товаров экономически целесообразно, а их реализация предусмот­рена оптимальным планом прямой задачи (x₁> 0, х₂> 0). Третье ограничение двойственной задачи выполняется как строгое нера­венство. Это означает, что двойственная оценка, используемая при реализации единицы товара третьей группы, выше дохода от его продажи. Следовательно, продавать товары третьей группы невы­годно, и в оптимальном плане прямой задачи х₃= 0.

Величина двойственной оценки показывает, насколько возрастает значение целевой функции при увеличении дефицитного ресурса на единицу. Например, увеличение рабочего времени на 1 чел.-ч приведет к получению нового оптимального плана, в котором при­быль возрастает на 23,75 и станет равной

F(X) = 27 625 + у₁ = 27 625 + 23,75 = 27648,75 тыс. руб.

При этом коэффициенты оптимальной симплексной таблицы 2 столбца х₄ показывают, что указанное увеличение прибыли достигается за счет увеличения ре­ализации второй группы товара на величину 6,25 единиц, умень­шения объема продажи первой группы товара на величину 2,5 еди­ниц и уменьшения остатка ресурса третьего вида на 62,5 м².

В то же время ввод в продажу невыгодной группы товаров умень­шает размер дохода. Если х₃ = 1, то F(X) = 27 625 - 5,75 = 27619,25 тыс. руб.

При этом коэффициенты структурных сдвигов оптимальной симплексной таблицы 2 столбца х₃ показывают, что указанное умень­шение дохода происходит за счет уменьшения объема продажи выгодного товара второй группы на величину 2,25 единиц, увели­чения продажи первой группы товара на 0,5 единиц и уменьшения остатка ресурсов третьего вида на 1,25 м².

Таким образом, двойственные оценки связаны с оптимальным планом прямой задачи. Всякое изменение исходных данных пря­мой задачи оказывает влияние на ее оптимальный план и на сис­тему двойственных оценок. В свою очередь двойственные оценки служат инструментом анализа и принятия правильных решений в условиях меняющихся коммерческих ситуаций.