§ 4. Подпоследовательности и предельные точки.

Договоримся в дальнейшем в случае б/бпоследовательности писать(+).

Определение1. Пусть даны последовательность {x_n} и возрастающая последовательность {k_n}N. Выберем из последовательности {x_n} элементы с номерамиk₁,k₂, ... Полученная таким образом последовательностьназываетсяподпоследовательностьюпоследовательности {x_n}. Будем в этом случае писать{x_n}.

Ясно, что nk_nn, причем порядок следования элементов в подпоследовательности сохраняется.

Вставка 1.

Теорема1. Пусть..

Доказательство. Пусть, т.е.> 0n₀=n₀():n >n₀|x_n – a| < ,еслиа– конечное (|x_n| > ,еслиа=). Так какk_nn, то приn>n₀будет верно(). А это и означает, что.

Следствие.Если из последовательности можно извлечь хотя бы две подпоследовательности, сходящиеся к различным пределам (конечным или бесконечным), то последовательность расходится.

Вставка 2.

Определение 2. Точканазываетсяпредельнойточкой (иличастичным пределом) последовательности {x_n}, если в любой окрестности точкиасодержится бесконечно много элементов этой последовательности.

Определение3. Точканазываетсяпредельнойточкой последовательности {x_n}, если из этой последовательности можно извлечь подпоследовательность:.

Нетрудно видеть, что в определении 2 в роли окрестности достаточно рассматривать O_(a).

Теорема2. Определения 2 и 3 эквивалентны.

Доказательство.Рассмотрим случай конечногоа(случайа=рассматривается аналогично).

1) Пусть в любой O_(a) находится бесконечно много элементов последовательности {x_n}. Рассмотрим произвольную убывающуюб/м последовательность{_n}. Ввыберем произвольный элемент, ввыберем произвольный элементтак, чтобыk₂>k₁. Это возможно, т.к. вбесконечно много элементов последовательности {x_n}. Ввыберем произвольный элементс условиемk₃>k₂и т.д.

В результате получим подпоследовательность . Так как, то по теореме о зажатой последовательности, что равносильно сходимости подпоследовательностик точкеа.

2) Пусть {x_n},. Тогда по определению предела в любойO_(a) лежат все элементы, начиная с некоторого, а их бесконечно много.

Теорема3 (Больцано – Вейерштрасса). Любая ограниченная последовательность имеет хотя бы одну конечную предельную точку.

Доказательство. Пусть последовательность {x_n} ограничена, т.е.ax_nbnN. Разделим отрезок [a,b] пополам. По крайней мере, один из полученных отрезков содержит бесконечно много элементов последовательности {x_n}. Обозначим его [a₁,b₁]. Пусть- какой-либо член последовательности {x_n} из [a₁,b₁].

Разделим отрезок [a₁,b₁] пополам. Хотя бы один из полученных отрезков содержит бесконечно много элементов последовательности {x_n}. Обозначим его [a₂,b₂] и выберем на этом отрезке элемент,k₂>k₁.

Продолжая этот процесс, получим последовательность стягивающихся сегментов {[a_n,b_n]} и подпоследовательность, для которой. По лемме Кантора, с[a,b]. Тогда по теореме о зажатой последовательности, а по определению 3 точка с является предельной для последовательности {x_n}.

Теорема3^. Если последовательность {x_n} неограниченна, тоявляется ее предельной точкой, т.е{x_n}:.

Доказательство. РассмотримО_М(), гдеМ> 0 – произвольно. Так как {x_n} неограниченна, то. ПустьМ₁>. Тогдаи т.д. продолжая этот процесс, получим, т.е.есть предельная точка последовательности {x_n}.

Теорема 4. Если точкаявляется единственной предельной точкой последовательности {x_n}, то.

Доказательство.Действительно, вне любой окрестности точкиаможет находиться только конечное число элементов последовательности {x_n}, т.к. в противном случае по теоремам 3 и 3^найдутся еще предельные точки. А это и означает, что.

Объединяя теоремы 1, 4 и определение 3, получим следующее утверждение.

Теорема 4^. Для того, чтобы, необходимо и достаточно, чтобыаявлялась единственной предельной точкой последовательности {x_n}.

Определение4. ПустьА– множество предельных точек последовательности {x_n}. ЧислоsupA(infA) называется верхним (нижним) пределом последовательности {x_n} и обозначается символом.

Следствие к теореме4^. Для того, чтобы, необходимо и достаточно, чтобы.

Вставка 3.

Вопросы иупражнения.

1. Будут ли последовательности а) 2, 5, 8, 11, … и б) 3, 2, 7, 6, 11, 10, … являться подпоследовательностями последовательности натуральных чисел {n}?

2. Какая связь между пределом и предельной точкой последовательности?

3. Построить пример последовательности с предельными точками a₁,a₂, ...,a_p.

4. Последовательности {x_n} и {y_n} имеют по одной предельной точке. Сколько предельных точек могут иметь последовательности {x_n + y_n} {x_ny_n}?

5. Доказать, что из любой ограниченной последовательности можно извлечь, сходящуюся к конечному пределу, подпоследовательность, а из любой неограниченной последовательности можно извлечь б/бподпоследовательность.

6. Любая ли подпоследовательность неограниченной последовательности является б/б?

7. Найти все предельные точки последовательности 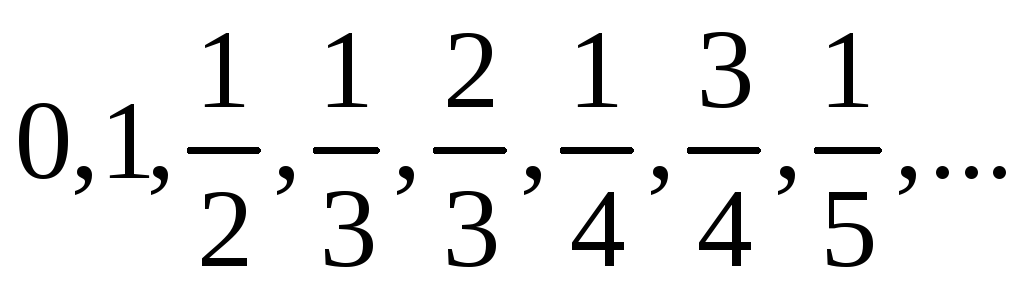. Указать.

8. Доказать, что любая ограниченная последовательность {x_n} имеет конечные.

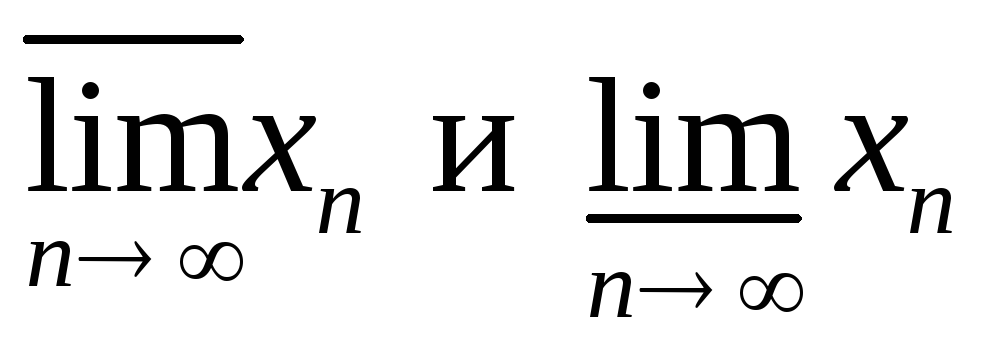9. Построить пример последовательности а)имеющей единственную конечную предельную точку, но расходящуюся;б)имеющей своими предельными точками все элементы последовательности {a_n}.

10. Доказать, что монотонная последовательность будет сходящейся, если сходится некоторая ее подпоследовательность.

21