3. Виды тел. Расчетная схема

Конструкции, с которыми приходится встречаться на практике имеют в большинстве случаев сложную форму, отдельные формы которой можно привести к следующим простым типам:

1. Брус – тело, у которого два размера малы по сравнению с третьим. В частном случае брус может иметь постоянное поперечное сечение и прямолинейную ось. В этом случае брус называют стержнем. Ось бруса – это линия, соединяющая центры тяжестей его поперечных сечений.

2. Пластинка – тело, ограниченное двумя плоскими поверхностями, расстояние между которыми мало по сравнению с прочими размерами.

3. Оболочка – тело, ограниченное двумя криволинейными поверхностями, расстояние между которыми мало по сравнению с прочими размерами.

4. Массив – тело, у которого все три размера одного порядка.

В курсе механики материалов рассматриваются преимущественно тела, имеющие форму брусьев постоянного сечения и простейшие системы, состоящие из них.

Расчет реальных конструкций на действие реальных внешних нагрузок производится с помощью так называемых расчетных схем. При составлении расчетных схем нагрузку, приложенную к небольшим участкам поверхности бруса, заменяют сосредоточенной силой и переносят к оси бруса. Точки приложения сил на оси бруса и сосредоточенных моментов, возникающих из-за переноса сил. располагают в тех же поперечных сечениях. На расчетной схеме вместо бруса изображается его ось.

На рис. 1 вверху приведены реальный брус и под ним расчетная схема. При переносе сил F₂ и F₃ на ось, согласно правилам теоретической механики. нужно добавить моменты сил: и, гдеa₂ и a₃ - плечи сил F₂ и F₃. Сила F, переносится по линии действия, поэтому момент силы не возникает.

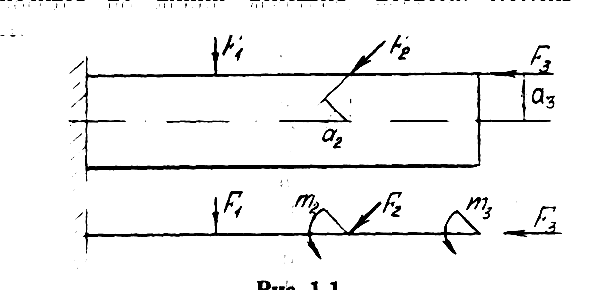
Рис. 1

При составлении расчетных схем необходимо иметь в виду, что правила теоретической механики в сопротивлении материалов иногда применять нельзя. Например, если требуется определить напряжения и деформации стержня, нельзя переносить силу по линии действия (см. рис. 2). Если силу перенести из точки 1 в точку 2, то стержень окажется ненагруженным.

Рис. 2

Нельзя слагать силы, если они не действуют в одной точке (см. рис. 3)

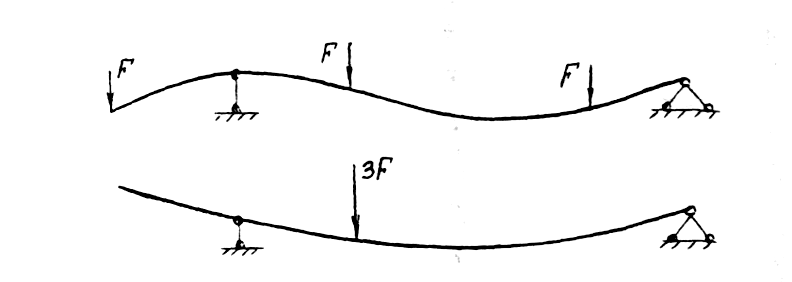
Рис. 3

Пусть на одинаковом расстоянии одна от другой действуют три силы F. Если силы сложить, то будет одна сила, равная 3F, и действующая по направлению средней. Прогиб балки тогда изменится (сравните верхний и нижний рисунок).

4. Допущения, принимаемые в механике материалов

Расчет конструкций и их элементов с учетом всего многообразия физико-механических свойств реальных материалов является или теоретически невозможным, или практически неприемлемым по своей сложности. Поэтому, отказываясь от принятой в теоретической механике модели абсолютно твердого тела, в механике материалов приходится вводить свою модель – модель идеализированного деформируемого тела. Поэтому необходимо сделать ряд допущений.

1–е допущение. Материал тела имеет сплошное (непрерывное) строение, т.е. не имеет пустот.

2–е допущение. Материал конструкции является однородным, т.е. его свойства одинаковы во всех точках.

Заведомо неоднороден такой материал, как бетон. Он состоит из бессистемно разбросанных зерен заполнителя (гравия, щебня, песка и пр.) различной крупности и формы, которые скреплены цементной массой. Но размеры бетонных элементов велики по сравнению с размерами зерен, поэтому бетон считают однородным.

3–е допущение. Материал конструкции изотропен, т.е. его свойства по всем направлениям одинаковы.

Эта предпосылка используется при решении большинства задач. Для некоторых материалов, например, дерева свойства вдоль и поперек волокон существенно различаются. Такие материалы называют анизотропными. При решении ряда задач необходимо учитывать анизотропность материала.

4–е допущение. В теле до приложения нагрузки нет внутренних усилий. Внутренние усилия, вызванные неравномерностью остывания (металл) или высыхания (дерево) или затвердения (бетон), не учитываются.

5–е допущение или принцип независимости действия сил.

“Результат воздействия на тело системы сил равен сумме результатов воздействия тех же сил, приложенных к нему последовательно и в любом порядке”.

Под словами “результат воздействия” следует понимать деформации, внутренние силы, возникающие в теле и перемещения отдельных точек конструкции.

Например, на балку (см. рис. 4) действуют две силы F₁ и F₂. Прогиб в точке К можно определить, как прогиб отдельно от силы F₁ и от силы F₂ и сложить.

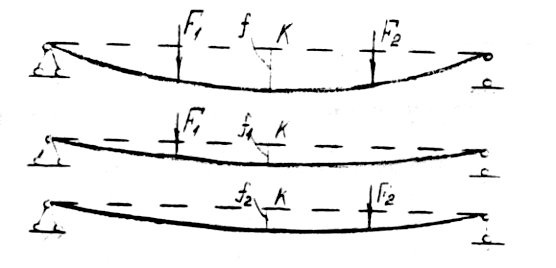
Рис. 4

f = f_l+f₂,

где f₁ и f₂ – прогибы от каждой силы в отдельности.

Принцип независимости действия сил применим при следующих двух условиях:

а) перемещение точек приложения сил малы по сравнению с размерами тела;

б) перемещения, являющиеся результатом деформации тела, линейно зависят от действующих сил, т.е. подчиняются закону Гука.