Пример №2

Необходимо определить диаметр круглого стального бруса переменного сечения, заделанного с двух сторон (рисунок 7, а) из условия прочности, когда и жесткости, когда, если. Модуль сдвига стали

Решение

Так как в одно уравнение равновесия () войдут два неизвестных – реактивные моменты в заделках, то задача является один раз статически неопределимой.

Для составления уравнения деформаций изобразим эквивалентную систему (рисунок 7, б), отбросив правую заделку и заменив ее моментом х. Уравнение деформаций выражает условие отсутствия угла поворота сечения 1. Из этого следует, что угол закручивания всего бруса равен нулю.

Формула для угла закручивания –

Уравнение деформаций принимает вид:

Выразим (полярный момент инерции сечения на участке 3-4) через момент инерцииучастка 1-3.

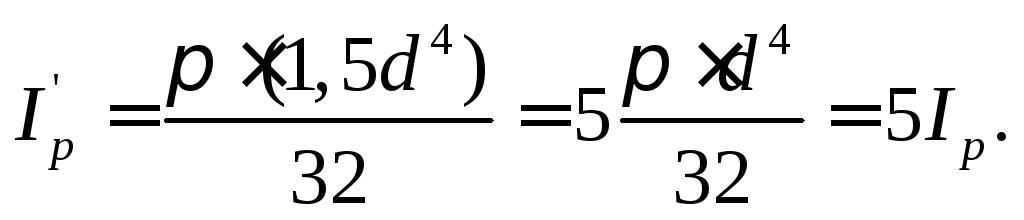
Выполним эту подстановку и решим уравнение получим

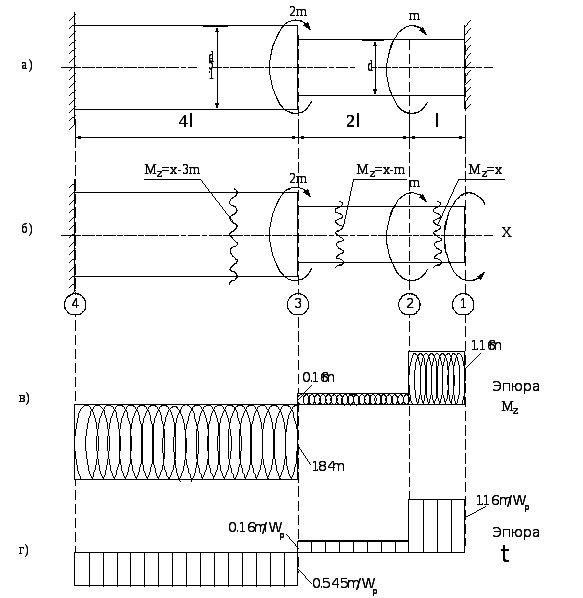
Рисунок 7 − К расчету стального бруса при кручении

Строим эпюру крутящего момента М_z (рисунок 7, в). Обратим внимание, что скачки на эпюре будут в тех сечениях, в которых приложены внешние моменты (на величину этих моментов).

Далее строим эпюру касательных напряжений, действующих в точках контура поперечных сечений (рисунок 7, г).

Участок 1-2: Участок 2-3:

Для определения касательных напряжений на участке 3-4 выразим момент сопротивления через:

Наибольшие касательные напряжения оказались на участке 1-2. Записываем условие прочности:

Найдем диаметр из условия жесткости. Относительный угол закручивания на участке 1-2:

На участке 3-4:

Условие жесткости:

Принимаем окончательно из условия прочности d=60 мм.

Пример № 3

Для сечения (рисунок 8) необходимо найти положение главных центральных осей и вычислить главные моменты и главные радиусы инерции.

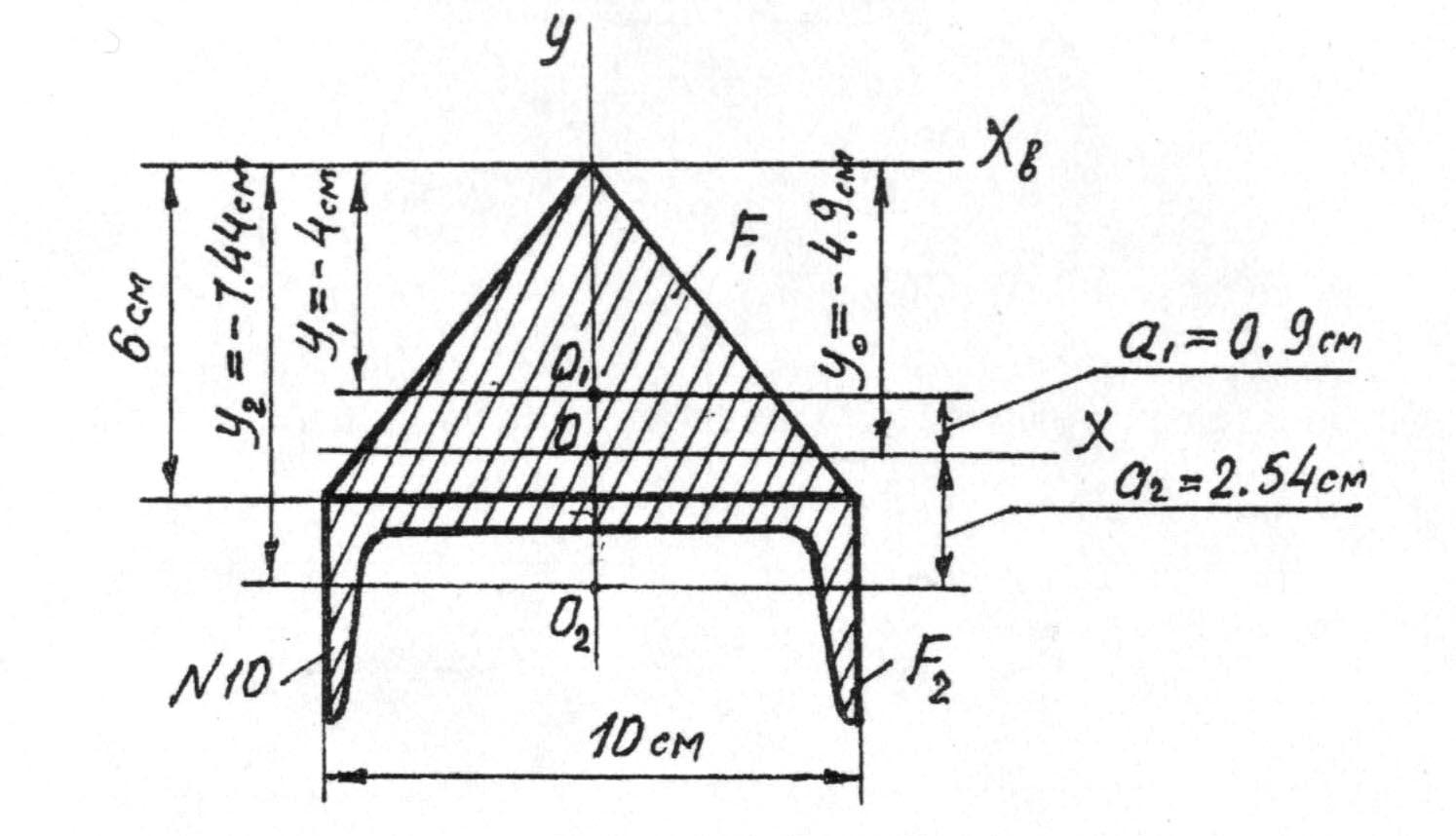
Рисунок 8 − Схема составного сечения

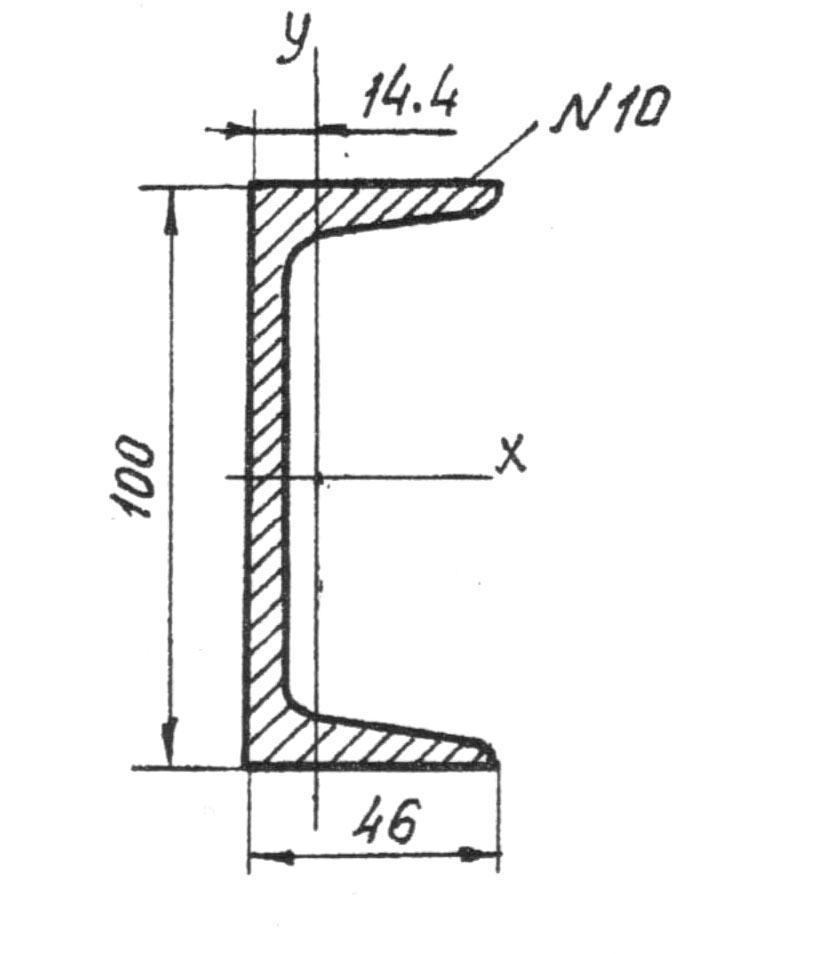
Из сортамента прокатных профилей выписываем данные по швеллеру №10У (ГОСТ 8240-97), изображенному на рисунке 9.

А = 10,90 см2; Ix = 174,0 см4; Iу = 20,40 см4.

Рисунок 9. Схема сечения швеллера

Решение

Через вершину треугольника проводим вспомогательную ось Х_в и определяем координату Y₀ центра тяжести сечения.

Проводим центральную ось Х и находим расстояние а₁ и а₂ между осью Х и параллельными ей центральными осями треугольника и швеллера.

Вычисляем главные моменты инерции сечения.

Для треугольника использованы следующие формулы (рисунок 10).

Рисунок 10 − К расчету главных моментов инерции

Вычисляем главные радиусы инерции сечения:

Пример № 4

Для заданной балки (рисунок 11) необходимо:

1. Построить эпюры поперечных сил и изгибающих моментов.

2. Из расчета на прочность подобрать двутавровое, круглое и прямоугольное сечение (приняв для прямоугольного сечения отношение высоты к ширине, равное двум), если .

Решение

Реакции опор R_в и R_д направим вверх. Составим уравнение статического равновесия.

 = 0;

Fl – q1,5(1,5/2) – m + R_Д2,5 = 0; R_Д = 11,5кН.

= 0;

F3,5 – R_В2,5 + q1,5(1,5/2 + 1 ) – m = 0; R_В = 73,5 кH.

Проверка:

= 0; – F + R_В – q1,5 + R_Д = 0;

–40 + 73,5 – 401,5 + 11,5 = 0;

–85 + 85 = 0.

Реакции опор определены верно.

Определим значение поперечной силы Q в сечении на участке АВ, рассматривая левую часть балки. Поперечная сила в сечении численно равна алгебраической сумме всех внешних сил, действующих на рассматриваемую часть балки.

Q₁ = –F = –40 кН.

Знак «минус» берется потому, что сила слева направлена вниз (см. правило знаков для Q). Поскольку Q – величина постоянная, на эпюре Q изображается в виде горизонтальной прямой.

Дальнейшее решение будем выполнять справа. Следует учесть, что знаки для Q будут обратными (см. правила знаков). Для сечения между D и С:

Q₂ = –R_Д = –11,5 кH.

Эпюра на этом участке также изображается горизонтальной прямой. Определим Q между С и В:

Q₃ = –R_Д + q(z₃–1) = –11,5 + 30(z₃–1).

Это уравнение наклонной прямой. Чтобы ее построить, определим две точки на концах участка:

z₃ = 1 м, Q₃ = –11,5 кН;

z₃ = 2,5 м, Q₃ = –11,5 + 30(2,5–l) = 33,5 кН.

Откладываем наклонную прямую по этим точкам. Она пересекает нулевую линию. В точке пересечения Q = 0, и, следовательно, эпюра моментов имеет экстремум, поэтому значение z для этой точки нужно определить.

Q₃ = –11,5 + 30(z₃–1) = 0;

или

z₃ = 41,5/30 = 1,38 м.

Проверим эпюру Q на правильность построения. Значения Q для правой и левой части должны совпасть, если в сечении не приложена сосредоточенная сила. Если же сила приложена, то значение Q должно различаться на величину этой силы. В точке В приложена сила R_В = 73,5 кН и Q различается на эту величину.

Определим изгибающий момент на первом участке. Изгибающий момент в сечении равен алгебраической сумме всех внешних моментов, вычисленных относительно сечения и приложенных к рассматриваемой части балки:

M₁ = –Fz₁ = –40 z.

Это уравнение наклонной прямой.

при z₁ = 0, M₁ = 0;

z₁ = l м, М₁ = –40 кНм.

На втором участке:

M₂ = R_Дz₂ = 11,5 z₂;

при z₂ = 0, M₂ = 0;

z₂ = 1 м, М₂ = 11,5 кНм.

На третьем участке:

M₃ = R_Дz₃ – q(z₃ – 1)(z₃ – 1)/2 – m = 11,5z₃ – 15(z₃ – 1)² – 35.

Это уравнение параболы, так как z во второй степени. Для построения параболы необходимо определить 3 точки: по краям участка и экстремальное значение. Парабола строится дугой навстречу распределенной нагрузке. При:

z₃ = 1 м, М₃ = 11,5 – 35 = –23,5 кНм,

z₃ = 1,38 м, М₃ = 11,5 – 1,38 – 15(1,38 – 1)² – 35 = –21,3 кНм,

z₃ = 2,5 м, M₃ = 11,5 – 2,5 – 15(2,5 – l)² – 35 = –40 кHм.

Проверим правильность построения эпюры М. Значения изгибающих моментов для левой и правой части должны совпасть, если в сечении нет внешнего момента, и различаться на величину внешнего момента, если он приложен. В сечении В нет внешнего момента, а изгибающий момент слева и справа одинаков. Следовательно, эпюра М построена правильно.

Опасным является сечение, в котором изгибающий момент максимальный без учета знака. Опасным будет сечение В, для которого

Сечение балки подбирают по формуле:

.

По таблице сортамента, приведенной в приложении (таблица 6), находим двутавр № 20а W_х = 203 см³.

Для круглого сечения:

.

Для прямоугольного сечения:

.

По условию задачи h = 2b, поэтому,

откуда ;

Сравнение 1 м веса балки можно произвести по площади поперечного сечения разных профилей:

− для двутавра (см. таблицу 6 приложения);

− для круга

− для прямоугольника

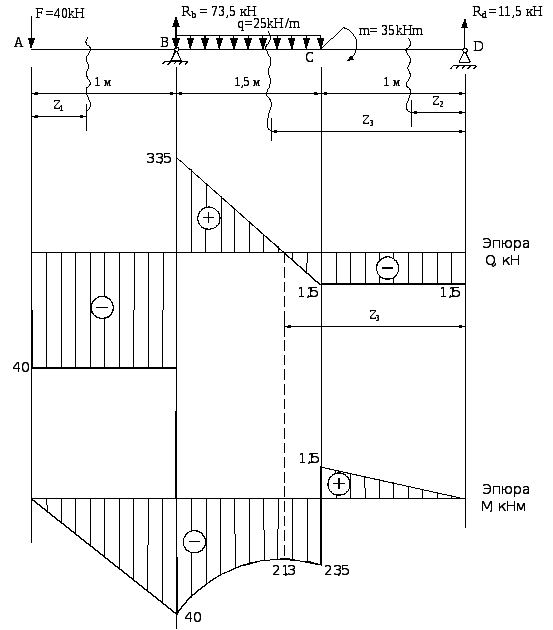
Рисунок 11 − Схема балки и эпюры внутренних усилий

Если двутавровое сечение принять за единицу, то соотношение профилей будет:

− для круглого сечения 124,5/32,8 = 3,8;

− для прямоугольного 91,2/32,8 = 2,78.

Следовательно, при использовании балки круглого сечения расход материала увеличивается в 3,8 раз, прямоугольного – в 2,78 раза.