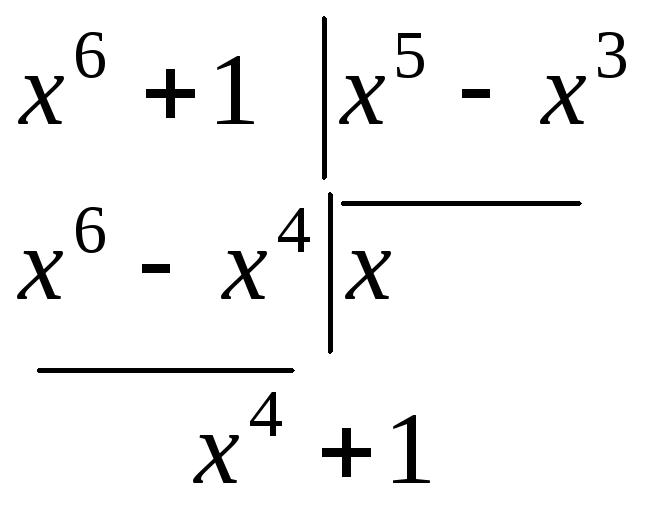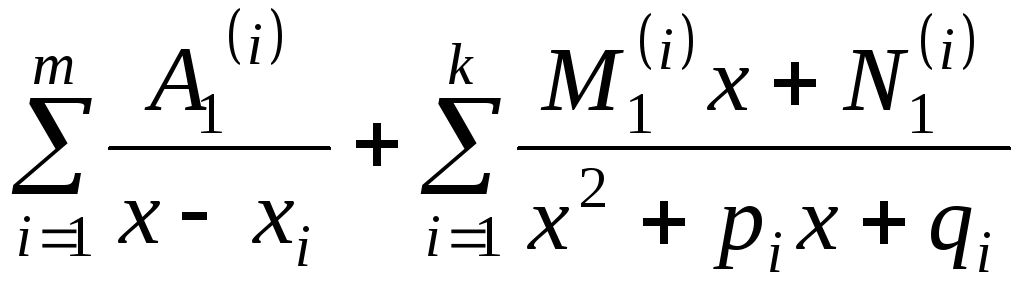Lektsii_Rubleva_1 / Гл 03 _нтеграл Ньютона-Лейбн_ца / Пар 3-03 _нтегрування рац_ональних функц_й

4

Глава 3

Інтеграл Ньютона-Лебніца

3. Інтегрування раціональних функцій

1-й крок.	Виділення цілої частини.
	, де - многочлен.

2-й крок.

Інтегрування правильного дробу.

Метод 1. Метод невизначених коефіцієнтів.

Теорема 1.	(Розклад множини на множники).
	Будь-який многочлен можна подати у вигляді:
		(1)
	де корені многочлена , а квадратні двочлени не мають дійсних коренів.

Теорема 2.	(Розклад правильного дробу).
	Якщо дріб правильний і має вигляд (1), то його можна надати у вигляді:
		(2)

Таким чином інтегрування правильного дробу зводиться до інтегрування чотирьох типів правильних дробів:

1) ;	;
2) ;	;
3) ;	;
4) , .	.

Приклад 1.
.
Похідна і підставимо

Метод 2. Метод Остроградського.

Розглянемо праву частину формули (2). Які з доданків при інтегруванні дають нераціональні доданки? Випишемо їх:

(3)

При інтегруванні решти доданків, ми одержимо раціональні вирази із ступінню знаменника на 1 менше, ніж у підінтегрального вирізу. Якщо їх об’єднати, то можемо записати таку формулу (якщо дріб - правильний, і має розгляд (1)) .

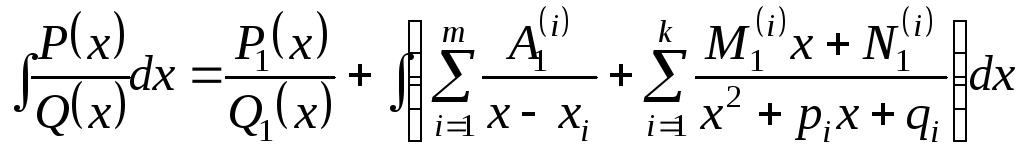Тут , а - многочлен з невідомими коефіцієнтами, ступінь якого на 1 менше за ступінь (бо дріб правильний). Ці коефіцієнти знаходяться шляхом диференціювання останньої тотожності:

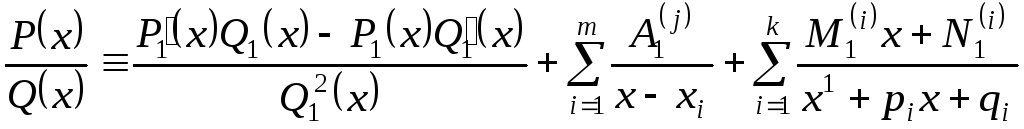, легко зрозуміти, що спільний знаменник буде саме , тому що буде доведено нижче.

Приклад 2.	.

; ; ;

.

; .

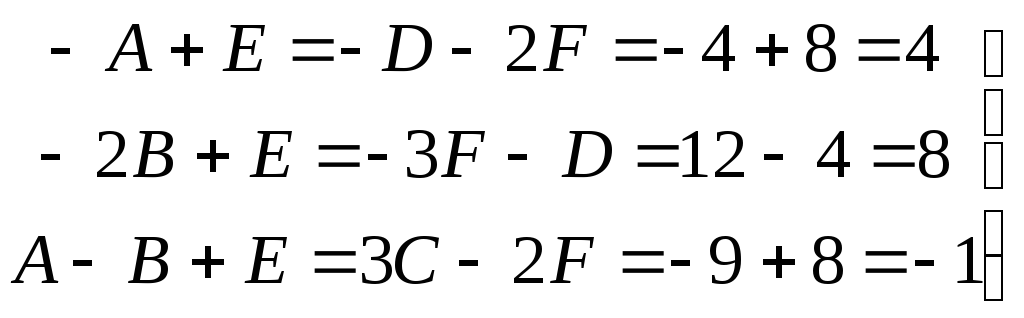
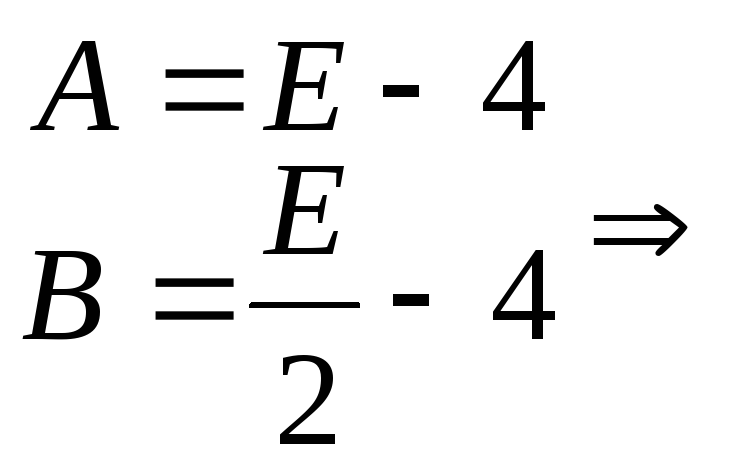
Цей варіант методу Остроградського слушно застосовувати, якщо в явному вигляді виділені корені знаменнику. Розглянемо трохи інший випадок. Корені знаменника або не виділені, або навіть взагалі їх виділити неможливо.

Позначимо для правильного дробу через НСД многочленів , нехай тоді . Позначимо через многочлени з невизначеними коефіцієнтами, кожний з яких має степінь на одиницю менший за степінь від степені відповідного з многочленів . Запишемо тотожність для знаходження коефіцієнтів многочленів :

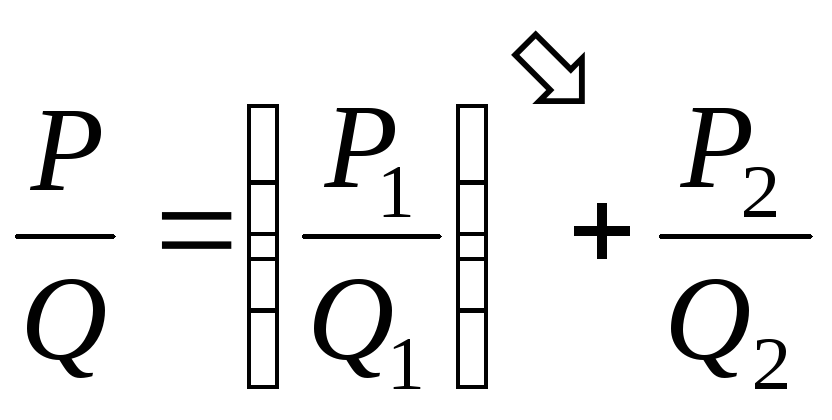, (4)

її права частина може бути записаною у вигляді:

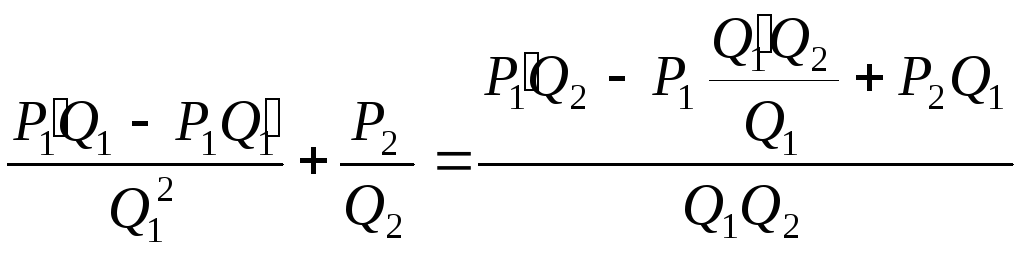. Доведемо, що спільним знаменником є саме многочлен , тобто дріб є многочленом. Для доведення цього запишемо тотожність: , тому що є дільником многочлена . Після цього, прирівнюючи коефіцієнти многочленів і , дістанемо систему рівнянь для відшукання коефіцієнтів многочленів .

Тотожність (4) зводить знаходження первісної функції до аналогічної, але більш простої задачі для функції .

Приклад 3.

.

, .

За алгоритмом Евкліда знайдемо НСД .

;

; НСД буде многочлен: . Знайдемо діленням многочлен:

, тому формула (4) набуває вигляду:

, для вказаних многочленів запишемо тотожність: .

.

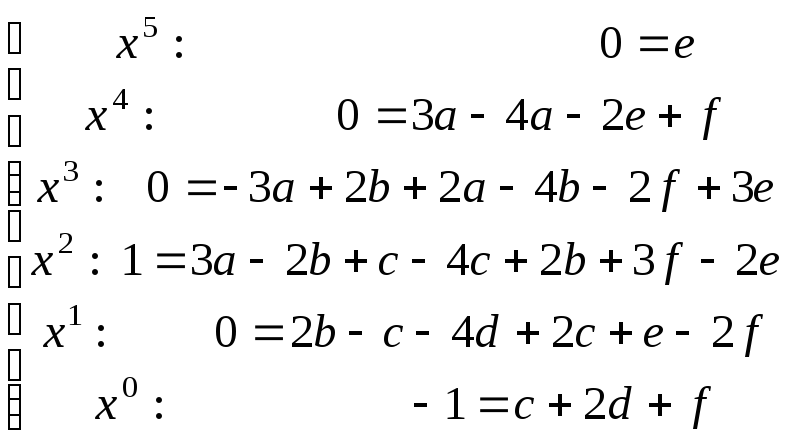
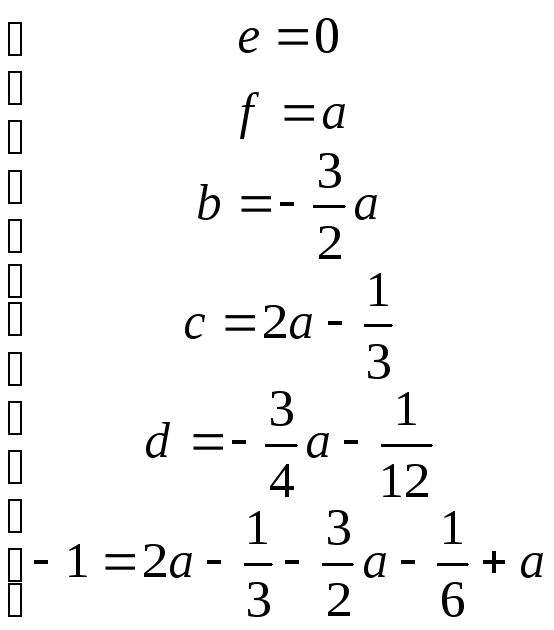
Подальше інтегрування не викликає великих проблем.
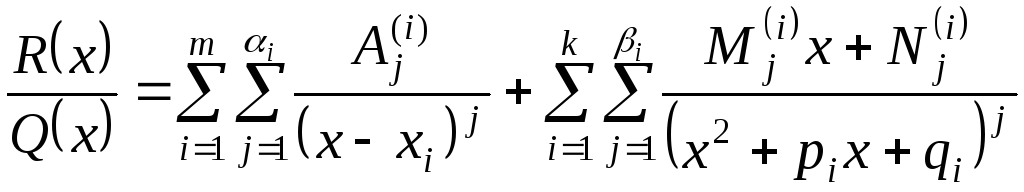
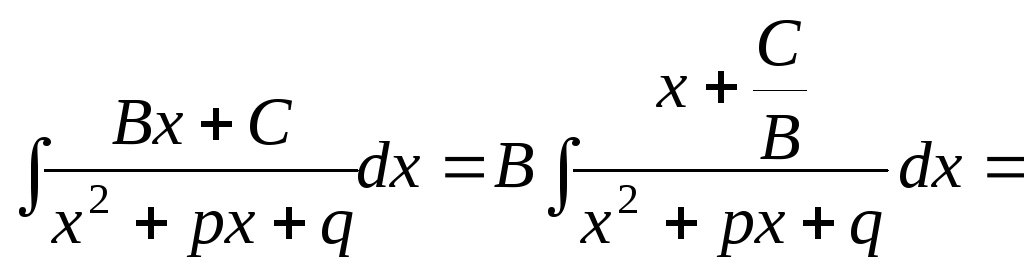
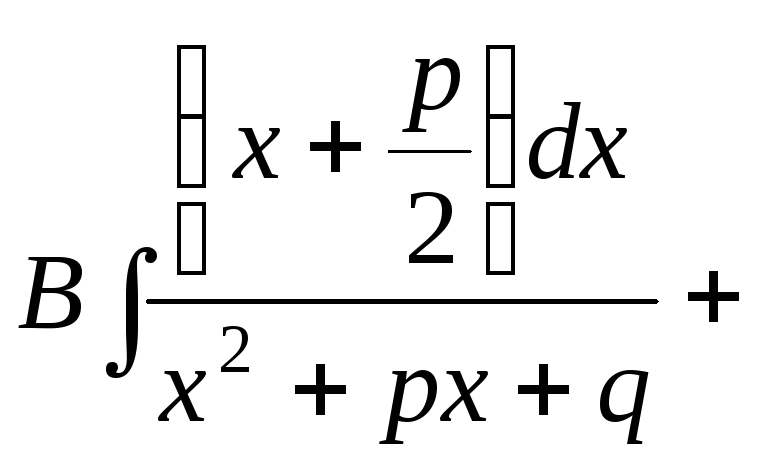
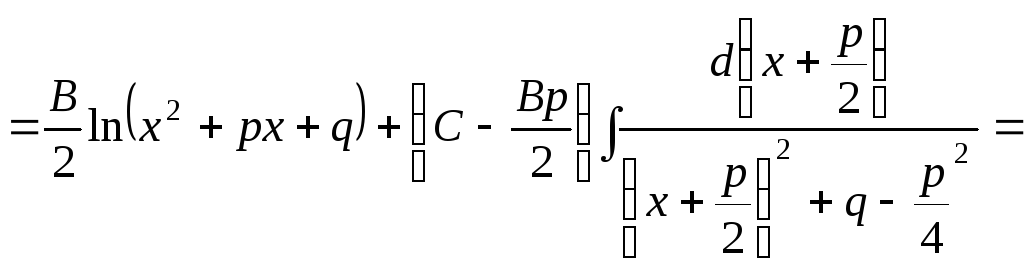