
Lektsii_Rubleva_1 / Гл 10 М_ра Лебега / Задач_ 10-3 М_ра Вим_рн_ множини
.doc
Глава 10
Міра Лебега
3. Міра. Зовнішня міра. Вимірні множини
Теорія
Нехай
в деякому просторі
![]() визначена алгебра множин A,
на якій задана дійсна функція множин
визначена алгебра множин A,
на якій задана дійсна функція множин
![]() A
A![]() .
Ця функція називається мірою,
якщо виконуються умови:
.
Ця функція називається мірою,
якщо виконуються умови:
1)
![]() ;
;
2)
![]() для будь-якої диз’юнктної послідовності
множин
для будь-якої диз’юнктної послідовності
множин
![]() (злічена
адитивність,
або
(злічена
адитивність,
або
![]() -адитивність).
-адитивність).
При
цьому міра називається скінченою,
якщо
![]() .
.
Міра
називається
![]() скінченою,
якщо існує монотонно зростаюча
послідовність множин
скінченою,
якщо існує монотонно зростаюча
послідовність множин
![]() A:
A:
![]() і
і
![]() .
.
|
Властивості |
Міри: |
|
1. |
(Монотонність) |
|
|
Якщо
|
|
2. |
(Субтрактивність) |
|
|
Якщо
|
|
3. |
(Злічена напівадитивність) |
|
|
|
Нехай
на деякій алгебрі множин A
визначена міра
![]() .
Тоді
.
Тоді
![]() визначимо функцію
визначимо функцію
![]() , (1)
, (1)
де
інфінум береться по всіх таких
послідовностях множин
![]() A,
що покривають задану множину
A,
що покривають задану множину
![]() (очевидно, що такі послідовності існують,
в якості однієї можливої можемо покласти
(очевидно, що такі послідовності існують,
в якості однієї можливої можемо покласти
![]() ,
,![]() ).
Функцію
).
Функцію
![]() ,
що визначена на
,
що визначена на
![]() назвемо зовнішньою
мірою.
назвемо зовнішньою
мірою.
|
Властивості |
Зовнішньої міри: |
|
1. |
(зовнішня міра на алгебрі) |
|
|
Якщо
|
|
2. |
(невід’ємність зовнішньої міри) |
|
|
|
|
3. |
(монотонність зовнішньої міри) |
|
|
|
|
4. |
(напівадитивність зовнішньої міри) |
|
|
|
|
Зауваження. |
Інколи
буває зручним визначати зовнішню міру
аксіоматично. Дійсна функція
|
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
Якщо
на алгебрі множин
![]() визначено за формулою (1)
зовнішню міру, при цьому
визначено за формулою (1)
зовнішню міру, при цьому
![]() (міра усього простору скінчена), то можна
визначити внутрішню
міру
(міра усього простору скінчена), то можна
визначити внутрішню
міру
![]() ,
за формулою:
,
за формулою:
![]()
![]() .
.
Більшість
з наведених далі тверджень справджуються
для будь-яких мір, для доведення інших
треба звузити клас мір
![]() скінченними.
скінченними.
Множина
![]() називається вимірною
(вимірною
за Каратеодорі),
якщо
називається вимірною
(вимірною
за Каратеодорі),
якщо
![]() виконується рівність:
виконується рівність:
![]() .
.
Сукупність
усіх вимірних множин позначимо
A,
а звуження зовнішньої міри
![]() на A
позначимо
на A
позначимо
![]() .
.
|
Теорема 1. |
(Сукупність вимірних множин) |
|
|
Сукупність
A
вимірних множин утворює
|
|
Теорема 2. |
(Існування продовження міри) |
|
|
Нехай
A
- деяка алгебра,
|
Нехай
A
- деяка алгебра,
![]() - міра на A.
Позначимо A
- міра на A.
Позначимо A![]() породжену цією алгеброю
породжену цією алгеброю
![]() алгебру
(мінімальну), побудуємо продовження
алгебру
(мінімальну), побудуємо продовження
![]() міри
міри
![]() на A
на A![]() .
Таке продовження називають мінімальним
продовженням.
.
Таке продовження називають мінімальним
продовженням.
|
Зауваження. |
Якщо
|
Міра
![]() ,
що задана на алгебрі A,
називається повною,
якщо з умов
,
що задана на алгебрі A,
називається повною,
якщо з умов
![]() A,
A,
![]() та
та
![]() ,
слідує, що
,
слідує, що
![]() A.
Зрозуміло, з монотонності міри, що при
цьому
A.
Зрозуміло, з монотонності міри, що при
цьому
![]() .
.
|
Теорема 3. |
(Про множини нульової міри) |
|
|
Нехай
|
|
Наслідок. |
(Повнота
|
|
|
Міра
|
|
Теорема 4. |
(Неперервність знизу) |
|
|
Нехай
|
|
Теорема 5. |
(Неперервність зверху) |
|
|
Нехай
|
|
Теорема 6. |
(Критерій вимірності) |
|
|
Нехай
|
Система
M
підмножин простору
![]() називається монотонним
класом,
якщо разом з будь-якою монотонною
послідовністю множин
називається монотонним
класом,
якщо разом з будь-якою монотонною
послідовністю множин
![]() вона містить також її границю
вона містить також її границю
![]() .
.
|
Лема 1. |
(Кільце - монотонний клас) |
|
|
|
Якщо
кільце множин R
є монотонним класом, то R
-
|
|
|
Теорема 7. |
(Про мінімальний монотонний клас) |
|
|
|
Нехай
R
- деяке кільце. Позначимо через R |
|
|
Теорема 8. |
(Про єдиність мінімального продовження міри) |
|
|
|
Нехай
A
- деяка алгебра, A |
|
Задачі
-
Довести твердження:
а)
нехай
![]() - міра на алгебрі множин A,
тоді
- міра на алгебрі множин A,
тоді
![]() A,
A,
![]() A
мають місце співвідношення:
A
мають місце співвідношення:
1)
![]() ;
;
2)
![]() ;
;
3)

4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]()
![]() ;
;
8)
![]() ;
;
9)
для будь-якої скінченої або зліченої
сукупності множин
![]() A
A
![]() ;
;
10)
якщо
![]() ,
то
,
то
![]() ;
;
б)
адитивна функція
![]() A
A![]() є мірою на алгебрі A
тоді і тільки тоді, коли
є мірою на алгебрі A
тоді і тільки тоді, коли
![]() -
-
![]() адитивна;
адитивна;
в)
нехай
![]() - зовнішня міра на
- зовнішня міра на
![]() алгебрі
множин
алгебрі
множин
![]() ,
тоді
,
тоді
![]() мають місце умови:
мають місце умови:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
якщо принаймні одна з множин
![]() чи
чи
![]() вимірна, то в попередньому пункті має
місце рівність;
вимірна, то в попередньому пункті має
місце рівність;
5)
якщо до довільної множини
![]() додати чи відняти множину
додати чи відняти множину
![]() міри нуль, то для одержаної множини
міри нуль, то для одержаної множини
![]()
![]() ;
;
6) зовнішня міра може бути не адитивною;
г)
внутрішня міра
![]() в просторі зі скінченою мірою має
властивості:
в просторі зі скінченою мірою має
властивості:
1)
невід’ємність
![]() ;
;
2) монотонність;
3)
![]() ;
;
4) злічена-напівадитивність;
5)
![]() ;
;
6)
множина
![]() - вимірна
- вимірна
![]()
![]() ;
;
д)
нехай міра
![]() визначена на
визначена на
![]() -
алгебрі A,
-
алгебрі A,
![]() A,
тоді:
A,
тоді:
1)
![]() ;
;
2)
![]() ,
якщо
,
якщо
![]() ;
;
3)
множина R![]() A
A![]() є кільцем;
є кільцем;
4)
R![]() A
A![]() ,
,![]()
![]() A,
A,![]() є
є
![]() кільцем;
кільцем;
5)
якщо для деякої множини
![]() і
і
![]()
![]() A:
A:
![]() та
та
![]() ,
то
,
то
![]() - вимірна;
- вимірна;
е)
в просторі
![]() монотонними класами є:
монотонними класами є:
1)
![]() ;
;
2)
будь-яке
![]() кільце
R
в
кільце
R
в
![]() ;
;
є) перетин будь-якої кількості монотонних класів є монотонним класом;
ж)
нехай M
- деяка
система підмножин основного простору,
M![]() ,
M
,
M![]() - відповідно найменша
- відповідно найменша
![]() алгебра
та найменший монотонний клас, що містить
множину M,
тоді M
алгебра
та найменший монотонний клас, що містить
множину M,
тоді M![]()
![]() M
M![]() ;
;
з)
якщо
![]() деяка функція, функція множин
деяка функція, функція множин
![]() ,
що визначена на півкільці
,
що визначена на півкільці
![]() півінтервалів дійсної осі, задається
таким чином:
півінтервалів дійсної осі, задається
таким чином:
![]() ,
тоді
,
тоді
![]() - міра на
- міра на
![]()
![]()
![]() - неспадна та неперервна зліва на
- неспадна та неперервна зліва на
![]() функція;
функція;
-
Нехай
 - міра на алгебрі множин A,
знаючи міри множин
- міра на алгебрі множин A,
знаючи міри множин
 (
( A),
знайти міри множин:
A),
знайти міри множин:
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
-
Перевірити твердження:
а)
якщо
![]() міри на алгебрі A,
то функція
міри на алгебрі A,
то функція
![]() ,
,
![]() є мірою на A;
є мірою на A;
б)
функція
![]() є мірою на алгебрі множин A
є мірою на алгебрі множин A![]() ,
де:
,
де:
1)
![]() ;
;
2)
![]() ,
де
,
де
![]() - фіксована точка простору
- фіксована точка простору
![]() ;
;
3)
![]() ,
де
,
де
![]() - фіксовані точки простору
- фіксовані точки простору
![]() ;
;
4)
![]() ,
де
,
де
![]() - фіксована послідовність точок простору
- фіксована послідовність точок простору
![]() ;
;
5)
 ,
де
,
де
![]() - фіксована послідовність точок простору
- фіксована послідовність точок простору
![]() ;
;
в)
для вказаного простору
![]() на
на
![]() алгебрі
алгебрі
![]() задана міра буде
задана міра буде
![]() скінченою,
де:
скінченою,
де:
1)
![]() ,
,
![]() ;
;
2)
![]() ,
,
 ;
;
3)
![]() ,
,
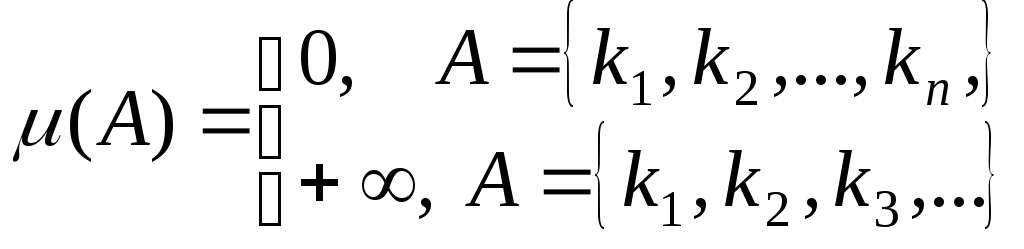 ;
;
4)
![]() ,
задана функція
,
задана функція
![]() і
і
 ;
;
г) зовнішня міра напівадитивна;
д)
якщо
![]() зовнішні міри на
зовнішні міри на
![]() ,
то зовнішньою мірою також є функція:
,
то зовнішньою мірою також є функція:
1)
![]() ;
;
2)
![]() ,
,
![]() ;
;
е)
функція
![]() є зовнішньою мірою у розумінні
аксіоматичного означення на алгебрі
множин A
є зовнішньою мірою у розумінні
аксіоматичного означення на алгебрі
множин A![]() ,
де:
,
де:
1)
![]() ,
де
,
де
![]() - фіксована точка простору
- фіксована точка простору
![]() ;
;

 .
.