Lektsii_Rubleva_1 / Гл 10 М_ра Лебега / Задач_ 10-1 Теор_я множин

4

Глава 10

Міра Лебега

1. Теорія множин

Теорія

Нехай - основний простір, всі елементи, а також множини, що розглядаються в даному розділі належать цьому простору.

Нехай деяка послідовність множин з . Назвемо верхньою границею послідовності множин множину усіх , що належать нескінченній кількості множин з , і позначимо її через ; нижньою границею послідовності множин множину усіх , що належать всім множинам з , починаючи з деякої, і позначимо її через . Будемо казати, що послідовність множин має границю, якщо виконується рівність , множину, що є спільним значенням цих двох границь будемо називати границею послідовності позначатимемо .

Непорожня система множин R називається кільцем, якщо вона замкнена відносно операцій об’єднання та різниці, тобто з умови R , R слідує, що R, R .

Алгеброю A множин називається кільце R підмножин множини , що містить .

Диз’юнктним об’єднанням сукупності множин називається об’єднання попарно неперетинаючихся множин, таку систему множин також називатимемо диз’юнктною.

Лема 1.	(Подання об’єднання через диз’юнктне об’єднання)
	Нехай - довільна послідовність множин, що належить кільцю R . Тоді існує така диз’юнктна послідовність множин R , що задовольняє умови: 1) ; 2) , .

Кільце множин R (алгебра множин A) називається кільцем (сигма кільцем) (алгеброю), якщо воно разом з довільною послідовністю містить також і їх об’єднання . (Замкненість відносно зліченого об’єднання, або об’єднання).

Для будь-якої не порожньої системи множин підмножин множини назвемо R кільцем, що породжується множиною (породженим кільцем), або кільцевою оболонкою множини , таке кільце, що містить , а також само міститься в будь-якому іншому кільці, що містить . Повністю аналогічно визначається породжена алгебра, кільце, алгебра.

Теорема 1.	(Про породжене кільце)
	Для будь-якої не порожньої системи підмножин множини існує одне і тільки одне породжене кільце R.

Півкільцем назвемо сукупність множин, що є замкненим відносно перетину, а також має властивість: : .

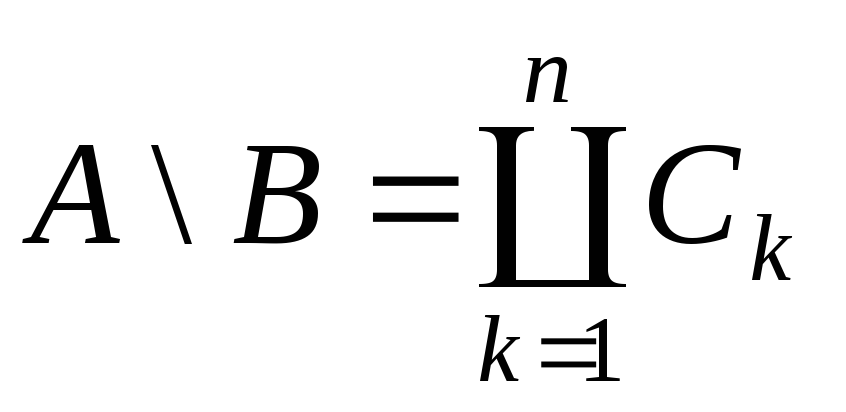Задачі

1. Довести твердження:

а) ;

б) ;

в) ;

г) ;

д) , якщо послідовність множин монотонно зростаюча, тобто ;

е) , якщо послідовність множин монотонно спадна, тобто ;

ж) якщо - послідовність множин, а - послідовність їх характеристичних функцій, то характеристичною функцією множини буде функція , а характеристичною функцією множини буде функція ;

з) ;

и) .

2. Довести, що

а) кільце замкнене відносно операцій:

1) перетину ;

2) симетричної різниці ;

3) скінченого перетину ;

4) скінченого об’єднання ;

б) кільце замкнено відносно операції зліченого перетину ;

в) система множин R є кільцем, якщо вона замкнена відносно операцій:

1) ; 2) ; 3) ;

г) якщо алгебра A замкнена відносно зліченого перетину, то A - алгебра;

д) R - деяка сукупність множин, R̃̃ - множина їх характеристичних функцій, тоді R є кільцем тоді і тільки тоді, коли R̃ є алгебраїчне кільце відносно додавання та множення за модулем ;

3. З’ясувати, чи буде наведена система множин B півкільцем, кільцем, алгеброю, 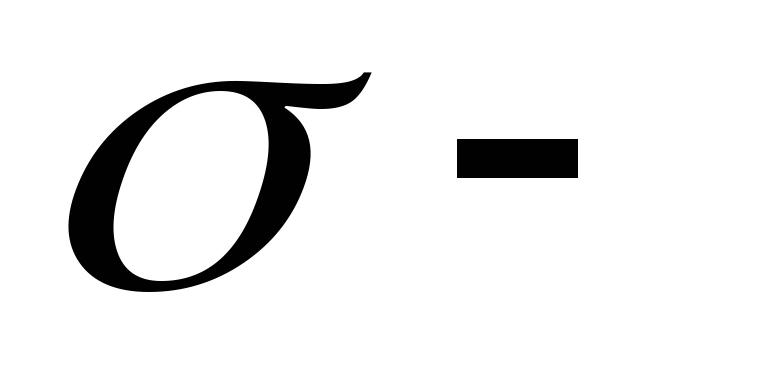кільцем чи алгеброю в просторі 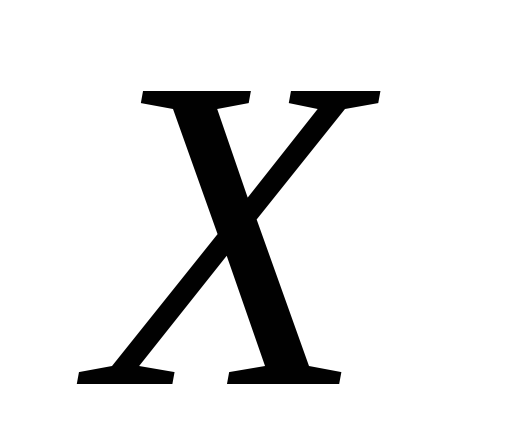, де:

а) - довільна множина, B;

б) , B - сукупність скінчених підмножин ;

в) , B - сукупність обмежених підмножин ;

г) - довільна множина, B;

д) , B - сукупність множин, що складається із об’єднань скінченої кількості півінтервалів ;

е) , B;

є) , B ;

ж) , B;

з) _, B _де:

_{1) множиною задається будь-який з чотирьох типів проміжків інтервал , півінтервал чи , або сегмент ;}

_{2) множиною задається інтервал ;}

_{3) множиною задається півінтервал ;}

_{4) множиною задається півінтервал ;}

_{5) множиною задається сегмент ;}

4. Довести твердження:

а) кільце R, що породжене множиною - це сукупність множин, що утворюються з множин в результаті застосування скінченої кількості операцій об’єднання та віднімання.

б) довести, що для довільної множини підмножин множини існує і єдина породжена:

1) алгебра;

2) кільце;

3) алгебра.

5. Перевірити твердження:

а) система множин R є кільцем, якщо:

1) вона замкнена відносно операцій ;

2) вона замкнена відносно операцій ;

3) - деяке відображення, R₁ - деяке кільце множин з , і RR₁;

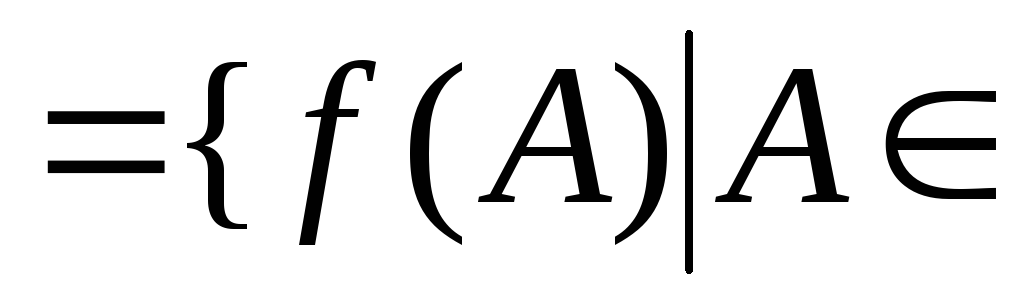4) RR₁R₂, де R₁, R₂ - кільця;

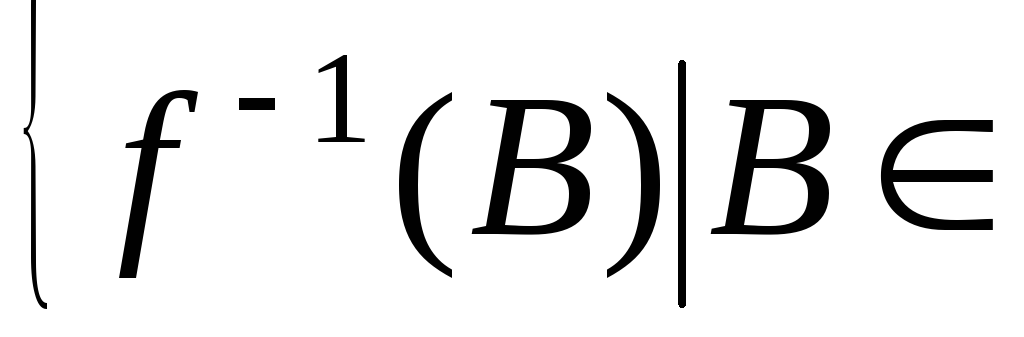б) - деяке відображення, - система підмножин , тоді RR, де через R позначено кільце, породжене множиною ;

в) для деякого відображення сукупність R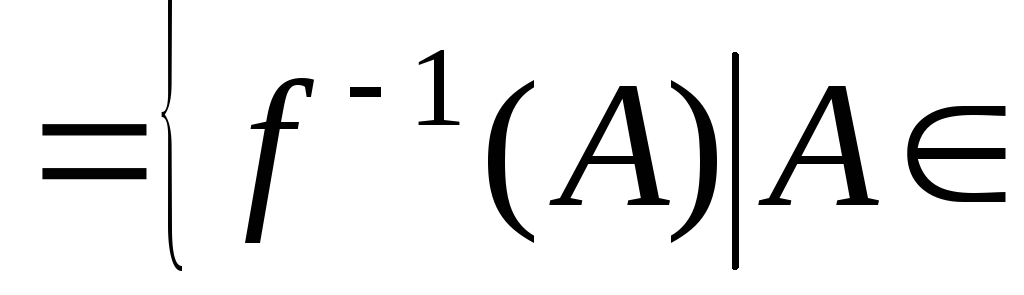R₁ підмножин є:

1) півкільцем, якщо R₁ - півкільце підмножин ;

2) кільцем, якщо R₁ - кільце підмножин ;

3) алгеброю, якщо R₁ - алгебра підмножин ;

4) кільцем, якщо R₁ - кільце підмножин ;

5) алгеброю, якщо R₁ - алгебра підмножин ;

г) система множин A є алгеброю, якщо:

1) A A₁ A₂, де A₁, A₂ - алгебри;

2) AA, де A- алгебра;

д) декартів добуток двох кілець є кільцем;

е) декартів добуток двох півкілець є півкільцем;

6. Побудувати:

а) , де:

1) множиною є множина усіх раціональних чисел із знаменником , тобто ;

2) , якщо - довільна послідовність усіх раціональних чисел з проміжку ;

а) породжене кільце R, де:

1) , де - деяка множина;

2) , де - деякі множини;

3) ;

б) для найменшу алгебру, що містить як елементи множини:

1) ;

2) ;

7. Навести приклад:

а) послідовності множин , для якої в задачі 1 б) усі три включення є строгими;

б) кільця множин:

1) що не є ні алгеброю, ні кільцем;

2) що не є кільцем, але замкнене відносно операції зліченого перетину;

в) для основного простору :

1) півкільця, що не є кільцем;

2) кільця множин, що не є ні алгеброю;