
Lektsii_Rubleva_1 / Гл 07 _нтеграли залежн_ в_д параметра / Пар 7-1 Невласн_ _нтеграли
.doc
Глава 7
Інтеграли, залежні від параметра
1. Невласні інтеграли
Нехай
![]() і
і
![]()
![]() .
Тоді визначено функцію
.
Тоді визначено функцію
![]() ,
де
,
де
|
|
|
(1) |
Якщо
існує
![]() ,
то
,
то
![]() називається інтегрованою
за Ріманом на проміжку
називається інтегрованою
за Ріманом на проміжку
![]() (в невласному розумінні), а число
(в невласному розумінні), а число
![]() її
невласним інтегралом першого ряду.
При цьому позначають
її
невласним інтегралом першого ряду.
При цьому позначають
|
|
|
(2) |
Якщо вказана границя не існує, або дорівнює нескінченності, то кажуть, що відповідний невласний не існує, чи розбігається.
Повністю
аналогічно, для функції
![]() ,
якщо
,
якщо
![]()
![]() і існує
і існує
![]()
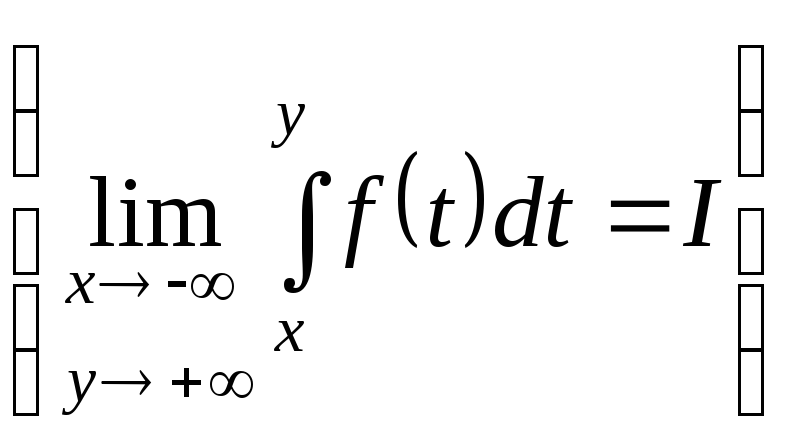 ,
то
,
то
![]()
![]() .
.
|
Приклад 1. |
|
|
|
Розглянемо
функцію (1)
|
|
Теорема 1. |
(Еквівалентні умови збіжності) |
|
|
Нехай
|
|
1) |
|
|
2) |
|
|
3) |
|
|
4) |
|
Доведення.
1) означає, що
![]()
![]() збігається
збігається
![]()
![]() для функції
для функції
![]() виконується критерій Коші
виконується критерій Коші
![]() 2)
2)
![]()
![]() має границю у розумінні Гейне
має границю у розумінні Гейне
![]() 3)
3)
![]() через зв’язок між рядами та послідовностями
через зв’язок між рядами та послідовностями
![]() 4). Якщо збігається ряд в умові 4)
4). Якщо збігається ряд в умові 4)
![]()
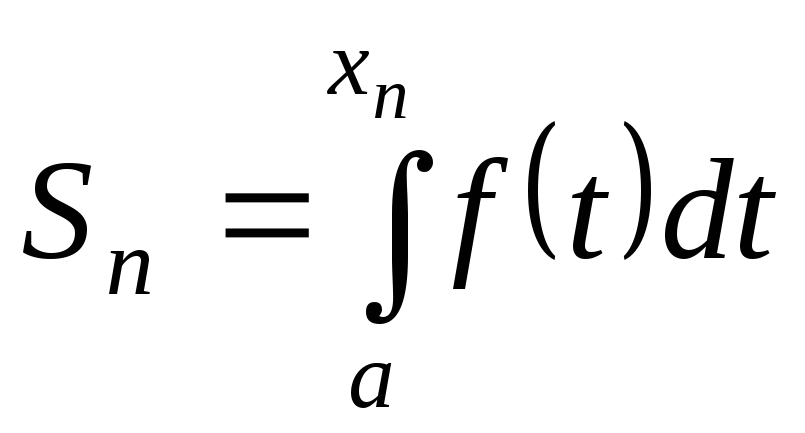 -
збіжна,
-
збіжна,
![]() існує
існує
![]() ,
тобто справджується 1).
,
тобто справджується 1).
Теорема доведена.
|
Приклад 2. |
Суттєва
є довільність
|
Нехай
![]() невід’ємна обмежена функція, неперервна
невід’ємна обмежена функція, неперервна
![]() ,
за винятком можливо множини лебегової
міри нуль. Це означає, що: 1)
,
за винятком можливо множини лебегової
міри нуль. Це означає, що: 1)
![]()
![]() ;
2)
;
2)
![]() неперервна
для такої функції
неперервна
для такої функції
![]() ;
3)
;
3)
![]() неспадна функція
неспадна функція
![]() існування
існування
![]() еквівалентно її обмеженості (аналогічно
теорії знакосталих рядів).
еквівалентно її обмеженості (аналогічно
теорії знакосталих рядів).
|
Теорема 2. |
(Ознака порівняння) |
|
|
Нехай
функції
|
Доведення.
![]() маємо:
маємо:
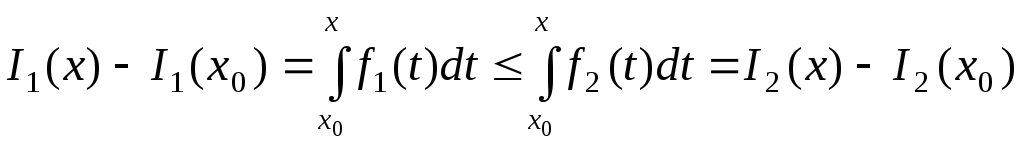
![]() слідує все що треба.
слідує все що треба.
Теорема доведена.
|
Наслідок 1. |
(Інтегральна ознака збіжності числового ряду) |
|
|
Нехай
невід’ємна функція
|
Доведення.
З теореми 1 із збіжності інтегралу слідує
збіжність ряду для будь-якої послідовності
![]() ,
таким чином необхідність доведена. Для
доведення достатності використаємо
умову невід’ємності функції
,
таким чином необхідність доведена. Для
доведення достатності використаємо
умову невід’ємності функції
![]() .
.
![]()
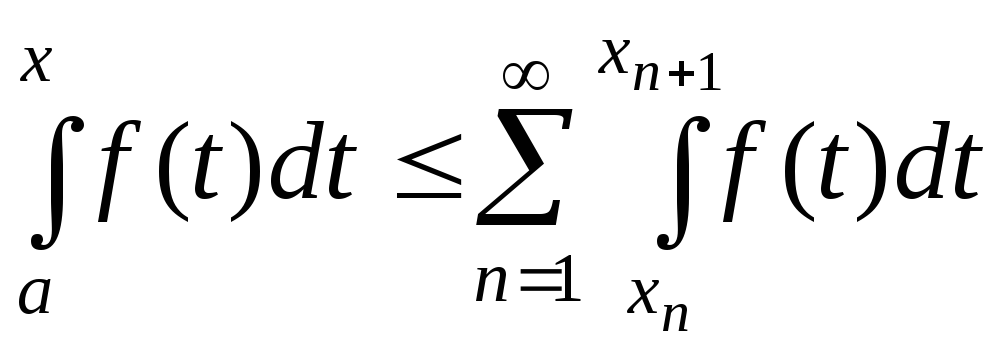 ,
а тому
,
а тому
![]() - монотонна й обмежена, з чого і слідує,
що
- монотонна й обмежена, з чого і слідує,
що
![]() - збіжний.
- збіжний.
Теорема доведена.
|
Наслідок 2. |
(Інтегральна ознака Коші збіжності числового ряду) |
|
|
Нехай
невід’ємна не зростаюча функція
|
Доведення.
Покладемо в умовах наслідку 1 послідовність
![]() .
Тоді розглянемо такі часткові суми:
.
Тоді розглянемо такі часткові суми:
![]() та
та
![]() .
Для них ми можемо записати такі
співвідношення (з урахування неспадності
функції
.
Для них ми можемо записати такі
співвідношення (з урахування неспадності
функції
![]() ):
):
![]() ,
,
![]() ,
,
з яких слідує, що ряди збігаються чи розбігаються одночасно. А далі все слідує з першого наслідку.
Наслідок доведено.
Якщо
для функції
![]() збігається інтеграл
збігається інтеграл
![]() ,
то
,
то
![]() називається абсолютно
збіжним.
Не абсолютно збіжний інтеграл називається
умовно
збіжним.
називається абсолютно
збіжним.
Не абсолютно збіжний інтеграл називається
умовно
збіжним.
|
Теорема 3. |
(Зв’язок абсолютної та умовної збіжності інтегралу) |
|
|
Якщо
|
Доведення.
Використаємо критерій Коші. Все слідує
з умови
![]()
![]() та нерівності
та нерівності
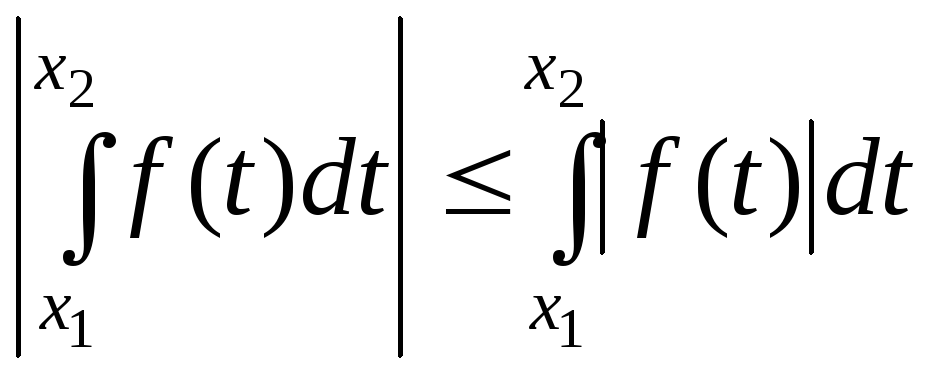 .
.
|
Теорема 4. |
(Інтегрування частинами невласного інтегралу) |
|
|
Нехай
функції
|
Доведення.
Все слідує з аналогічної формули для
інтегралу Рімана (власного) інтегралу:
 .
Далі граничний перехід при
.
Далі граничний перехід при
![]() .
.
Теорема доведена.
|
Теорема 5. |
(Заміна змінної в невласному інтегралі) |
|
|
Нехай
функція
|
Доведення.
Ця теорема також є наслідком аналогічної
властивості для інтегралу Рімана.
![]()
![]() :
:
![]() ,
де
,
де
![]() (внаслідок неперервності та монотонності
функції
(внаслідок неперервності та монотонності
функції
![]() )
)
![]()
![]() ,
ну а далі граничний перехід при одночасному
прямуванні
,
ну а далі граничний перехід при одночасному
прямуванні
![]() до нескінченності.
до нескінченності.
Теорема доведена.
|
Теорема 6. |
(Лінійність невласного інтегралу) |
|
|
Якщо
існують інтеграли
|
|
Теорема 7. |
(Практична ознака збіжності) |
|
|
Нехай
Якщо
існують такі сталі
Якщо
існують такі сталі
|
Все це слідує з порівняння відповідного інтегралу із степеневим.
|
Приклад 3. |
Дослідити
на збіжність:
|
|
|
|
|
Теорема 8. |
(Ознака Абеля) |
|
|
Нехай
функції
|
Доведення.
За другою теоремою про середнє внаслідок
монотонності функції
![]() можемо записати рівність
можемо записати рівність
![]()
 .
Якщо записати критерій Коші збіжності
інтегралу
.
Якщо записати критерій Коші збіжності
інтегралу
![]() ,
то
,
то
![]()
![]()
![]()
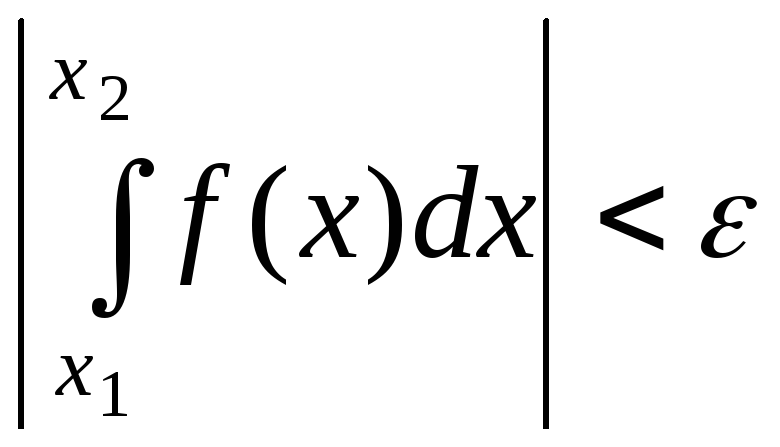 ,
а тому
,
а тому
![]() .
.
Теорема доведена.
|
Теорема 9. |
(Ознака Діріхле) |
|
|
Нехай
функції
|
Доведення.
За другою теоремою про середнє внаслідок
монотонності функції
![]() можемо записати рівність
можемо записати рівність
![]()
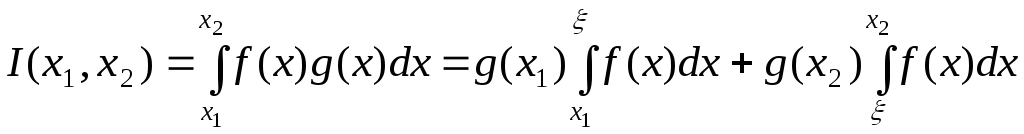 .
Якщо записати критерій Коші збіжності
функції
.
Якщо записати критерій Коші збіжності
функції
![]() до нуля, то
до нуля, то
![]()
![]()
![]()
![]() ,
а тому
,
а тому
![]() .
.
Теорема доведена.
|
Приклад 4. |
Дослідити
на абсолютну та умовну збіжність:
|
|
|
1)
2)
а)
2)
б)
3)
При
|
Нехай
![]() і інтеграл
і інтеграл
![]() - розбіжний. Якщо при цьому існує
- розбіжний. Якщо при цьому існує
![]() ,
то цю границю називають головним
значенням у розумінні Коші
розбіжного інтеграла і позначають
,
то цю границю називають головним
значенням у розумінні Коші
розбіжного інтеграла і позначають
![]()
|
Приклад 5. |
Знайти
головне значення у розумінні Коші
інтеграла для функції
|
|
|
|

 ,
при
,
при
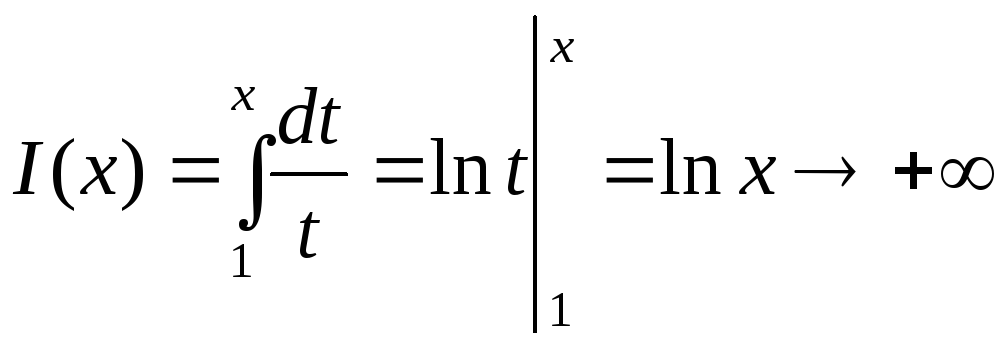 .
. ;
;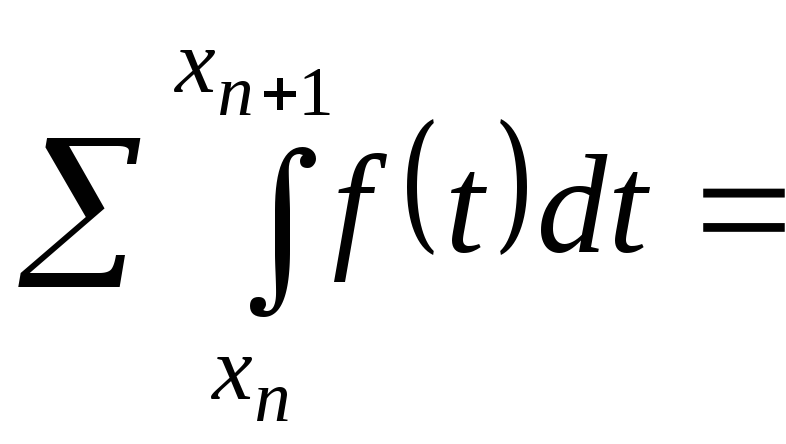
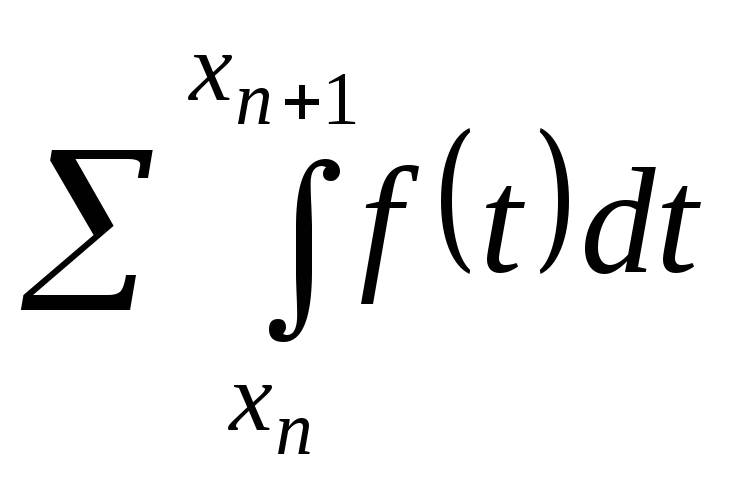 - збіжний.
- збіжний.