Lektsii_Rubleva_1 / Гл 11 М_ра Лебега / Пар 11-1 Вим_рн_ функц_ї

Глава 11

Вимірні функції. Інтеграл Лебега

1. Вимірні функції

Простір з мірою – це вимірний простір A, в якому на алгебрі A визначена міра . Його позначають трійкою A, але частіше ми його будемо позначати як і раніше буквою . В подальшому ми будемо вивчати функції, що визначені на вимірному просторі.

Нехай A та A₁ - вимірні простори, нехай задана функція . Її називають вимірною функцією, якщо прообраз будь-якої A₁-вимірної множини A-вимірний, тобто A₁ її прообраз A.

Зрозуміло, що нас будуть цікавити в основному числові вимірні функції, тому в подальшому будемо вважати, що . Будемо вважати в вимірними борелевські множини. Тоді вимірність функції (ВФ) означає, що для будь-якої борелевської множини його прообраз вимірний, тобто A. Якщо функція визначена на алгебрі борелевських множин B, то вона називається вимірною за Борелем, а якщо на алгебрі лебегівських множин - вимірною за Лебегом.

Позначимо через множину , аналогічно для інших типів нерівностей.

Теорема 1.	(Критерій вимірності функції)
	Функція - вимірна тоді і тільки тоді, коли множина - вимірна.

Доведення. Необхідність. Зрозуміло, що множина - борелевська, а тому її прообраз, тобто множина - відкрита.

Достатність. Легко зрозуміти, що множини, прообрази яких вимірні, утворюють алгебру. Якщо множина - вимірна, то ми маємо (використовуючи властивості прообразів): 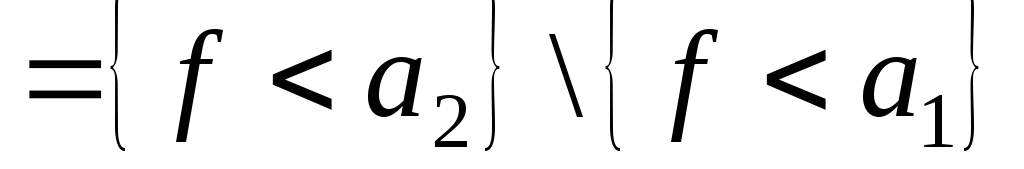- вимірна. Таким чином, система підмножин , прообрази яких вимірні, є алгеброю, що містить усі півінтервали вигляду , а тому містить усі борелевські множини.

Теорема доведена.

Теорема 2.	(Еквівалентний критерій вимірності функцій)
	Теорема 1 залишиться чинною, якщо множину замінити на будь-яку з множин , чи .

Доведення. Достатньо одержати такі рівності: ; .

Теорема доведена.

Лема 1.	(Вимірність характеристичної функції)
	Множина - вимірна - ВФ.

Доведення слідує з рівності: .

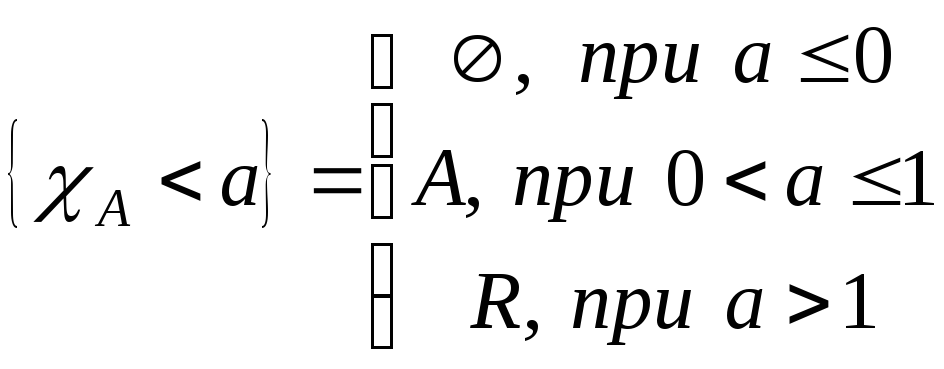Теорема 3.	(Вимірність неперервних функцій)
	Неперервна функція вимірна за Борелем.

Доведення. Для неперервної функції прообраз відкритої множини відкритий, тому множина - відкрита.

Теорема доведена.

Теорема 4.	(Вимірність композиції)
	Якщо ВФ. Тоді - ВФ за Борелем їх композиція - ВФ.

Доведення. , де - вимірна за Борелем множина, а тому й її прообраз є вимірним, а тому й множина - вимірна, тобто - вимірна.

Теорема доведена.

Зауваження.

Для функцій вимірних за Лебегом твердження не вірне.

Теорема 5.	(Арифметичні дії з ВФ)
	Якщо - ВФ, , то наступні функції вимірні: , , , , , , (якщо ), , .

Доведення.

1) .

2) При - очевидно, інакше: .

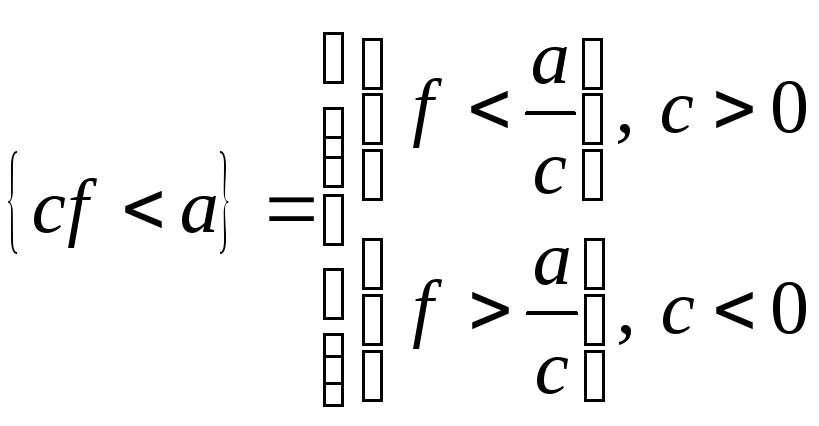3) .

4) .

5) Нехай - послідовність усіх раціональних чисел, тоді .

6) .

7) , доведемо, що - ВФ. .

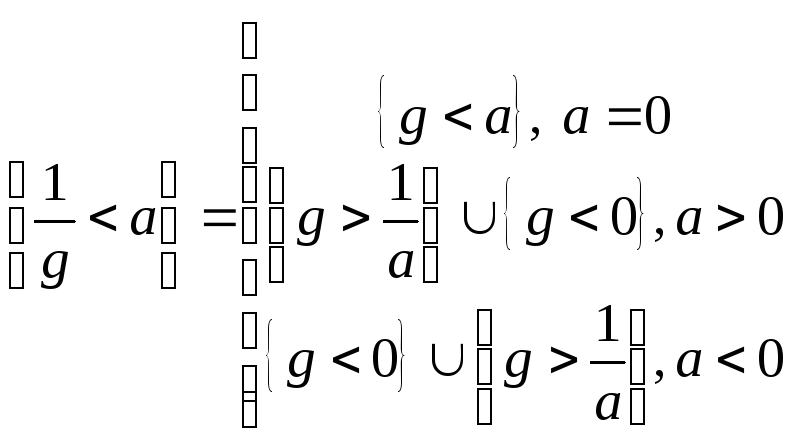8) , .

Теорема доведена.

Теорема 6.	(Вимірність границі)
	Нехай - ВФ, , тоді - ВФ.

Доведення. . З цієї рівності усе слідує. Доведемо її. (лівій частині) належить правій частині. Навпаки, якщо належить правій частині, то , а тому при , одержимо , тобто належить лівій частині.

Теорема доведена.